这个领域的背景

相关性质

QDFT和IQDFT的公式：
$$\begin{gathered} F(u,v)=\frac{1}{M}\sum _{x=0}^{M-1}\sum _{y=0}^{M-1}{e}^{-2\mu \pi (\frac{ux}{M}+\frac{vy}{M})}f(x,y) \\ f(x,y)=\frac{1}{M}\sum _{u=0}^{M-1}\sum _{v=0}^{M-1}{e}^{-2\mu \pi (\frac{ux}{M}+\frac{vy}{M})}f(u,v) \\ 注：如果是DFT的话将\mu 改为i即可 \end{gathered}$$

文章信息

1. 作者：Junlin Ouyang
2. 期刊：HAL
3. 题目：Robust hashing for image authentication using quaternion discrete Fourier transform and log-polar transform

目的、实验步骤及结论

1. 目的：使用对数极坐标来抗旋转，之后再用QDFT提取特征。

2. 实验步骤

   • 数据预处理：先统一256*256的大小，再使用k * k的平均滤波器（窗口大小为7），最后将最大内切圆以外的像素置为0（黑色）。

   • 对数极坐标变换：对圆形的图像进行对数极坐标变换，形成二次图像。

   • QDFT：对二次图像进行QDFT，使用中心的p（15*15）个低频信号的系数，通过下述公式来生成哈希值，即比较前后两个低频信号的系数来生成哈希值。
     

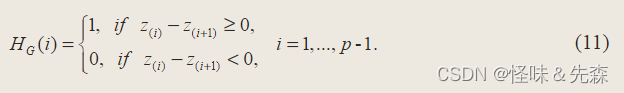
   • 相似性评价：使用汉明距离来判断两张图片是否一致，如果小于阈值则是一张图片。

3. 结论：

   这篇论文提供了一个抗旋转的小组件，也就是对数极坐标，这个针对于特定的算法能够很有效地提高康旋转的能力，同时在这篇论文中使用公式进行推导：旋转之后的图片使用对数极坐标+QDFT后形成的哈希值理论上完全一致。

在进行代码实现的时候，由于论文中并没有给出QDFT后的四元数矩阵系数的计算公式，但是可以直接使用二维快速傅里叶变换实现计算。实现代码如下：

def image_hash(img_path,k):
    img = processing(img_path)
    feature = image_feature(img)
    h_i = gen_hashing(feature,k)
    return h_i

def processing(img_path):
    """
    input：图片的路径
    output：处理后的RGB图片
    """
    try:
        img = cv2.imread(img_path)
        x = img.shape[0]//2 # 高度
        y = img.shape[1]//2 # 宽度
        Min = x if x<y else y
        cropped_image = img[x-Min:x+Min, y-Min:y+Min] # 裁剪图像
        img = cv2.resize((cropped_image), (256,256), interpolation=cv2.INTER_LINEAR)
    except:
        img = imageio.mimread(img_path)
        img = np.array(img)
        img = img[0]
        img = img[:, :, 0:3]
        x = img.shape[0]//2 # 高度
        y = img.shape[1]//2 # 宽度
        Min = x if x<y else y
        cropped_image = img[x-Min:x+Min, y-Min:y+Min] # 裁剪图像
        img = cv2.resize((cropped_image), (256,256), interpolation=cv2.INTER_LINEAR)
#     out = cv2.GaussianBlur(img, (3, 3),1.3) # 使用python自带的高斯低通滤波
    kernel = np.ones((7,7), np.float32) / 49 # 平均滤波器
    out = cv2.filter2D(img, -1 , kernel=kernel)  # 二维滤波器
    out = cv2.cvtColor(out, cv2.COLOR_BGR2RGB)
    out = square2circle(out)
    log_polar_img = cv2.logPolar(out, (out.shape[1] // 2, out.shape[0] // 2), 50, cv2.WARP_FILL_OUTLIERS)
    return log_polar_img

def square2circle(img):
    """
    将最大内切圆以外的像素值置为0
    img:array(512,512,3)
    return:array(512,512,3)
    """
    h,w,_ = img.shape
    radius = int(min(h, w) / 2)  
    mask = np.zeros((h, w,3), np.uint8)  
    # 在mask中画出一个最大半径为radius的圆形区域
    cv2.circle(mask, (w // 2, h // 2), radius, (255, 255, 255), -1)  
    # 对原图和mask进行位运算，将圆形区域外的像素设置为0  
    img_process = cv2.bitwise_and(img, mask)
    return img_process

def image_feature(img):
    """
    iamge:(512,512,3)
    return: array(512,512)
    """
    rows,cols,_ = img.shape
    quaternion_array = np.array([[np.quaternion(0, img[i,j,0],img[i,j,1],img[i,j,2]) for j in range(cols)] for i in range(rows)])
    return np.fft.fftshift(fft2D(quaternion_array))
    
def exp_quaternion(u):
    """
    四元数的指数运算
    """
    # 手动计算四元数的模，并用它来规范化四元数
    norm_u = np.abs(u)
    v = u / (norm_u+(1e-80))
    # 计算指数形式的指数运算
    exponential_form = np.cos(norm_u) + v * np.sin(norm_u)
    return exponential_form

def fft1D(signal):
    """
    signal:为一维的四元数序列
    return:*
    """
    # 定义单位纯四元数 u = ai + bj + ck，其中 |u| = 1
    # 构建单位纯四元数
    # 第一种四元数论文常用单位四元数
    d1=3**(1/2)
    u_lum = qt.quaternion(0, 1/d1, 1/d1, 1/d1)
    # 第二种单位四元数
    d2=68**(1/2)
    u_perc=qt.quaternion(0, 0, -2/d2, 8/d2)
    N = len(signal)
    if N <= 1:
        return signal
    even = fft1D(signal[0::2])
    odd = fft1D(signal[1::2])
    #一维傅里叶变换公式
    T = [exp_quaternion(-2*u_lum * np.pi * k / N) * odd[k] for k in range(N // 2)]
    # T = [exp_quaternion(-2 * u_perc * np.pi * k / N) * odd[k] for k in range(N // 2)]
    return np.concatenate([even + T, even - T])
    
def fft2D(image):
    """
    image:四元数矩阵(256*256)
    return:返回经过傅里叶变换后的四元数矩阵
    """
    M, N = image.shape
    if M <= 1 and N <= 1:
        return image
    # FFT along rows
    rows = np.array([fft1D(row) for row in image])
    # FFT along columns
    cols = np.array([fft1D(col) for col in rows.T]).T
    return cols

def gen_hashing(feature_matrix,k):
    """
    选取振幅系数矩阵中间偏左上的矩阵作为特征。
    input:array (256,256)
    output:list (x)
    """
    coeff = []
    start = int(feature_matrix.shape[0]/2-k//2+1)
    for i in range(start,start+k):
        for j in range(start,start+k):
            coeff.append(feature_matrix[i][j].abs())
    return np.array([1 if coeff[i] >= coeff[i+1] else 0 for i in range(len(coeff)-1)])
    
def dist_img(h1,h2):
    return sum(np.abs(h1-h2))/len(h1)