文章目录
- 题目一:最大子数组和(No. 53)
- 题解
- 题目二:合并区间(No. 56)
- 题解
- 题目三:轮转数组(No. 189)
- 题解
- 题目四:除自身以外数组的乘积(No. 238)
- 题解
- 题目五:缺失的第一个正数(No. 41)
- 题解
题目一:最大子数组和(No. 53)
题目链接:https://leetcode.cn/problems/maximum-subarray/description/?envType=study-plan-v2&envId=top-100-liked
题目难度:中等
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
**子数组:**是数组中的一个连续部分。
示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
示例 2:
输入:nums = [1]
输出:1
示例 3:
输入:nums = [5,4,-1,7,8]
输出:23
提示:
1 <= nums.length <= 105104 <= nums[i] <= 104
题解
**前缀和:**假设有一个数组 [a1, a2, a3, a4, a5, a6]
- 前缀和 prefix[1] 为 a1
- 前缀和 prefix[2] 为 a1 + a2
- 前缀和 prefix[3] 为 a1 + a2 + a3
- 前缀和 prefix[4] 为 a1 + a2 + a3 + a4
- 前缀和 prefix[5] 为 a1 + a2 + a3 + a4 + a5
- 前缀和 prefix[6] 为 a1 + a2 + a3 + a4 + a5 + a6
通过前缀和,**可以很轻松的去求得一个连续子数组的和:**比如 a3 到 a6 到数组和就可以通过 prefix[6] - prefix[3] 来计算得出。
以 an(1 < n < prefix.length) 结尾的子数组的和最大的时候,就是 prefix[n] 减去 前面出现过的最小的前缀和 或者 就是这个前缀和本身,将这两个结果取一个最大值,就是以这个节点结尾的子数组最大的和。
通过上面的分析, 本题需要这几个变量:一个 prefix 数组、存储结果的 res,存储此时最小的前缀和的 minPre;当遍历到一个节点的时候,比较以下的三个变量:
- res、prefix[i]、prefix[i] - minPre
当遍历完成后,就能得到最终的结果。
class Solution {
public int maxSubArray(int[] nums) {
int temp = 0;
int[] prefix = new int[nums.length];
for (int i = 0; i < nums.length; i++) {
temp += nums[i];
prefix[i] = temp;
}
int minPre = prefix[0];
int res = prefix[0];
for (int i = 1; i < prefix.length; i++) {
res = Math.max(prefix[i] - minPre, res);
res = Math.max(prefix[i], res);
minPre = Math.min(minPre, prefix[i]);
}
return res;
}
}
题目二:合并区间(No. 56)
题目链接:https://leetcode.cn/problems/merge-intervals/?envType=study-plan-v2&envId=top-100-liked
题目难度:中等
以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。
示例 1:
输入:intervals = [[1,3],[2,6],[8,10],[15,18]]
输出:[[1,6],[8,10],[15,18]]
解释:区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
示例 2:
输入:intervals = [[1,4],[4,5]]
输出:[[1,5]]
解释:区间 [1,4] 和 [4,5] 可被视为重叠区间。
提示:
1 <= intervals.length <= 104intervals[i].length == 20 <= starti <= endi <= 104
题解
一个区间由左右区间来限定,即 [left, right],要判断两个区间能否合并需要两个条件
- left1 ≤ left2
- right1 ≥ left2
但是这样的判定方式显然不适合解题,因为要查找一个区间能和几个区间合并的时候,每次都需要去遍历整个数组。
但如果按照 left 的大小来进行排序,就可以减少一个判断的条件,经过排序后,前后两个区间一定满足 left1 ≤ left 所以只需要去判断右边界即可
- 当右边界大于下一个区间的左边界的时候,这两个区间就可以合并了。
- 但如果发现右边界小于下一个区间的左边界,则区间就无法继续合并,就需要开辟一个新的区间来继续执行合并的流程。
通过上面的分析,本题需要这些变量:目前遍历区间的左边界 currentLeft,有边界 currentRight,存储结果的集合 resList。
本题的思路遍历数组,寻找下一个区间能否和本次的区间 [currentLeft, currentRight] 合并,如果可以,就更新 currentRight,否则将当前区间添加到结果数组中,然后继续遍历。
class Solution {
public int[][] merge(int[][] intervals) {
if (intervals.length <= 1) return intervals;
// 收集结果的集合
List<int[]> resList = new ArrayList<>();
// 按照起点的顺序排序
Arrays.sort(intervals, (x, y) -> Integer.compare(x[0], y[0]));
int currentLeft = intervals[0][0];
int currentRight = intervals[0][1];
for (int i = 1; i < intervals.length; i++) {
if (intervals[i][0] > currentRight) {
// 前一个范围无法覆盖到这个内容
resList.add(new int[]{currentLeft, currentRight});
currentLeft = intervals[i][0];
currentRight = intervals[i][1];
} else {
// 可以覆盖的情况
currentRight = Math.max(intervals[i][1], currentRight) ;
}
}
// 最后一个区间没有添加到结果中,需要额外添加一次
resList.add(new int[]{currentLeft, currentRight});
return resList.toArray(new int[resList.size()][]);
}
}
题目三:轮转数组(No. 189)
题目链接:https://leetcode.cn/problems/rotate-array/description/?envType=study-plan-v2&envId=top-100-liked
题目难度:中等
给定一个整数数组 nums,将数组中的元素向右轮转 k **个位置,其中 k **是非负数。
示例 1:
输入: nums = [1,2,3,4,5,6,7], k = 3
输出:[5,6,7,1,2,3,4]解释:
向右轮转 1 步:[7,1,2,3,4,5,6]
向右轮转 2 步:[6,7,1,2,3,4,5]
向右轮转 3 步:[5,6,7,1,2,3,4]
示例 2:
输入:nums = [-1,-100,3,99], k = 2
输出:[3,99,-1,-100]
解释:
向右轮转 1 步: [99,-1,-100,3]
向右轮转 2 步: [3,99,-1,-100]
提示:
1 <= nums.length <= 105231 <= nums[i] <= 231 - 10 <= k <= 105
题解
设数组的长度为 l,那轮转 l 次,得到的结果和原数组是完全相同的,假如轮转 k 次,其有效的轮转次数其实就是 k 对 l 取余数,也就是 k % l 次。
当轮转 m 次后,最终得到的结果就是数组的 后 m 个 元素到了新数组的开头,而 0 到这个位置的元素向后移动 m 位。
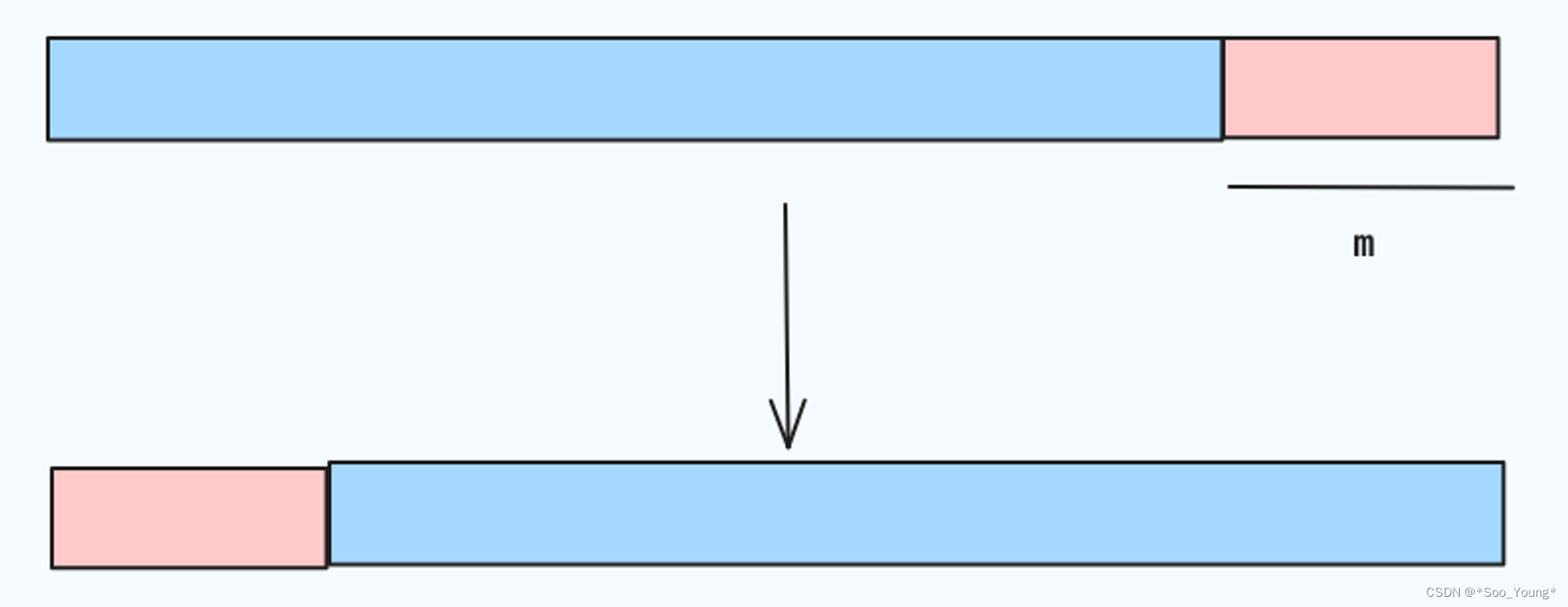
那第一个思路就很简单了,首先创造一个新的数组,然后对于原数组先从 length - m 遍历到末尾,然后再遍历 0 到 length - m - 1 这部分的内容,将这些内容填充到新的数组中。
再将新数组中的内容转移到旧数组中即可。
class Solution {
public void rotate(int[] nums, int k) {
int l = nums.length;
int realK = k % l; // 移动 l 的整数倍不会产生效果
int[] res = new int[l];
int newStart = nums.length - realK;
int temp = 0;
for (int i = newStart; i < nums.length; i++) res[temp++] = nums[i];
for (int i = 0; i < newStart; i++) res[temp++] = nums[i];
for (int i = 0; i < res.length; i++) nums[i] = res[i];
}
}
第二种思路就是反转数组,比如数组 1 2 3 4 5 6 7,要轮转 3 位置,那最终需要得到的数字就是这样的:5 6 7 1 2 3 4
要达到这样的效果,只需要先将数组翻转:7 6 5 4 3 2 1
然后翻转前 k 位:5 6 7 4 3 2 1
然后翻转后面的部分:5 6 7 1 2 3 4
只需要经过三次翻转就可以得到最终的结果。
class Solution {
public void rotate(int[] nums, int k) {
int realK = k % nums.length;
reverse(nums, 0, nums.length - 1);
reverse(nums, 0, realK - 1);
reverse(nums, realK, nums.length - 1);
}
public void reverse(int[] nums, int start, int end) {
while (start < end) {
int temp = nums[start];
nums[start] = nums[end];
nums[end] = temp;
start++;
end--;
}
}
}
题目四:除自身以外数组的乘积(No. 238)
题目链接:https://leetcode.cn/problems/product-of-array-except-self/description/?envType=study-plan-v2&envId=top-100-liked
题目难度:中等
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。
题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。
请 **不要使用除法,**且在 O(*n*) 时间复杂度内完成此题。
示例 1:
输入: nums =[1,2,3,4]输出:[24,12,8,6]
示例 2:
输入: nums = [-1,1,0,-3,3]
输出: [0,0,9,0,0]
提示:
2 <= nums.length <= 10530 <= nums[i] <= 30- 保证 数组
nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内
题解
如果不考虑 0 的情况下,本题的思路其实是比较容易的,就是先计算出整个数组的乘积,然后遍历到数组中的某个元素的时候,用这个乘积去除以这个元素,得到的结果放到 answer 数组中。
但是当出现 0 的情况就需要进行特殊的处理了,出现 0 的情况也分为两种情况
- 仅有一个 0 的情况
- 出现了两个及以上的 0 的情况
仅有一个零的情况也比较容易处理,比如题目中的案例二:
输入: nums = [-1,1,0,-3,3]
输出: [0,0,9,0,0]
其实规律也比较明显,为 0 的位置上的存储的是整个数组的乘积(除零以外),其他位置存储的全为 0。
当时当出现两个或者以上 0 的时候,结果数组中就全为 0 了。
所以本题的思路就是:先去遍历数组求出乘积(除零以外),同时统计 0 的个数,对没有 0,有一个 0 和有多个 0 的情况分别进行处理。
class Solution {
public int[] productExceptSelf(int[] nums) {
int zeroNum = 0;
int mulNum = 1;
int zeroIndex = 0; // 为 0 的位置的下标
int[] res = new int[nums.length];
for (int i = 0; i < nums.length; i++) {
if (nums[i] == 0) {
zeroNum++;
zeroIndex = i;
} else mulNum *= nums[i]; // 计算乘积
}
if (zeroNum > 1) return res;
else {
if (zeroNum == 1) {
res[zeroIndex] = mulNum;
return res;
} else {
for (int i = 0; i < nums.length; i++) res[i] = mulNum / nums[i];
}
}
return res;
}
}
题目五:缺失的第一个正数(No. 41)
题目链接:https://leetcode.cn/problems/first-missing-positive/description/?envType=study-plan-v2&envId=top-100-liked
题目难度:困难
给你一个未排序的整数数组 nums ,请你找出其中没有出现的最小的正整数。
请你实现时间复杂度为
O(n)
并且只使用常数级别额外空间的解决方案。
示例 1:
输入:nums = [1,2,0]
输出:3
解释:范围 [1,2] 中的数字都在数组中。
示例 2:
输入:nums = [3,4,-1,1]
输出:2
解释:1 在数组中,但 2 没有。
示例 3:
输入:nums = [7,8,9,11,12]
输出:1
解释:最小的正数 1 没有出现。
提示:
1 <= nums.length <= 105231 <= nums[i] <= 231 - 1
题解
本题的基础解法还是比较好想的,先将数组进行排列;定义一个 temp 变量,从 1 开始自增,遍历数组到正数部分的时候,就去判断数字和 temp 是否相等,不想等就直接返回 temp。
其中会有一个极端的情况,假如数组的长度为 N,而数组中的元素恰好就是 1 ~ N 中的所有元素,那此时最小的正数就是 N + 1;代码中 temp 是一直自增到结束的,所以当遍历结束后,如果还没有返回的话,此时 temp 存储的就是 N + 1 的值。
class Solution {
public int firstMissingPositive(int[] nums) {
Arrays.sort(nums); // 排序
int temp = 1;
// 对下标为 0 的情况进行特殊处理
if (nums[0] != temp && nums[0] > 0) return temp;
else if (nums[0] == temp) temp++;
for (int i = 1; i < nums.length; i++) {
if (nums[i] > 0) {
if (nums[i] == nums[i - 1]) continue; // 避免重复元素的干扰
if (temp != nums[i]) return temp; // 得到结果
else temp++;
}
}
return temp;
}
}
对于一个长度为 N 的数组,其所未包含的最小的正数,最大就是 N + 1,也就是上面提到的特殊情况,结果的范围其实就是 1 ~ N + 1;第二种方法就是对原数组进行操作,将每个元素在结果范围内的元素放到其对应位置上,然后再次遍历数组,找到位置不对的元素。
比如对案例 2 中的元素来说:[3, 4, -1, 1]
按照对应的位置排序完成是这样的:[1, -1, 3, 4]
处于 nums[i] 上的元素就是 i + 1,再次遍历发现不符合这种情况的就是最小的那个正数。
这个思路非常简单,就是对范围内的元素放到对应的位置上,然后再次遍历,但实现起来还是有很多地方需要注意的。
来梳理一下交换的条件:
- 首先 i 要在范围内,也就是 1 ≤ i ≤ nums.length
- 这个位置的元素要交换到 nums[nums[i] - 1] 的位置上去,要保证这个位置的元素不与 nums[i] 相等,如果相等就无需交换(其实还有避免死循环的因素,这个后面再说)。
写出来条件就是这样的:
nums[i] >= 1 && nums[i] <= nums.length && nums[i] != nums[nums[i] - 1]
那这个条件前面跟的是什么语句,if 还是 while 呢?
如果我们使用 if,交换了一个新的元素过来,此时去继续遍历下一个节点,那这个交换过来的新的元素是有效的元素的话,那这个元素就有可能未被处理到
比如案例 2,模拟一下使用 if 的情况:
原数组:[3, 4, -1, 1]
- 第一次交换:[-1, 4, 3, 1]
- 第二次交换:[-1, 1, 3, 4]
遍历结束,这里的问题就出现在第二次交换上,这里的 1 未被处理就直接放在了错误的位置上。
为了避免这样的情况,上面应该使用 while 来限制。
class Solution {
public int firstMissingPositive(int[] nums) {
for (int i = 0; i < nums.length; i++) {
// 排列数组
while (nums[i] >= 1 && nums[i] <= nums.length && nums[i] != nums[nums[i] - 1]) {
swap (nums, i, nums[i] - 1);
}
}
for (int i = 0; i < nums.length; i++) {
// 检测哪个位置是错误的
if (nums[i] != i + 1) return i + 1;
}
return nums.length + 1; // 如果都没问题,说明是特殊情况
}
// 交换节点的方法
void swap(int[] nums, int index1, int index2) {
int temp = nums[index1];
nums[index1] = nums[index2];
nums[index2] = temp;
}
}