C++进阶：搜索树

news2025/11/4 14:38:56

目录

  • 1. 二叉搜索树
    • 1.1 二叉搜索树的结构
    • 1.2 二叉搜索树的接口及其优点与不足
    • 1.3 二叉搜索树自实现
      • 1.3.1 二叉树结点结构
      • 1.3.2 查找
      • 1.3.3 插入
      • 1.3.4 删除
      • 1.3.5 中序遍历
  • 2. 二叉树进阶相关练习
    • 2.1 根据二叉树创建字符串
    • 2.2 二叉树的层序遍历I
    • 2.3 二叉树层序遍历II
    • 2.4 二叉树最近公共祖先结点
    • 2.5 二叉树搜索与双向链表
    • 2.6 从前序与中序遍历序列构造二叉树
    • 2.7 从中序与后序遍历序列构造二叉树
    • 2.8 二叉树前序遍历（非递归）
    • 2.9 二叉树中序遍历（非递归）
    • !!!3.10 二叉树后序遍历（非递归）

1. 二叉搜索树

1.1 二叉搜索树的结构

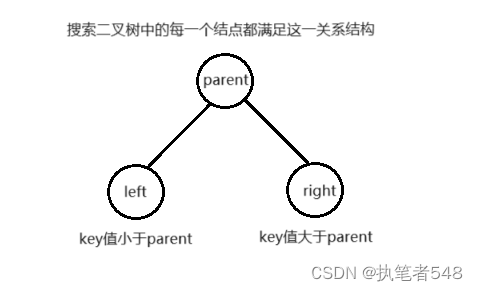
  1. 搜索二叉树中的所有结点都满足
    <1> 若左子树不为空，则其所有结点的键值都小于父结点
    <2> 若右子树不为空，则其所有结点的键值都大于父节点
    <3> 左右子树都为二叉搜索树

在这里插入图片描述

1.2 二叉搜索树的接口及其优点与不足

  1. 搜索二叉树的功能接口
    <1> 数据插入（Insert）
    <2> 数据删除（Erase）
    <3> 数据查寻（Find）
    <4> 中序遍历（InOrder）
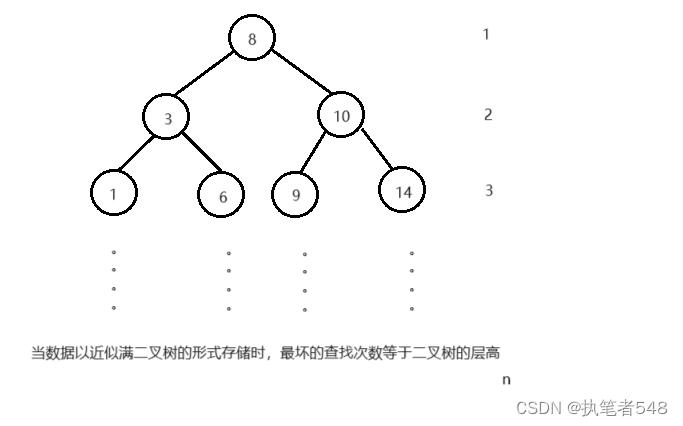
  1. 二叉搜索树的优点：
    <1> 正如其名，此种数据存储结构，尤其擅长数据搜索，其进行数据搜索的效率极高。
    <2> 在其结构为近似完全二叉树或满二叉树的情况时，其的搜索效率可以达到O( l o g N logN logN)
    <3> 当以中序遍历的方式遍历整棵搜索树时，得到的数据即为升序序列

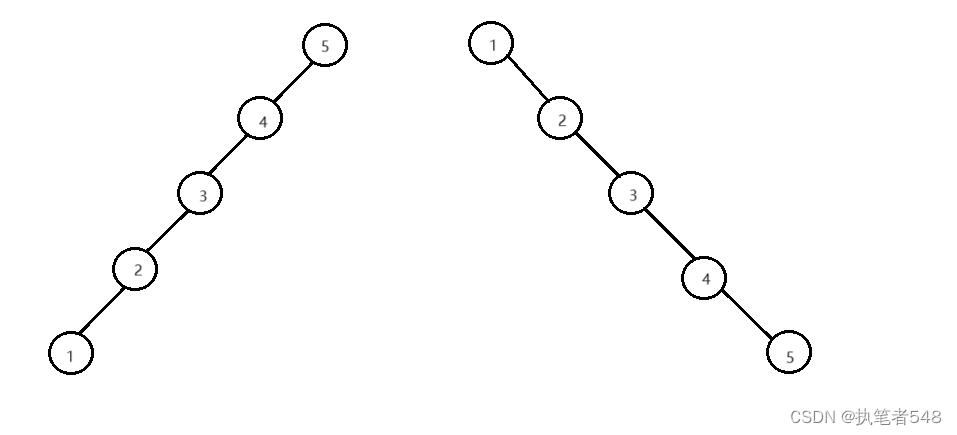
在这里插入图片描述

  1. 二叉搜索树的不足：
    <1> 根据二叉搜索树的插入逻辑，当数据以完全升序或降序插入时，会使得二叉树退化为单枝结构，此种结构下其搜索效率也退化为O(N)

在这里插入图片描述

1.3 二叉搜索树自实现

1.3.1 二叉树结点结构

  1. 搜索树结点：由左右孩子结点指针与key组成
  2. 搜索树：由根节点与类方法构成
template<class T>
struct BinarySearchNode
{
	typedef BinarySearchNode<T> BSNode;

	BSNode* _left;
	BSNode* _right;
	T _key;

	BinarySearchNode(T key)
		:_left(nullptr)
		,_right(nullptr)
		,_key(key)
	{}
};

template<class T>
class BinarySearchTree
{
public:
	typedef BinarySearchNode<T> BSNode;
	
	//查找
	bool Find(T key);

	//插入
	bool Insert(T key);

	//删除
	bool Erase(T key);

	//中序遍历
	void InOrder();

private:
	BSNode* _root = nullptr;
};

1.3.2 查找

  1. 查找实现：在一颗搜索树中搜寻一个数据是否存在
  2. 查找逻辑：
    <1> 若查找值小于当前结点的key值，向左搜寻，向左孩子查找
    <2> 若查找值大于当前结点的key值，向右搜寻，向右孩子查找
    <3> 查找遍历至空结点，则证明搜索树中不存在此值
//非递归
bool Find(T key)
{
	BSNode* cur = _root;

	while (cur)
	{
		if (key < cur->_key)
		{
			cur = cur->_left;
		}
		else if (key > cur->_key)
		{
			cur = cur->_right;
		}
		else
		{
			return true;
		}
	}

	return false;
}

//递归
bool _FindR(BSNode* cur, T key)
{
	if (cur == nullptr)
	{
		return false;
	}

	if (key < cur->_key)
	{
		return _FindR(cur->_left, key);
	}
	else if (key > cur->_key)
	{
		return _FindR(cur->_right, key);
	}
	else
	{
		return true;
	}

	//补全返回路径
	assert(true);
	return -1;
}

bool FindR(T key)
{
	return _FindR(_root, key);
}

1.3.3 插入

  1. 搜寻插入位置：
    <1> key小向左
    <2> key大向右
    <3> 直至遍历到空
  2. <1> 若遇key相同的结点，停止插入，返回false
    <2> 遍历至空，创建结点，链接结点
//非递归
bool Insert(T key)
{
	//特殊处理根结点插入
	if (_root == nullptr)
	{
		_root = new BSNode(key);
		return true;
	}

	BSNode* cur = _root;
	BSNode* parent = nullptr;
	while (cur)
	{
		if (key < cur->_key)
		{
			parent = cur;
			cur = cur->_left
		}
		else if (key > cur->_key)
		{
			parent = cur;
			cur = cur->_right;
		}
		else
		{
			return false;
		}
	}

	//确定插入位置
	if (key < parent->_key)
	{
		parent->_left = new BSNode(key);
	}
	else
	{
		parent->_right = new BSNode(key);
	}

	return true;
}

//递归
bool _InsertR(BSNode*& cur, T key)
{
	//存在单子树的情况，导致段错误
	//传引用
	if (cur == nullptr)
	{
		cur = new BSNode(key);

		return true;
	}

	if (key < cur->_key)
	{
		return _InsertR(cur->_left, key);
	}
	else if (key > cur->_key)
	{
		return _InsertR(cur->_right, key);
	}
	else
	{
		return false;
	}

	assert(true);
	return false;
}

bool InsertR(T key)
{
	if (_root == nullptr)
	{
		_root = new BSNode(key);
		
		return true;
	}

	return _InsertR(_root, key);
}

1.3.4 删除

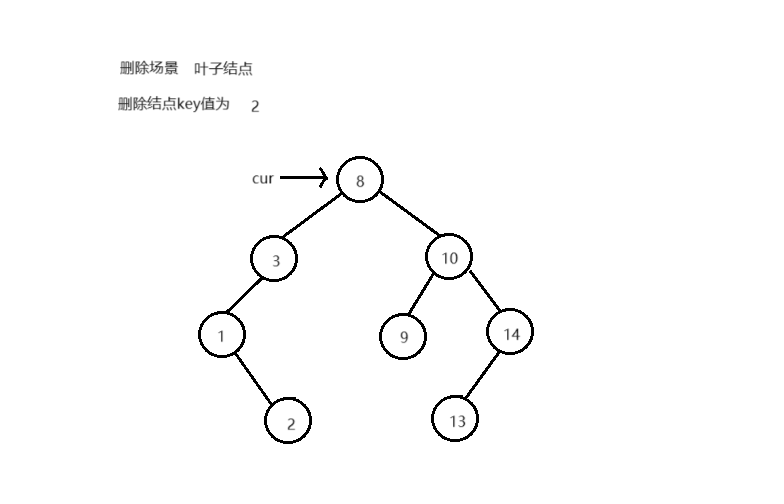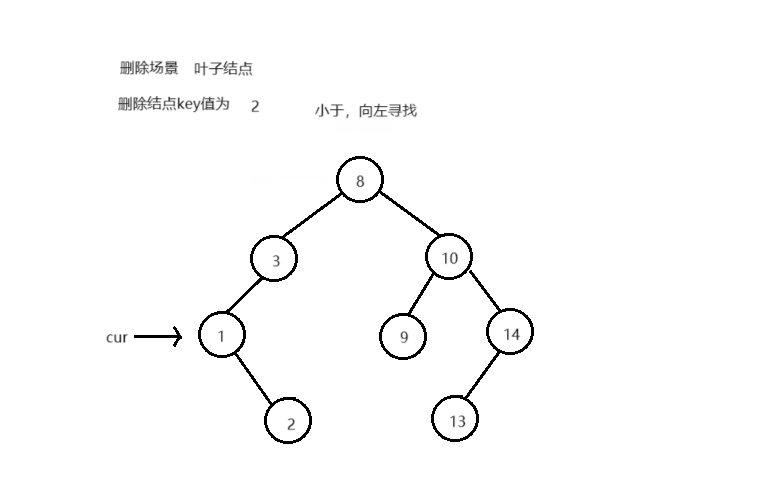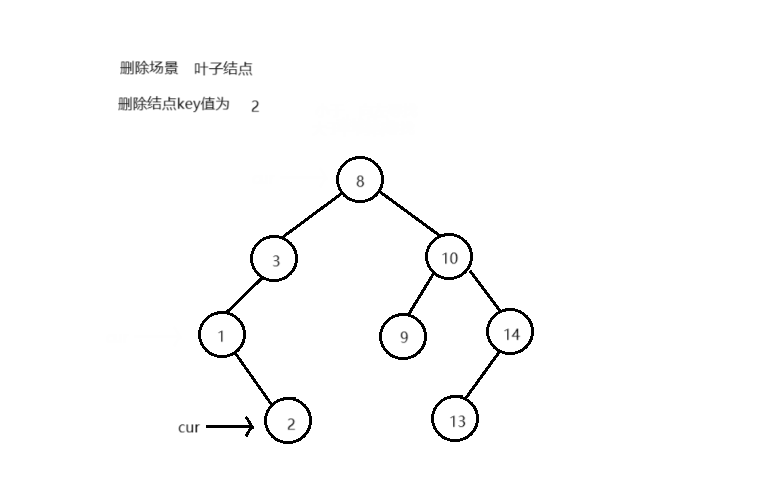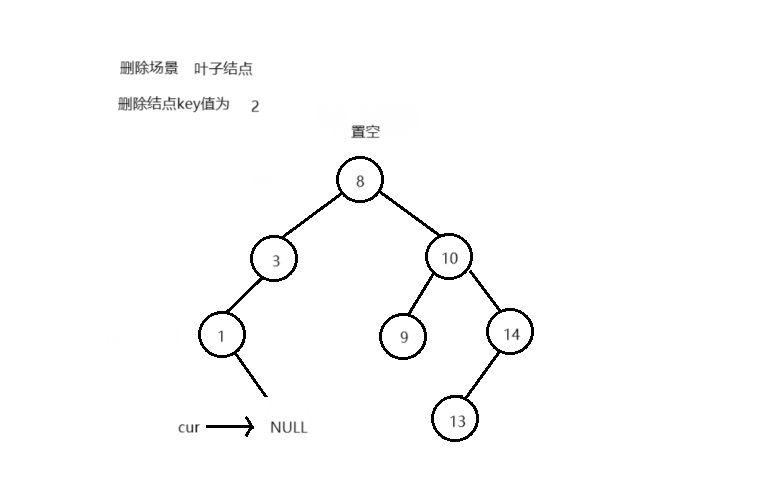
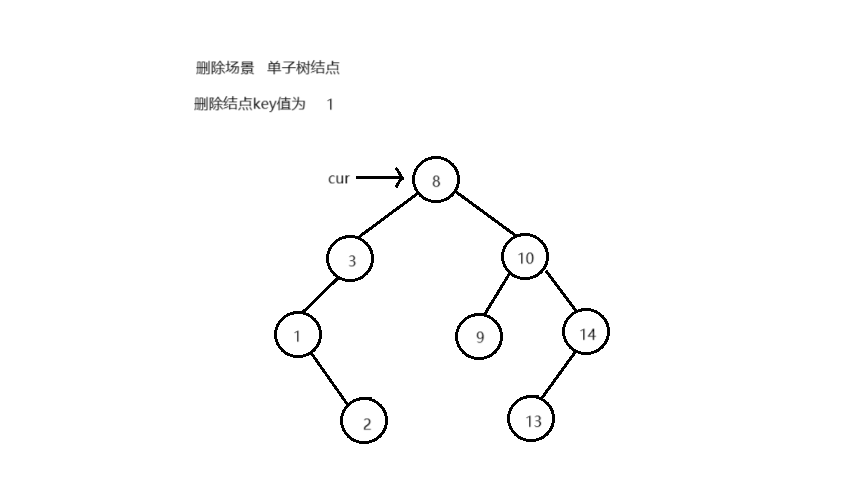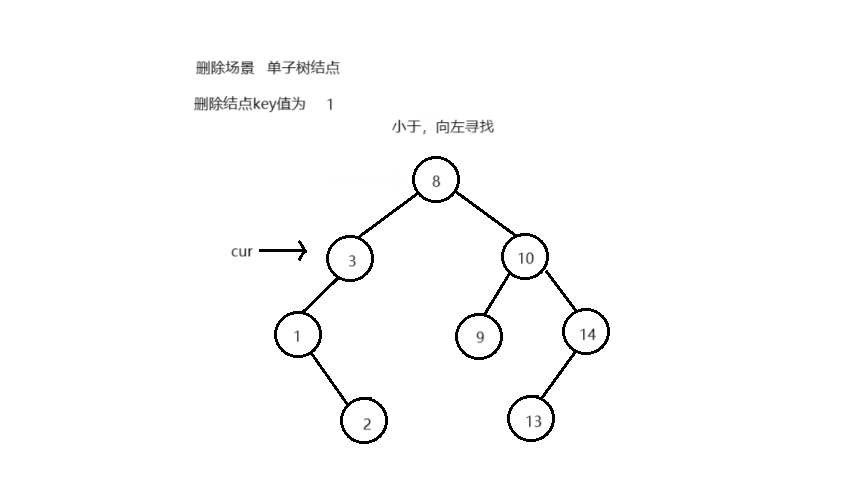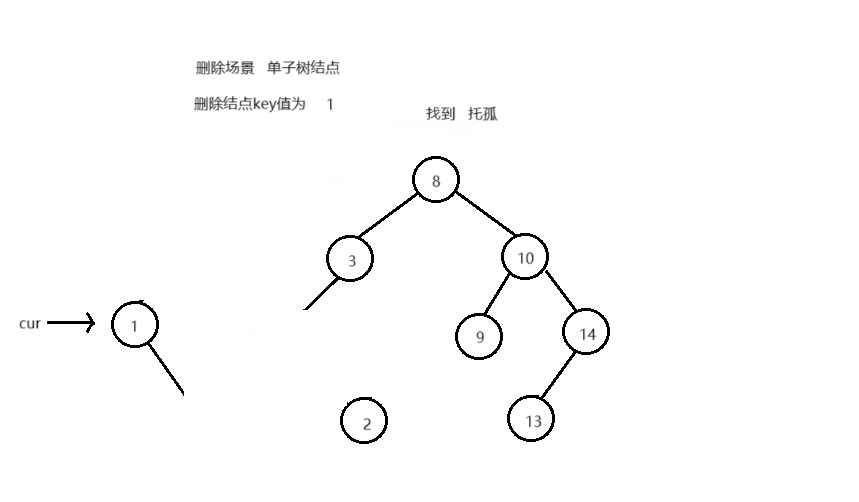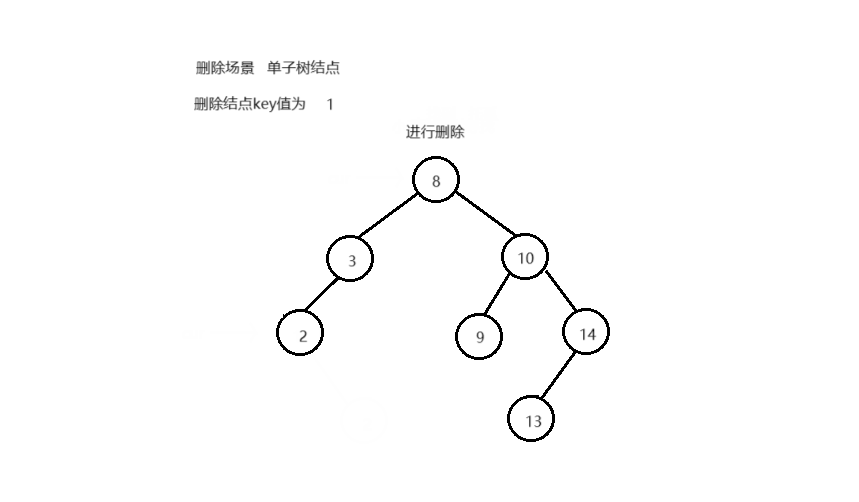
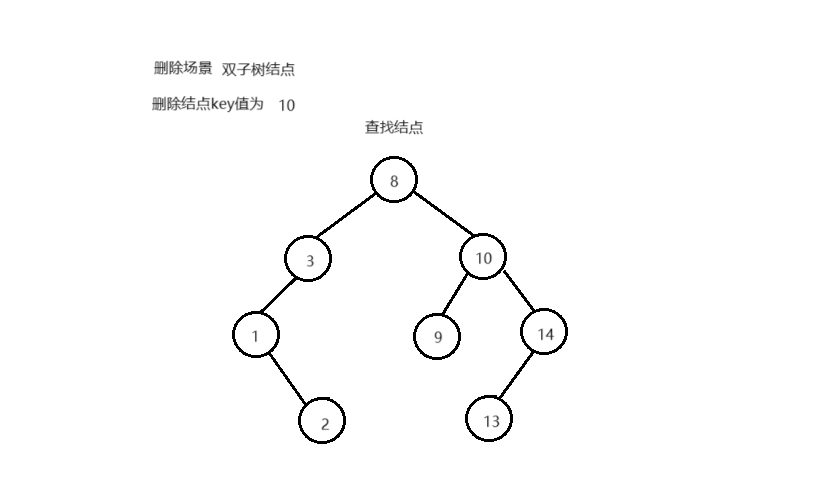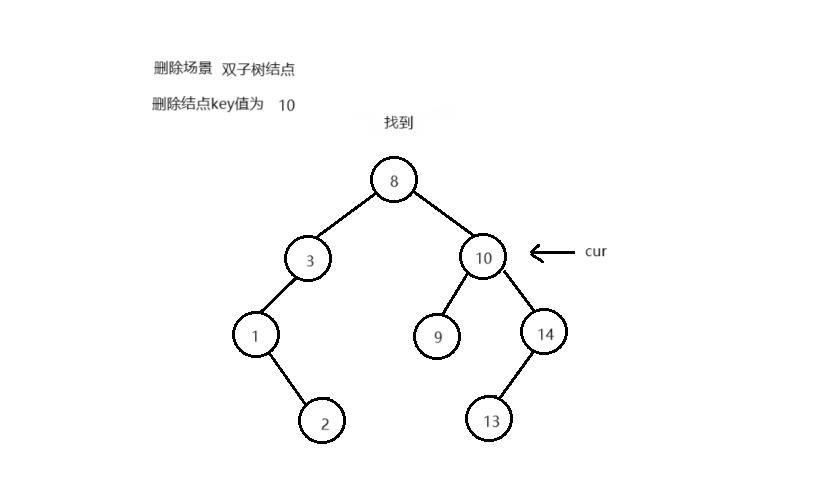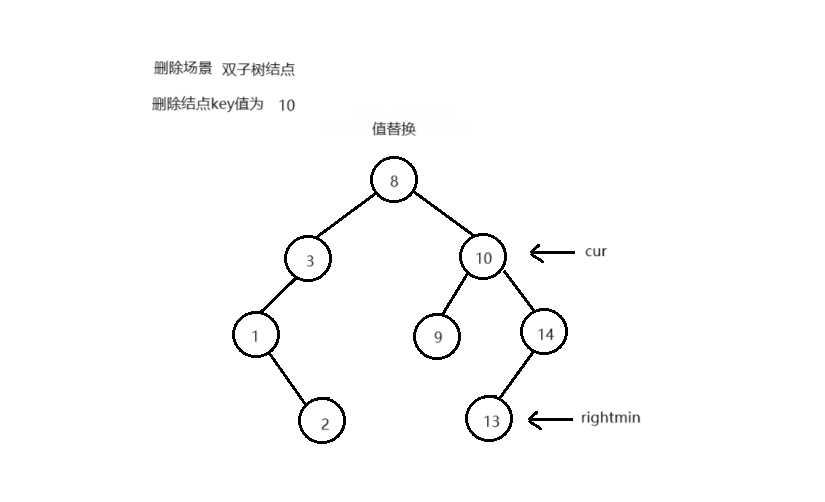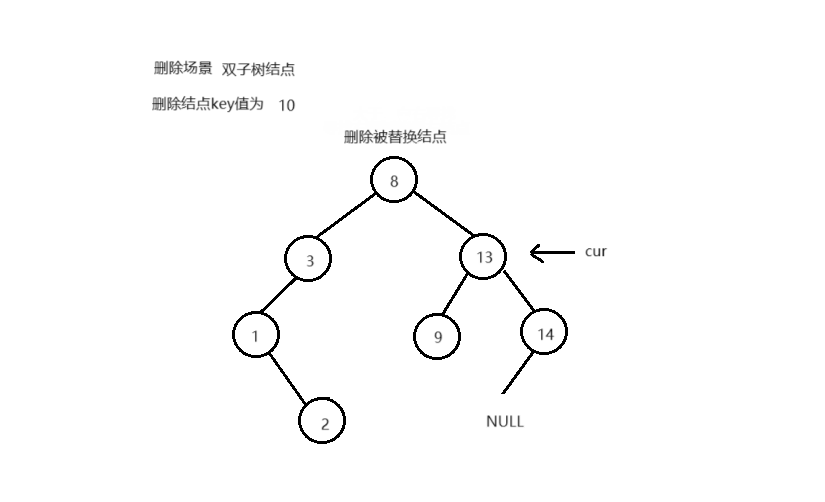
  1. 删除结点后，不能破坏搜索树的结构
  2. 删除不同类型结点的场景，删除逻辑：
    <1> 叶子结点，直接删除，父节点链接指针置空
    <2> 单子树结点，托孤，即，将自己的子树链接给父结点
    <3> 双子树结点，寻找key值最接近的结点（左子树的最右结点，右子树的最左结点），值替换被删除的结点，而后删除被替换的结点
  1. 叶子结点
    在这里插入图片描述
  2. 单子树结点
    在这里插入图片描述
  3. 双子树结点
    在这里插入图片描述
//非递归
bool Erase(T key)
{
	BSNode* cur = _root;
	BSNode* parent = nullptr;
	while (cur)
	{
		//查找到删除结点的位置
		if (key < cur->_key)
		{
			parent = cur;
			cur = cur->_left;
		}
		else if (key > cur->_key)
		{
			parent = cur;
			cur = cur->_right;
		}
		else//找到了
		{
			//叶子结点与单子树结点的删除
			//可以合并共用一套逻辑
			if (cur->_left == nullptr || cur->_right == nullptr)//叶子结点/单子树
			{
				//根结点特殊处理
				if (cur == _root)
				{
					if (cur->_left)
					{
						_root = cur->_left;
					}
					else
					{
						_root = cur->_right;
					}

					delete cur;
				}
				else//普通结点
				{
					//托孤
					if (cur->_left)//左单子树
					{
						if (cur == parent->_left)
						{
							parent->_left = cur->_left;
						}
						else
						{
							parent->_right = cur->_left;
						}
						delete cur;
					}
					else//右单子树/叶子节点
					{
						if (cur == parent->_left)
						{
							parent->_left = cur->_right;
						}
						else
						{
							parent->_right = cur->_right;
						}
						delete cur;
					}
				}

				return true;
			}
			else//双子树
			{
				//寻找右子树的最左结点
				BSNode* RightParent = cur;
				BSNode* RightMin = cur->_right;

				while (RightMin->_left)
				{
					RightParent = RightMin;
					RightMin = RightMin->_left;
				}

				//值替换
				cur->_key = RightMin->_key;

				//删除被替换结点
				//删除结点的左孩子一定为空，所以按照右子树结点处理
				//托孤
				if (RightMin == RightParent->_left)
				{
					RightParent->_left = RightMin->_right;
				}
				else
				{
					RightParent->_right = RightMin->_right;
				}

				//删除
				delete RightMin;

				return true;
			}
		}
	}

	//未找到
	return false;
}

//递归
bool _EraseR(BSNode*& cur, T key)
{
	if (cur == nullptr)
	{
		return false;
	}

	//寻找删除结点
	if (key < cur->_key)
	{
		return _EraseR(cur->_left, key);
	}
	else if (key > cur->_key)
	{
		return _EraseR(cur->_right, key);
	}
	else//找到了
	{
		//使用传引用后，对操作的优化
		if (cur->_left == nullptr || cur->_right == nullptr)//叶子结点/单子树结点
		{
			BSNode* del = cur;
			if (cur->_left)
			{
				cur = cur->_left;
			}
			else
			{
				cur = cur->_right;
			}
			delete del;

			return true;
		}
		else//双子树
		{
			//寻找右子树的最左结点
			BSNode* RightMin = cur->_right;
			while (RightMin->_left)
			{
				RightMin = RightMin->_left;
			}

			//值替换
			cur->_key = RightMin->_key;

			//值替换后，删除结点传值改变
			//转化为单子树删除，调用单子树删除处理
			_EraseR(cur->_right, cur->_key);
		}
	}

	assert(true);
	return false;
}

1.3.5 中序遍历

void _InOrder(BSNode* cur)
{
	if (cur == nullptr)
	{
		return;
	}

	//左根右
	_InOrder(cur->_left);
	cout << cur->_key << " ";
	_InOrder(cur->_right);
}

void InOrder()
{
	_InOrder(_root);
	cout << endl;
}

2. 二叉树进阶相关练习

2.1 根据二叉树创建字符串

  1. 题目信息：
    在这里插入图片描述
  2. 题目连接：
    根据二叉树创建字符串
class Solution 
{
public:
    void _tree2str(string& str, TreeNode* cur)
    {
        if(cur == nullptr)
        {
            return;
        }
        //字符串转字符串stoi（整形），stod（浮点型）
        str += to_string(cur->val);

        //除左空右不空的情况外，其余省略
        if(cur->left || cur->right)
        {
            str += "(";
            _tree2str(str, cur->left);
            str += ")";
        }

        if(cur->right)
        {
            str += "(";
            _tree2str(str, cur->right);
            str += ")";
        }
    }

    string tree2str(TreeNode* root) 
    {
        string ret;
        //递归
        _tree2str(ret, root);

        return ret;
    }
};

2.2 二叉树的层序遍历I

  1. 题目信息：
    在这里插入图片描述
  2. 题目连接：
    二叉树的层序遍历I
  3. 思路：levelsize计数
class Solution
{
public:
    vector<vector<int>> levelOrder(TreeNode* root)
    {
        //levelsize计数
        vector<vector<int>> ret;
        queue<TreeNode*> q;
        int levelsize = 1;
        q.push(root);
        //可能为空树
        if(root == nullptr)
        {
            return ret;
        }

        while (!q.empty())
        {
            vector<int> count;
            while (levelsize--)
            {
                //记录
                TreeNode* top = q.front();
                q.pop();
                count.push_back(top->val);
                //插入新结点
                if (top->left)
                    q.push(top->left);
                if (top->right)
                    q.push(top->right);
            }
            levelsize = q.size();
            ret.push_back(count);
        }

        return ret;
    }
};

2.3 二叉树层序遍历II

  1. 题目信息：
    在这里插入图片描述
  2. 题目连接：
    二叉树层序遍历II
  3. 思路：反转自上至下的层序遍历
class Solution 
{
public:
    vector<vector<int>> levelOrderBottom(TreeNode* root) 
    {
        //全部压栈，无法判断层
        //得出自上至下的序列，然后逆置
        vector<vector<int>> ret;
        if(root == nullptr)
        {
            return ret;
        }
        queue<TreeNode*> q;
        int levelsize = 1;
        q.push(root);
        while(!q.empty())
        {
            vector<int> count;
            while(levelsize--)
            {
                TreeNode* cur = q.front();
                q.pop();
                count.push_back(cur->val);
                if(cur->left)
                    q.push(cur->left);
                if(cur->right)
                    q.push(cur->right);
            }
            levelsize = q.size();
            ret.push_back(count);
        }

        reverse(ret.begin(), ret.end());

        return ret;
    }
};

2.4 二叉树最近公共祖先结点

  1. 题目信息：
    在这里插入图片描述
  2. 二叉树最近公共祖先结点
  3. 思路：
    <1> 方法1：p与q一定分别在祖先结点的左侧与右侧，祖先结点可能是自己
    <2> 方法2：栈记录遍历路径，路径上的所有祖先结点
//方法1：
class Solution 
{
public:
    bool SearchNode(TreeNode* cur, TreeNode* search)
    {
        if(cur == nullptr)
        {
            return false;
        }

        if(cur == search)
        {
            return true;
        }

        return SearchNode(cur->left, search) || SearchNode(cur->right, search);
    }

    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) 
    {
        bool qInleft = false;
        bool qInright = false;
        bool pInleft = false;
        bool pInright = false;
        TreeNode* cur = root;
        while(cur)
        {
            //可能最近祖先结点是自己
            if(cur == p)
            {
                pInleft = pInright = true;
            }
            else if(SearchNode(cur->left, p))
            {
                pInleft = true;
                pInright = false;
            }
            else
            {
                pInright = true;
                pInleft = false;
            }

            if(cur == q)
            {
                qInleft = qInright = true;
            }
            else if(SearchNode(cur->left, q))
            {
                qInleft = true;
                qInright = false;
            }
            else
            {
                qInright = true;
                qInleft = false;
            }

            if((pInleft && qInright) || (pInright && qInleft))
                break;
            else if(pInleft && qInleft)
                cur = cur->left;
            else
                cur = cur->right;
        }

        return cur;
    }
};

//方法2：
class Solution 
{
public:
    bool PreOrder(TreeNode* cur, TreeNode* search, stack<TreeNode*>& count)
    {
        if(cur == nullptr)
        {
            return false;
        }

        count.push(cur);

        if(cur == search)
        {
            return true;
        }

        if(!PreOrder(cur->left, search, count) && !PreOrder(cur->right, search, count))
        {
            count.pop();
        }
        else
        {
            return true;
        }

        assert(true);
        return false;
    }

    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) 
    {
        //栈记录遍历路径,所有祖先结点
        //到达指定结点的路径只有一条
        //深度优先遍历
        stack<TreeNode*> p_st;
        stack<TreeNode*> q_st;
        PreOrder(root, p, p_st);
        PreOrder(root, q, q_st);

        //路径上的相交结点
        while(p_st.size() != q_st.size())
        {
            if(p_st.size() > q_st.size())
                p_st.pop();
            else
                q_st.pop();
        }

        while(p_st.top() != q_st.top())
        {
            p_st.pop();
            q_st.pop();
        }

        return p_st.top();

    }
};

2.5 二叉树搜索与双向链表

  1. 题目信息：
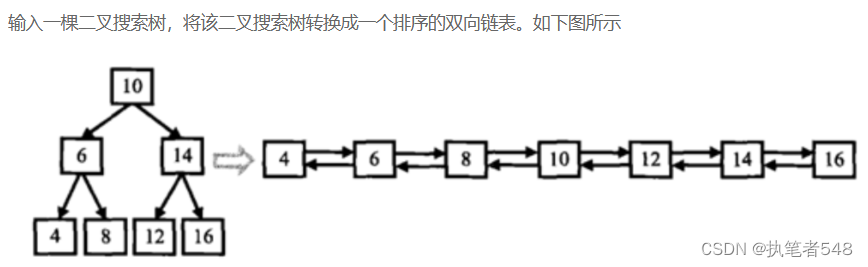
    在这里插入图片描述
  2. 题目链接：
    二叉搜索树与双向链表
  3. 思路：记录前置结点，中序遍历，注意调整指针链接的时机
class Solution 
{
public:
	void InOrder(TreeNode* cur, TreeNode*& pre)
	{
		if(cur == nullptr)
		{
			return;
		}

		InOrder(cur->left, pre);
		cur->left = pre;
		if(pre)
			pre->right = cur;
		
		pre = cur;
		InOrder(cur->right, pre);
	}

    TreeNode* Convert(TreeNode* pRootOfTree) 
	{
		if(pRootOfTree == nullptr)
		{
			return nullptr;
		}

		TreeNode* pre = nullptr;
		InOrder(pRootOfTree, pre);
		while(pRootOfTree->left)
		{
			pRootOfTree = pRootOfTree->left;
		}

		return pRootOfTree;
    }
};

2.6 从前序与中序遍历序列构造二叉树

  1. 题目信息：
    在这里插入图片描述
  2. 题目链接：
    从前序与中序遍历序列构造二叉树
  3. 思路：根据根分割出左右子树，区域分割，引用
class Solution 
{
public:
    TreeNode* buildNode(vector<int>& preorder, vector<int>& inorder, int& i, int left, int right)
    {
        if(left > right)
        {
            return nullptr;
        }

        //在中序中找到需构建结点
        int j = 0;
        while(inorder[j] != preorder[i])
        {
            j++;
        }

        //根左右
        //构建
        TreeNode* newnode = new TreeNode(preorder[i++]);
        //分割域，判断，构建左孩子
        newnode->left = buildNode(preorder, inorder, i, left, j - 1);
        //分割域，判断，构建右孩子
        newnode->right = buildNode(preorder, inorder, i, j + 1, right);
        
        return newnode;
    }

    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) 
    {
        int i = 0;
        return buildNode(preorder, inorder, i, 0, inorder.size() - 1);
    }
};

2.7 从中序与后序遍历序列构造二叉树

  1. 题目信息：
    在这里插入图片描述
  2. 题目链接：
    从中序与后序遍历序列构造二叉树
  3. 思路：区域分割判断，引用，逆向遍历，根右左
class Solution 
{
public:
    TreeNode* buildNode(vector<int>& inorder, vector<int>& postorder, int& i, int left, int right)
    {
        if(left > right)
        {
            return nullptr;
        }

        int j = 0;
        while(inorder[j] != postorder[i])
        {
            j++;
        }

        TreeNode* newnode = new TreeNode(postorder[i--]);
        newnode->right = buildNode(inorder, postorder, i, j + 1, right);
        newnode->left = buildNode(inorder, postorder, i, left, j - 1);

        return newnode;
    }

    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) 
    {
        //逆向遍历，根右左
        int i = postorder.size() - 1;
        return buildNode(inorder, postorder, i, 0, postorder.size() - 1);
    }
};

2.8 二叉树前序遍历（非递归）

  1. 题目信息：
    在这里插入图片描述
  2. 题目链接：
    二叉树前序遍历
  3. 思路：根左右，插入右子树时就将根删除，栈记录
class Solution 
{
public:
    vector<int> preorderTraversal(TreeNode* root) 
    {
        //非递归，前序遍历，根左右
        vector<int> ret;
        TreeNode* cur = root;
        stack<TreeNode*> st;
        while(cur || !st.empty())
        {
            while(cur)
            {
                st.push(cur);
                ret.push_back(cur->val);
                cur = cur->left;
            }

            TreeNode* top = st.top();
            st.pop();
            cur = top->right;
        }

        return ret;
    }
};

2.9 二叉树中序遍历（非递归）

  1. 题目信息：
    在这里插入图片描述
  2. 题目链接：
    二叉树中序遍历
  3. 思路：插入时机，删除时插入，左右根
class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) 
    {
        //中序，左右根
        vector<int> ret;
        stack<TreeNode*> st;
        TreeNode* cur = root;
        //插入时机，删除时插入
        while(cur || !st.empty())
        {
            while(cur)
            {
                st.push(cur);
                cur = cur->left;
            }

            TreeNode* top = st.top();
            st.pop();
            ret.push_back(top->val);

            cur = top->right;
        }

        return ret;
    }
};

!!!3.10 二叉树后序遍历（非递归）

  1. 题目信息：
    在这里插入图片描述
  2. 题目链接：
    二叉树后续遍历
  3. 思路：二次遍历时删除，删除时插入，何时删除
class Solution 
{
public:
    vector<int> postorderTraversal(TreeNode* root) 
    {
        //左右根
        vector<int> ret;
        stack<TreeNode*> st;
        TreeNode* cur = root;
        TreeNode* pre = nullptr;
        while(cur || !st.empty())
        {
            //左
            while(cur)
            {
                st.push(cur);
                cur = cur->left;
            }
            
            //根
            TreeNode* top = st.top();
            //cur = st.top();
            if(top->right == nullptr || pre == top->right)
            //if(cur->right == nullptr || pre == cur->right)
            {
                st.pop();
                pre = top;
                //pre = cur;
                ret.push_back(top->val);
                //ret.push_back(cur->val);
            }
            else
            {
                //右，死循环
                cur = top->right;
                //cur调整错误
                //cur = cur->right;
            }
        }

        return ret;
    }
};

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1611755.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

ChatGPT研究论文提示词集合1-【主题选择与问题研究、文献综述】

ChatGPT研究论文提示词集合1-【主题选择与问题研究、文献综述】

点击下方▼▼▼▼链接直达AIPaperPass &#xff01; AIPaperPass - AI论文写作指导平台 目录 1.主题选择与问题定义 2.文献综述 3.书籍介绍 AIPaperPass智能论文写作平台 近期小编按照学术论文的流程&#xff0c;精心准备一套学术研究各个流程的提示词集合。总共14个步骤…
阅读更多...
AI翻译英语PDF文档的3种方法

AI翻译英语PDF文档的3种方法

短的文章&#xff0c;直接丢进kimichat、ChatGPT里面很快就可以翻译完成&#xff0c;而且效果很佳。但是&#xff0c;很长的PDF文档整篇需要翻译&#xff0c;怎么办呢&#xff1f; ●腾讯交互翻译TranSmart https://transmart.qq.com/ 软件下载后&#xff0c;点击左边的文件翻…
阅读更多...
天才简史——Sylvain Calinon

天才简史——Sylvain Calinon

一、研究方向 learning from demonstration&#xff08;LfD&#xff09;领域的专家&#xff0c;机器人红宝书&#xff08;Springer handbook of robotics&#xff09;Robot programming by demonstration章节的合作者。主要研究兴趣包括&#xff1a; 机器人学习、最优控制、几…
阅读更多...
从零自制docker-11-【pivotRoot切换实现文件系统隔离】

从零自制docker-11-【pivotRoot切换实现文件系统隔离】

文章目录 busyboxdocker run -d busybox topcontainerId(docker ps --filter "ancestorbusybox:latest"|grep -v IMAGE|awk {print $1})docker export -o busybox.tar $containerId or sudo docker export 09bbf421d93f > ./busybox.tar tar -xvf busybox.tar -C …
阅读更多...
Python | Leetcode Python题解之第41题缺失的第一个正数

Python | Leetcode Python题解之第41题缺失的第一个正数

题目&#xff1a; 题解&#xff1a; class Solution:def firstMissingPositive(self, nums: List[int]) -> int:n len(nums)for i in range(n):while 1 < nums[i] < n and nums[nums[i] - 1] ! nums[i]:nums[nums[i] - 1], nums[i] nums[i], nums[nums[i] - 1]for …
阅读更多...
域名信息查询同款WHOIS源码

域名信息查询同款WHOIS源码

域名查询一般是指查询域名的whois注册信息&#xff0c;域名WHOIS是当前域名系统中不可或缺的一项信息服务。在使用域名进行Internet冲浪时&#xff0c;很多用户希望进一步了解域名、名字服务器详细信息&#xff0c;这就会用到WHOIS。 域名信息查询同款WHOIS源码
阅读更多...
在Postgres中，如何有效地管理大型数据库的大小和增长

在Postgres中，如何有效地管理大型数据库的大小和增长

文章目录 一、定期清理和维护1. VACUUM和ANALYZE2. 删除旧数据和归档 二、分区表三、压缩数据四、配置优化1. 调整维护工作负载2. 监控和日志 五、使用外部存储和扩展1. 外部表和FDW2. 扩展和插件 六、定期备份和恢复测试结论 管理大型数据库的大小和增长是数据库管理员&#x…
阅读更多...
EA包图上嵌套的包位置不对

EA包图上嵌套的包位置不对

Extreme 2024-4-11 11:36 我从工具栏把一个包拖在另一个包里面&#xff0c;可是项目树上两个包的位置并列&#xff0c;拖了几次结果都一样。我的目的是做一个多层级的包图&#xff0c;是不是&#xff08;EA&#xff09;不能在图上做&#xff1f; UMLChina潘加宇 确实是这样&a…
阅读更多...
m个人的成绩存放在score数组中，请编写函数fun，它的功能是：将低于平均分的人数作为函数值返回，将低于平均分的分数放在below所指的数组中。

m个人的成绩存放在score数组中，请编写函数fun，它的功能是：将低于平均分的人数作为函数值返回，将低于平均分的分数放在below所指的数组中。

本文收录于专栏：算法之翼 https://blog.csdn.net/weixin_52908342/category_10943144.html 订阅后本专栏全部文章可见。 本文含有题目的题干、解题思路、解题思路、解题代码、代码解析。本文分别包含C语言、C++、Java、Python四种语言的解法和详细的解析。 题干 m个人的成绩…
阅读更多...
强固型工业电脑在轮胎成型机设备行业应用

强固型工业电脑在轮胎成型机设备行业应用

轮胎成型机设备行业应用 项目背景 我国是一个轮胎生产与出口大国&#xff0c;在轮胎的生产过程中&#xff0c;成型工序是生产的关键工序&#xff0c;将半成品的部件按照轮胎的技术规范在成型机上组装成胎胚&#xff0c;工艺较为复杂&#xff0c;对设备加工和定位精度要求较高。…
阅读更多...
【Linux学习】gcc与g++的使用与程序翻译的过程

【Linux学习】gcc与g++的使用与程序翻译的过程

文章目录 修改sudo用户名单gcc与g指令gcc用法g用法 程序翻译的过程函数库动态库与静态库什么是动静态库&#xff1f;动静态库的优缺点ldd指令 这里补充一个前面遗漏的知识&#xff1a; 修改sudo用户名单 必须使用root超级用户进行修改&#xff0c;普通用户是不能访问修改。 …
阅读更多...
Spring 事务实现方式：

Spring 事务实现方式：

Spring 事务实现方式&#xff1a; Spring并不直接支持事务&#xff0c;只有当数据库支持事务的时候&#xff0c;Spring才支持事务&#xff0c;Spring只不过简化了开发人员实现事务的开发步骤 Spring事务的实现方式有两种&#xff1a; 一、基于申明式事务&#xff1a; Service…
阅读更多...
CCF-CSP真题《202312-2 因子化简》思路+python，c++满分题解

CCF-CSP真题《202312-2 因子化简》思路+python，c++满分题解

想查看其他题的真题及题解的同学可以前往查看&#xff1a;CCF-CSP真题附题解大全 试题编号&#xff1a;202312-2试题名称&#xff1a;因子化简时间限制&#xff1a;2.0s内存限制&#xff1a;512.0MB问题描述&#xff1a; 题目背景 质数&#xff08;又称“素数”&#xff09;是指…
阅读更多...
安装AngusTester节点代理

安装AngusTester节点代理

一、介绍 节点代理程序(AngusAgent)提供三方面作用&#xff1a; 通过启动"执行器(AngusRunner)"来执行脚本任务。在代理节点上运行和管理Mock服务。收集、监控和报告关于节点的各种指标和性能数据&#xff0c;该数据用于在稳定性测试中可分析节点资源使用率。 二、…
阅读更多...
Java高阶私房菜：高并发之线程池底层原理学习

Java高阶私房菜：高并发之线程池底层原理学习

以往我们需要获取外部资源&#xff08;数据源、Http请求等&#xff09;时&#xff0c;需要对目标源创建链接对象&#xff0c;三次握手成功后方可正常使用&#xff0c;为避免持续的资源占用和可能的内存泄漏&#xff0c;还需要调用目标对象close方法释放资源销毁对象。这一建一销…
阅读更多...
【PCL】教程conditional_euclidean_clustering 对输入的点云数据进行条件欧式聚类分析...

【PCL】教程conditional_euclidean_clustering 对输入的点云数据进行条件欧式聚类分析...

[done, 3349.09 ms : 19553780 points] Available dimensions: x y z intensity 源点云 Statues_4.pcd 不同条件函数output.pcd 【按5切换到强度通道可视化】 终端输出&#xff1a; Loading... >> Done: 1200.46 ms, 19553780 points Downsampling... >> Done: 411…
阅读更多...
ssm064农产品仓库管理系统系统+jsp

ssm064农产品仓库管理系统系统+jsp

农产品仓库管理系统设计与实现 摘 要 现代经济快节奏发展以及不断完善升级的信息化技术&#xff0c;让传统数据信息的管理升级为软件存储&#xff0c;归纳&#xff0c;集中处理数据信息的管理方式。本农产品仓库管理系统就是在这样的大环境下诞生&#xff0c;其可以帮助管理者…
阅读更多...
Llama 3“智商”测试：英文提示表现亮眼，中文不完美但差强人意！

Llama 3“智商”测试：英文提示表现亮眼，中文不完美但差强人意！

大家好&#xff0c;我是木易&#xff0c;一个持续关注AI领域的互联网技术产品经理&#xff0c;国内Top2本科&#xff0c;美国Top10 CS研究生&#xff0c;MBA。我坚信AI是普通人变强的“外挂”&#xff0c;所以创建了“AI信息Gap”这个公众号&#xff0c;专注于分享AI全维度知识…
阅读更多...
C++从入门到精通——C++动态内存管理

C++从入门到精通——C++动态内存管理

C动态内存管理 前言一、C/C内存分布分类1分类2题目选择题sizeof 和 strlen 区别示例sizeofstrlen 二、C语言中动态内存管理方式malloc/calloc/realloc/free示例例题malloc/calloc/realloc的区别malloc的实现原理 三、C内存管理方式new/delete操作内置类型new和delete操作自定义…
阅读更多...
zabbix自定义监控、自动发现和注册以及代理设置

zabbix自定义监控、自动发现和注册以及代理设置

前言 监控项的定制和新设备的注册往往需要大量手动操作&#xff0c;这会导致维护成本的增加和监控效率的降低。本文将介绍如何利用 Zabbix 的自定义功能&#xff0c;实现监控项的动态发布和新设备的自动注册以及代理设置、从而简化运维工作并实现更高效的监控管理。 Zabbix 监…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023