专题【二分查找】刷题日记

news2024/10/6 12:30:46

题目列表

4. 寻找两个正序数组的中位数
33. 搜索旋转排序数组
34. 在排序数组中查找元素的第一个和最后一个位置
35. 搜索插入位置
69. x 的平方根
167. 两数之和 II - 输入有序数组
209. 长度最小的子数组
222. 完全二叉树的节点个数
287. 寻找重复数

2023.04.14

4. 寻找两个正序数组的中位数

题目

给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。

算法的时间复杂度应该为 O(log (m+n)) 。

示例 1：

输入：nums1 = [1,3], nums2 = [2]
输出：2.00000
解释：合并数组 = [1,2,3] ，中位数 2

示例 2：

输入：nums1 = [1,2], nums2 = [3,4]
输出：2.50000
解释：合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5

提示：

  • nums1.length == m
  • nums2.length == n
  • 0 <= m <= 1000
  • 0 <= n <= 1000
  • 1 <= m + n <= 2000
  • -106 <= nums1[i], nums2[i] <= 106

思路

  1. 总元素个数如果是奇数
  2. 每一个数组都找中间的指针
  3. 如果对于这俩指针， 左右恰巧数量一样，就返回这俩指针对应的元素（奇数返回小的，偶数返回两个的平均）
  4. a[0], …, a[i],…a[m-1]，b[0],…,b[j],…b[n-1]，左右一样指a[0]…a[i]元素个数加上b[0]…b[j]元素个数和剩余部分一致，并且a[i-1]<b[j]<a[i+1] && b[j-1] < a[i] < b[j+1]，即a[i]的坐边小于b[j]、b[j]的左边小于a[i]、a[i]的右边大于b[j]、b[j]的右边大于a[i]
  5. 否则使用二分查找其中一个，同时调整另一个元素的个数，始终保持，左右元素相等，直到满足上述第二个条件

答案

class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int m = nums1.length;
        int n = nums2.length;

        if (m > n) {
        	// 从短的做遍历。为了避免处理nums2的边界
            return findMedianSortedArrays(nums2, nums1);
        }
        int halfNum = (m + n + 1) / 2;

        int left = 0, right = m;
        int leftMax = 0, rightMin = 0;

        while (left <= right) {
        	// 防溢出
            int middle1 = left + (right - left) / 2;
            int middle2 = halfNum - middle1;
			
			// i_1要处理左溢出即==0的判断，i本身要处理右溢出即==m
			// MAX_VALUE还是MIN_VALUE是从max还是min赋值的，反正就是取合法的那边
            int ai_1 = middle1 == 0 ? Integer.MIN_VALUE : nums1[middle1 - 1];
            int ai = middle1 == m ? Integer.MAX_VALUE : nums1[middle1];
	
            int bj_1 = middle2 == 0 ? Integer.MIN_VALUE : nums2[middle2 - 1];
            int bj = middle2 == n ? Integer.MAX_VALUE : nums2[middle2];

			// 满足条件就记录
            if (ai_1 <= bj) {
                leftMax = Math.max(ai_1, bj_1);
                rightMin = Math.min(ai, bj);
                left = middle1 + 1;
            } else {
                right = middle1 - 1;
            }

        }
        // 满足条件才更新，所以直接返回
        return ((m + n) % 2 == 0) ? (leftMax + rightMin) / 2.0 : leftMax;

    }
}

33. 搜索旋转排序数组

题目

整数数组 nums 按升序排列，数组中的值 互不相同 。

在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了 旋转，使数组变为 [nums[k], nums[k+1], …, nums[n-1], nums[0], nums[1], …, nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。

给你 旋转后 的数组 nums 和一个整数 target ，如果 nums 中存在这个目标值 target ，则返回它的下标，否则返回 -1 。

你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

示例 1：

输入：nums = [4,5,6,7,0,1,2], target = 0
输出：4

示例 2：

输入：nums = [4,5,6,7,0,1,2], target = 3
输出：-1

示例 3：

输入：nums = [1], target = 0
输出：-1

提示：

  • 1 <= nums.length <= 5000
  • -104 <= nums[i] <= 104
  • nums 中的每个值都 独一无二
  • 题目数据保证 nums 在预先未知的某个下标上进行了旋转
  • -104 <= target <= 104

思路

核心是找到在哪边搜索

  1. 先判断哪边是有序的
  2. 如果目标值在有序的这边，就在这边，否则在另一边

答案

class Solution {
    public int search(int[] nums, int target) {
        return search(nums, target, 0, nums.length - 1);
    }

    public int search(int[] nums, int target, int left, int right) {
    	// 递归的边界
        if (left > right) {
            return -1;
        }

        int middle = left + (right - left) / 2;
        int value = nums[middle];
        // 递归的终止条件
        if (value == target) {
            return middle;
        } 
        // 左边有序
        if (nums[left] <= value) {
        	// 因为左边有序，所以判断在不在左边范围内，在的话就在左边
            if (target < value && nums[left] <= target) {
                return search(nums, target, left, middle - 1);
            } else {
                return search(nums, target, middle + 1, right);
            }
        } else {
        	// 右边同理
            if (target > value && target <= nums[right]) {
                return search(nums, target, middle + 1, right);
            } else {
                return search(nums, target, left, middle - 1);
            }
        }
    }
}

34. 在排序数组中查找元素的第一个和最后一个位置

题目

给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。

示例 1：

输入：nums = [5,7,7,8,8,10], target = 8
输出：[3,4]

示例 2：

输入：nums = [5,7,7,8,8,10], target = 6
输出：[-1,-1]

示例 3：

输入：nums = [], target = 0
输出：[-1,-1]

提示：

  • 0 <= nums.length <= 105
  • -109 <= nums[i] <= 109
  • nums 是一个非递减数组
  • -109 <= target <= 109

思路

和普通二分的区别是搜索到之后的动作

  1. 搜索最左边的话，就一直把右边界往左边移动。
  2. 右边同理，详见注释

答案

class Solution {
    public int[] searchRange(int[] nums, int target) {
        if (nums.length == 0) {
            return new int[] { -1, -1 };
        }
        return new int[] { lBsearch(nums, target, 0, nums.length - 1), rBsearch(nums, target, 0, nums.length - 1) };
    }

    public int lBsearch(int[] nums, int target, int left, int right) {
		// 因为左右都是闭区间，所以相等
        while (left <= right) {
            int middle = left + (right - left) / 2;
            int value = nums[middle];
            if (value < target) {
                left = middle + 1;
            } else {
            	// 相等就移动右边界
                right = middle - 1;
            }
        }
        // 考虑剩两个元素的时候，[m, target]，这时候middle==left, m < target，最后右移一步。所以最后，如果有left一定指向元素
        // 考虑剩两个元素的时候，[target, target]，这时候middle==left, 最后左移一步。所以最后，如果有left一定指向元素
        // 一些边界判断
        return left >= 0 && left < nums.length && nums[left] == target ? left : -1;
    }

	// 同搜索左边界
    public int rBsearch(int[] nums, int target, int left, int right) {
        while (left <= right) {
            int middle = left + (right - left) / 2;
            int value = nums[middle];
            if (value <= target) {
                left = middle + 1;
            } else {
                right = middle - 1;
            }
        }
        return right >= 0 && right < nums.length && nums[right] == target ? right : -1;
    }
}

2024.04.19

35. 搜索插入位置

题目

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

请必须使用时间复杂度为 O(log n) 的算法。

示例 1:

输入: nums = [1,3,5,6], target = 5
输出: 2

示例 2:

输入: nums = [1,3,5,6], target = 2
输出: 1

示例 3:

输入: nums = [1,3,5,6], target = 7
输出: 4

提示:

  • 1 <= nums.length <= 104
  • -104 <= nums[i] <= 104
  • nums 为 无重复元素 的 升序 排列数组
  • -104 <= target <= 104

思路

比二分查找，要多考虑下，最后left和right的位置关系
考虑两个元素的时候[m, n], m < target < n, nums[middle] = m < target，移动right，left和right重合在m，最后一次，right-1，left不动

答案

class Solution {
    public int searchInsert(int[] nums, int target) {
        int left = 0, right = nums.length - 1;
        // 闭区间，所以=
        while (left <= right) {
            int middle = left + (right - left) / 2;
            int value = nums[middle];

            if (value == target) {
                return middle;
            } else if (value < target) {
                left = middle + 1;
            } else {
                right = middle - 1;
            }
        }
        return left;
    }
}

69. x 的平方根

题目

给你一个非负整数 x ，计算并返回 x 的 算术平方根 。
由于返回类型是整数，结果只保留 整数部分 ，小数部分将被 舍去 。
注意：不允许使用任何内置指数函数和算符，例如 pow(x, 0.5) 或者 x ** 0.5 。

示例 1：

输入：x = 4
输出：2

示例 2：

输入：x = 8
输出：2
解释：8 的算术平方根是 2.82842…, 由于返回类型是整数，小数部分将被舍去。

提示：

  • 0 <= x <= 2^31 - 1

思路

0-x一半一半逼近，因为1 = 1 x 1, 所以x是闭区间

答案

class Solution {
    public int mySqrt(int x) {
    	// 边界0,1
        if (x < 2) {
            return x;
        }
        int left = 0, right = x;

        while (left <= right) {
            int middle = left + (right - left) / 2;
            if (x / middle == middle) {
                return middle;
            } else if (x / middle < middle) {
                right = middle - 1;
            } else {
                left = middle + 1;
            }
        }
        // 2.8取2，所以-1
        return left - 1;
    }
}

167. 两数之和 II - 输入有序数组

题目

给你一个下标从 1 开始的整数数组 numbers ，该数组已按 非递减顺序排列 ，请你从数组中找出满足相加之和等于目标数 target 的两个数。如果设这两个数分别是 numbers[index1] 和 numbers[index2] ，则 1 <= index1 < index2 <= numbers.length 。

以长度为 2 的整数数组 [index1, index2] 的形式返回这两个整数的下标 index1 和 index2。

你可以假设每个输入 只对应唯一的答案 ，而且你 不可以 重复使用相同的元素。

你所设计的解决方案必须只使用常量级的额外空间。

示例 1：

输入：numbers = [2,7,11,15], target = 9
输出：[1,2]
解释：2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。

示例 2：

输入：numbers = [2,3,4], target = 6
输出：[1,3]
解释：2 与 4 之和等于目标数 6 。因此 index1 = 1, index2 = 3 。返回 [1, 3] 。

示例 3：

输入：numbers = [-1,0], target = -1
输出：[1,2]
解释：-1 与 0 之和等于目标数 -1 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。

提示：

  • 2 <= numbers.length <= 3 * 104
  • -1000 <= numbers[i] <= 1000
  • numbers 按 非递减顺序 排列
  • -1000 <= target <= 1000
  • 仅存在一个有效答案

思路

因为有序，固定一个，另一个用二分

答案

// 二分，O（n log(n)）
class Solution {
    public int[] twoSum(int[] numbers, int target) {
        for (int i = 0; i < numbers.length; i++) {
            int current = numbers[i];
            int left = i + 1;
            int right = numbers.length - 1;
            while (left <= right) {
                int middle = left + (right - left) / 2;
                if (current + numbers[middle] == target) {
                    return new int[] { i + 1, middle + 1 };
                } else if (current + numbers[middle] < target) {
                    left = middle + 1;
                } else {
                    right = middle - 1;
                }
            }
        }
        return new int[] { -1, -1 };
    }
}
// 双指针 O(n)
class Solution {
    public int[] twoSum(int[] numbers, int target) {
        int left = 0, right = numbers.length - 1;
        while (left < right) {
            int leftValue = numbers[left];
            int rightValue = numbers[right];
            if (leftValue + rightValue == target) {
                return new int[] { left + 1, right + 1 };
            } else if (leftValue + rightValue < target) {
                left++;
            } else {
                right--;
            }
        }
        return new int[] { -1, -1 };
    }
}

209. 长度最小的子数组

题目

给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其总和大于等于 target 的长度最小的 连续
子数组 [numsl, numsl+1, …, numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

示例 1：

输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。

示例 2：

输入：target = 4, nums = [1,4,4]
输出：1

示例 3：

输入：target = 11, nums = [1,1,1,1,1,1,1,1]
输出：0

提示：

  • 1 <= target <= 109
  • 1 <= nums.length <= 105
  • 1 <= nums[i] <= 105

进阶：

  • 如果你已经实现 O(n) 时间复杂度的解法, 请尝试设计一个 O(n log(n)) 时间复杂度的解法。

思路

  1. 滑动窗口
  2. 前缀和+二分搜索。二分一定要有序，前缀和可以做到

答案

// 滑动窗口
class Solution {
    public int minSubArrayLen(int target, int[] nums) {
        int result = Integer.MAX_VALUE;
        int left = 0, right = 0;
        int sum = 0;
        while (right < nums.length) {
            sum += nums[right];

            while (sum >= target && left <= right) {
                result = Math.min(result, right - left + 1);
                sum -= nums[left++];
            }
            right++;

        }
        return result == Integer.MAX_VALUE ? 0 : result;
    }
}
// 前缀和+二分
class Solution {
    public int minSubArrayLen(int target, int[] nums) {
        int[] sums = new int[nums.length + 1];
        int sum = 0;
        for (int i = 1; i < sums.length; i++) {
            sum += nums[i - 1];
            sums[i] = sum;
        }

        int result = Integer.MAX_VALUE;
        for (int i = 0; i < sums.length; i++) {
            int current = sums[i];
            int left = i + 1, right = sums.length - 1;
            while (left <= right) {
                int middle = left + (right - left) / 2;
                int value = sums[middle];
                if (value - current >= target) {
                    result = Math.min(result, middle - i);
                    right = middle - 1;
                } else {
                    left = middle + 1;
                }
            }
        }
        return result == Integer.MAX_VALUE ? 0 : result;
    }
}

222. 完全二叉树的节点个数

题目

给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。

完全二叉树 的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。

示例 1：
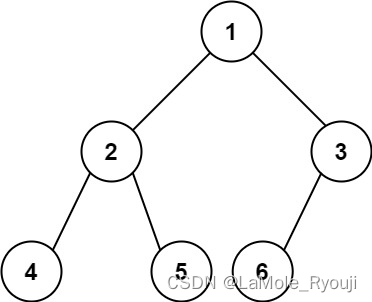
在这里插入图片描述

输入：root = [1,2,3,4,5,6]
输出：6

示例 2：

输入：root = []
输出：0

示例 3：

输入：root = [1]
输出：1

提示：

  • 树中节点的数目范围是[0, 5 * 104]
  • 0 <= Node.val <= 5 * 104
  • 题目数据保证输入的树是 完全二叉树

进阶： 遍历树来统计节点是一种时间复杂度为 O(n) 的简单解决方案。你可以设计一个更快的算法吗？

思路

  1. 因为是完全二叉树
  2. 求左右树的高度，如果相等，则说明左子树是完全二叉树，左子树元素个数是2左子树的高度-1，再加上根节点，就是2左子树的高度
  3. 如果不相等，说明右子树是完全二叉树，算法同2

答案

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int countNodes(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int left = high(root.left);
        int right = high(root.right);

        if (left == right) {
        	// 左子树是完全二叉树，左子树加右边的数量
            return countNodes(root.right) + (1 << left);
        } else {
        	// 右子树是完全二叉树，右子树加左边的数量
            return countNodes(root.left) + (1 << right);
        }
    }

    public int high(TreeNode root) {
        int result = 0;
        while (root != null) {
            result++;
            root = root.left;
        }
        return result;
    }
}

287. 寻找重复数

题目

给定一个包含 n + 1 个整数的数组 nums ，其数字都在 [1, n] 范围内（包括 1 和 n），可知至少存在一个重复的整数。
假设 nums 只有 一个重复的整数 ，返回 这个重复的数 。
你设计的解决方案必须 不修改 数组 nums 且只用常量级 O(1) 的额外空间。

示例 1：

输入：nums = [1,3,4,2,2]
输出：2

示例 2：

输入：nums = [3,1,3,4,2]
输出：3

示例 3 :

输入：nums = [3,3,3,3,3]
输出：3

提示：

  • 1 <= n <= 105
  • nums.length == n + 1
  • 1 <= nums[i] <= n
  • nums 中 只有一个整数 出现 两次或多次 ，其余整数均只出现 一次

进阶：

  • 如何证明 nums 中至少存在一个重复的数字?
  • 你可以设计一个线性级时间复杂度 O(n) 的解决方案吗？

思路

之前双指针有过，这次换个思路
要二分，必须有单调数组，有点像定义DP数组了、本次定义cnt[i]表示小于等于i的元素数量，有点像前缀和的逻辑，记住吧。数组构造单调数组有两个办法：前缀和、cnt[i]
如果数组中只有一个重复元素，根据题意 nums.length == n + 1 、1 <= nums[i] <= n，其实必然重复（n+1个位置，只有n个元素）。则重复元素之前，cnt[i] == i，[1,2,3,4,5,6,5,7,8]，这种cnt[0-4] = [0-4]，因为可能重复多个，所以cnt[i] <= i
用二分找到这个就行了，就是哪个位置开始出现不小于等于

答案

class Solution {
    public int findDuplicate(int[] nums) {
        int left = 0, right = nums.length - 1;
        int result = 0;
        // 找数，数在0-n之间（根据题意nums.length==n+1），搜索的是小于等于xxx
        while (left <= right) {
        	// 二分找数
            int middle = left + (right - left) / 2;
            // 计算cnt
            int cnt = 0;
            for (int i = 0; i < nums.length; i++) {
            	// 遍历数组，小于等于middle的数个数
                if (nums[i] <= middle) {
                    cnt++;
                }
            }
            // 是不是满足条件，满足说明数小了
            if (cnt <= middle) {
                left = middle + 1;
            } else {
            	// 记录下，因为可能是大于target的，所以继续搜索
            	// [1,2,3,4,5,6,5,7,8]，cnt[6] = 7, cnt[5] = 6, cnt[8] = 8，都满足条件，所以继续搜索
                result = middle;
                right = middle - 1;
            }
        }
        return result;
    }
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1611293.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

STM32G431RBT6之时钟树配置与生成工程

STM32G431RBT6之时钟树配置与生成工程

默认大家都下载了蓝桥杯嵌入式资源包了哈. 首先,打开cubumx,修改RCC与SYS. 打开并观察原理图,发现晶振是24Mhz. 第一步,打开Clock Configuration. 第二步,修改晶振为原理图相对应的24Mhz. 第三步,切换到HSE. 第四步,切换到PLLCLK. 第五步,设置HCLK为80Mhz(15届真题要求为8…
阅读更多...
【银角大王——Django课程——ORM】

【银角大王——Django课程——ORM】

Django课程——ORM框架 Django 模型使用自带的 ORMORM 解析过程:ORM 对应关系表&#xff1a;下载mysqlclient安装包创建数据库——ORM只能操作表&#xff0c;无法创建数据库。连接数据库——修改settings中的DATABASESDjango操作表&#xff0c;在models.py文件中编写——操作表…
阅读更多...
数字接龙（蓝桥杯）

数字接龙（蓝桥杯）

文章目录 数字接龙【问题描述】解题思路DFS 数字接龙 【问题描述】 小蓝最近迷上了一款名为《数字接龙》的迷宫游戏&#xff0c;游戏在一个大小为N N 的格子棋盘上展开&#xff0c;其中每一个格子处都有着一个 0 . . . K − 1 之间的整数。游戏规则如下&#xff1a; 从左上…
阅读更多...
专利基础概念

专利基础概念

专利是一种知识产权形式&#xff0c;它为发明创造提供了一种法律保护机制&#xff0c;允许发明者在一定期限内对其发明享有独占权。 1、专利类型 专利类型&#xff0c;也被称为专利的客体&#xff0c;是指符合专利授予条件的各种发明创造。根据中国专利法&#xff0c;发明创造…
阅读更多...
【经典小游戏】猜数字

【经典小游戏】猜数字

前言1. 游戏介绍2. 游戏实现3. 游戏优化结语 个人主页&#xff1a;C_GUIQU 前言 各位小伙伴大家好&#xff01; 先问大家一个问题&#xff1a;我们为什么要学习&#xff1f; 简单来说&#xff0c;就是为了实践&#xff01;只有不断学习才可以帮助我们更好地实践&#xff01; 小…
阅读更多...
【Java网络编程】网络编程中的基本概念及实现UDP、TCP客户端服务器程序

【Java网络编程】网络编程中的基本概念及实现UDP、TCP客户端服务器程序

目录 一、什么是网络编程&#xff1f; 二、网络编程中的基本概念 1. 客户端和服务器 2. 请求和响应 三、Socket套接字 UDP数据报套接字编程 1. DatagramSocket 2. DatagramPacket 3. UDP回显客户端服务器程序 4. UDP字典客户端服务器程序 TCP流套接字编程 1. Serve…
阅读更多...
【JS】js数字转k、w结尾 | 1000 = 1k

【JS】js数字转k、w结尾 | 1000 = 1k

问题 数字转k、w结尾 如&#xff1a;10001k 100001w 码 /*** 数字转k,w* param {Number} num * returns String*/ const numberTokw num > {if (num < 1000) return numlet endStr w,numVal 10000;if (num > 999 && num < 10000) {endStr knumVal …
阅读更多...
设计模式之创建型模式详解

设计模式之创建型模式详解

设计模式 创建型模式 创建型模式(Creational Pattern)对类的实例化过程进行了抽象&#xff0c;能够将软件模块中对象的创建和对象的使用分离。为了使软件的结构更加清晰&#xff0c;外界对于这些对象只需要知道它们共同的接口&#xff0c;而不清楚其具体的实现细节&#xff0…
阅读更多...
物联网实战--驱动篇之(九)NB-IOT(BC260)

物联网实战--驱动篇之(九)NB-IOT(BC260)

目录 一、NB-IOT简介 二、NB-IOT要素 三、代码详解 四、平台端 一、NB-IOT简介 实际上&#xff0c;就是NB-Iot彻底引爆了物联网的&#xff0c;大概2018年左右&#xff0c;NB推广如火如荼&#xff0c;同时广域网、低功耗的LPWAN网络也逐渐传开&#xff0c;现在回头来看&…
阅读更多...
Flyweight 享元

Flyweight 享元

意图 运用共享技术有效地支持大量细粒度的对象。 结构 其中 Flyweight描述一个接口&#xff0c;通过这个接口Flyweight可以接受并作用于外部状态。ConcreteFlyweight实现Flyweight接口&#xff0c;并作为内部状态&#xff08;如果有&#xff09;增加存储空间。ConcreteFlywe…
阅读更多...
[Java基础揉碎]集合

[Java基础揉碎]集合

目录 集合的理解和好处 数组 集合的理解和好处 继承图 ​编辑 简单实例 Collection接口和常用方法 1) add:添加单个元素 2) remove:删除指定元素 3) contains:查找元素是否存在 4) size:获取元素个数 5) isEmpty:判断是否为空 ​编辑 6) clear:清空 7) addAll:添…
阅读更多...
Prior Knowledge-Guided Transformer for Remote Sensing Image Captioning

Prior Knowledge-Guided Transformer for Remote Sensing Image Captioning

Prior Knowledge-Guided Transformer for Remote Sensing Image Captioning 1. 摘要 遥感图像(RSI)字幕生成旨在为遥感图像生成有意义且语法正确的句子描述。然而,相比于自然图像字幕,RSI字幕生成面临着由于RSI特性而产生的额外挑战。第一个挑战源于这些图像中存在大量物体。…
阅读更多...
ssh-key关于authorized_keys电脑与linux互相认证

ssh-key关于authorized_keys电脑与linux互相认证

思路&#xff1a; 在A上生成公钥私钥。将公钥拷贝给server B&#xff0c;要重命名成authorized_keys(从英文名就知道含义了)Server A向Server B发送一个连接请求。Server B得到Server A的信息后&#xff0c;在authorized_key中查找&#xff0c;如果有相应的用户名和IP&#xf…
阅读更多...
冰达ROS机器人快速使用指南

冰达ROS机器人快速使用指南

欢迎来到《冰达ROS机器人极简使用指南》 Q&#xff1a;这份教程适合谁&#xff1f; A&#xff1a;适合完全0基础新手&#xff0c;需要快速跑起来机器人的基本功能。也适合技术大佬需要快速的了解冰达ROS机器人的使用方法。 Q&#xff1a;这份教程内容很少&#xff0c;是不是…
阅读更多...
路由器热备份

路由器热备份

HSRP HSRP&#xff08;Hot Standby Routing Protocol&#xff09;热备份路由选择协议 HSRP是思科私有的协议&#xff0c;HSRP起到一个双网关热备份的一个目的&#xff0c;不考虑线路问题针对设备而言&#xff0c;一个设备挂了还有另外一台设备&#xff0c;所以双网关也叫双机…
阅读更多...
动力学重构/微分方程参数拟合 - 基于模型

动力学重构/微分方程参数拟合 - 基于模型

这一篇文章&#xff0c;主要是给非线性动力学&#xff0c;对微分方程模型参数拟合感兴趣的朋友写的。笼统的来说&#xff0c;这与混沌系统的预测有关&#xff1b;传统的机器学习的模式识别虽然也会谈论预测结果&#xff0c;但他们一般不会涉及连续的预测。这里我们考虑的是&…
阅读更多...
URL地址解析至页面展示全过程（面试详细解答）

URL地址解析至页面展示全过程（面试详细解答）

目录 1、解析URL 2、缓存判断 ​编辑3、DNS解析 ​编辑4、获取MAC地址 5、TCP三次握手 6、HTTP请求 7、服务器处理请求&#xff0c;返回HTTP响应 8、页面渲染 9、TCP四次挥手 10、浏览器解析HTML 11、浏览器布局渲染 1、解析URL 首先会对 URL 进行解析&#xff0c;…
阅读更多...
C++_类型转换

C++_类型转换

文章目录 学习目标&#xff1a;1.static_cast2. reinterpret_cast3.const_cast4. dynamic_cast 学习过程1.static_cast2. reinterpret_cast3.const_cast在这里插入图片描述4. dynamic_cast 学习目标&#xff1a; 标准C为了加强类型转换的可视性&#xff0c;引入了四种命名的强…
阅读更多...
黑马程序员Linux简单入门学习笔记

黑马程序员Linux简单入门学习笔记

Linux介绍 内核提供系统最核心的功能&#xff0c;如: 调度CPU、调度内存、调度文件系统、调度网络通讯、调度等系统级应用程序&#xff0c;可以理解为出厂自带程序&#xff0c;可供用户快速上手操作系统&#xff0c;如:文件管理器、任务管理器、图片查看、音乐播放等 目录结构 …
阅读更多...
在PostgreSQL中如何实现递归查询，例如使用WITH RECURSIVE构建层次结构数据？

在PostgreSQL中如何实现递归查询，例如使用WITH RECURSIVE构建层次结构数据？

文章目录 解决方案使用WITH RECURSIVE进行递归查询示例代码 总结 在PostgreSQL中&#xff0c;递归查询是一种非常强大的工具&#xff0c;它可以用来查询具有层次结构或树形结构的数据。例如&#xff0c;你可能会在员工-经理关系、目录结构或组织结构图中遇到这样的数据。为了处…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023