题目列表

3110. 字符串的分数

3111. 覆盖所有点的最少矩形数目

3112. 访问消失节点的最少时间

3113. 边界元素是最大值的子数组数目

一、字符串的分数

按照题目要求，直接模拟遍历即可，代码如下

class Solution {
public:
    int scoreOfString(string s) {
        int ans = 0;
        int n = s.size();
        for(int i=1;i<n;i++){
            ans += abs(s[i]-s[i-1]);
        }
        return ans;
    }
};

二、覆盖所有点的最小矩阵数目

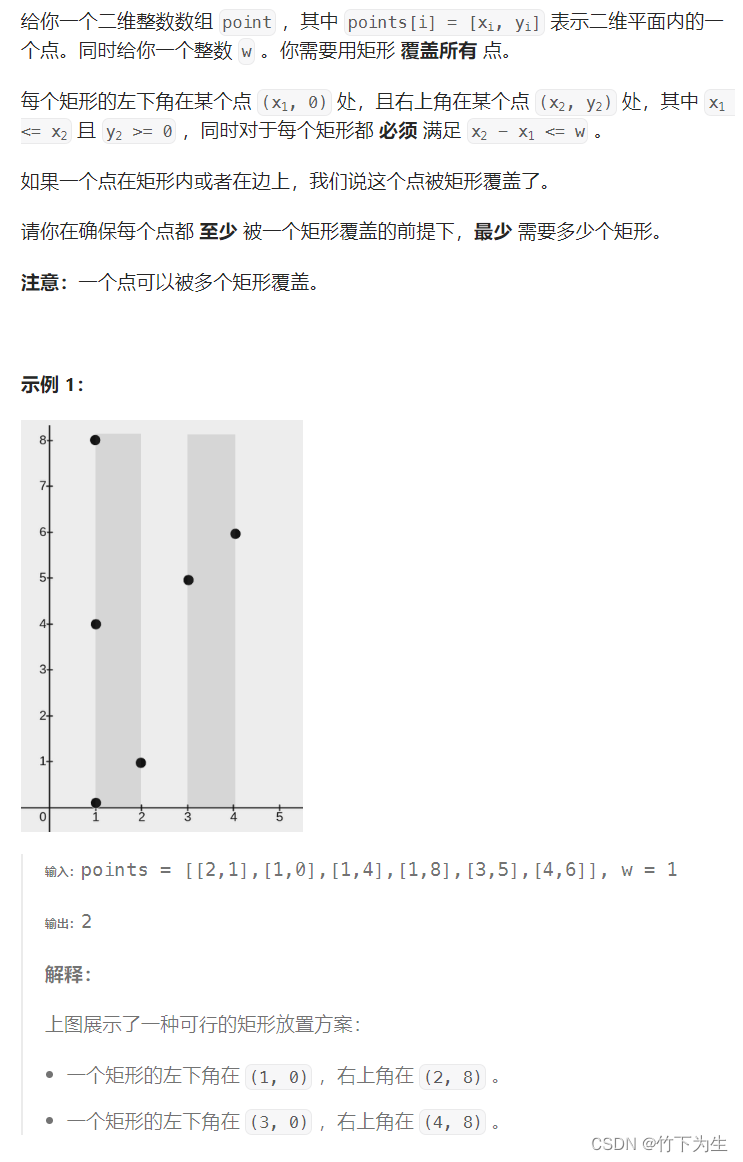
题目没有限制矩阵的高度，我们只要关心矩阵宽度<=w即可，代码如下

class Solution {
public:
    int minRectanglesToCoverPoints(vector<vector<int>>& points, int w) {
        int n = points.size();
        sort(points.begin(),points.end());
        int ans = 0;
        for(int i=0;i<n;){
            int j = i++;
            while(i<n&&points[i][0]-points[j][0]<=w)
                i++;
            ans++;
        }
        return ans;
    }
};

三、访问消失结点的最少时间

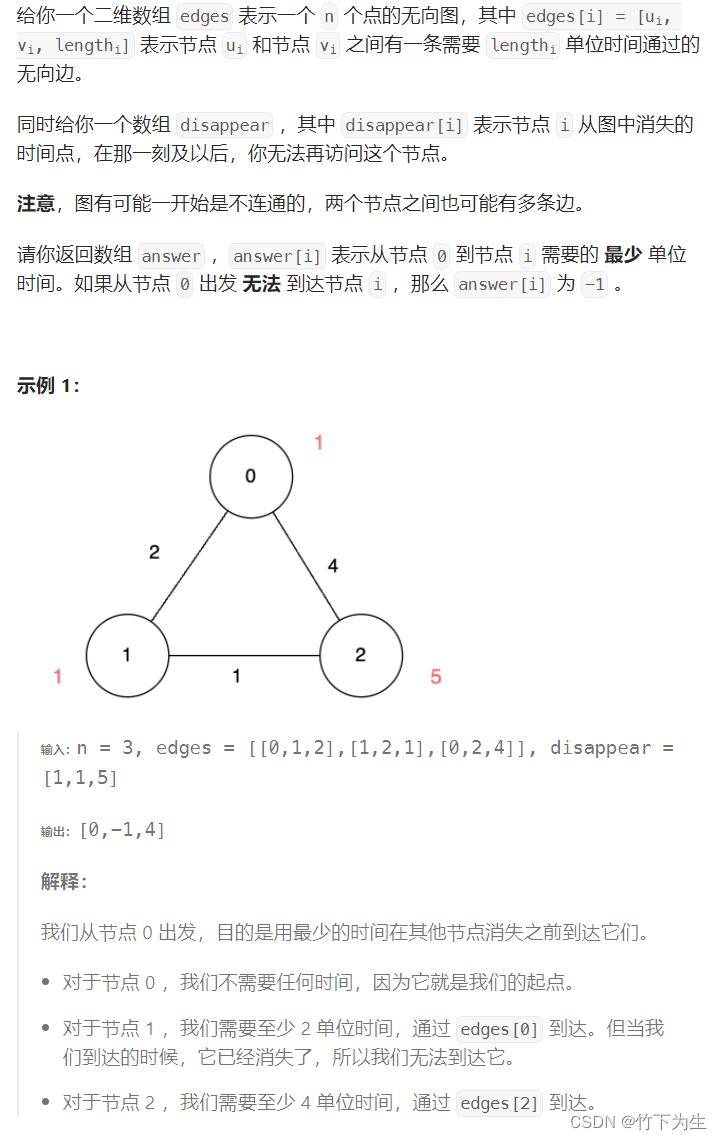
这题抛开消失的结点这一条件后，就是单纯的迪杰斯特拉算法求到单源结点的最短路径问题，所以这题的核心就是对迪杰斯特拉算法进行变形。这里的变形也很简单，就是再更新最短路径的时候，也要判断当前结点是否已经消失，如果消失同样无法更新。

简单介绍一下迪杰斯特拉算法的步骤(适用于边权>=0)：

需要三个数组

• dist[n] --- 记录vi - v0 的最短路径，初始化为无穷大
• parent[n] --- 记录vi的上一个结点 ，用来回溯vi到v0所需要经过的结点，初始化为-1
• vis[n] --- 记录结点的最短路径是否已经被计算过，初始化为false

其中parent不是计算最短路径长度所必须的，如果不需要得到具体路径，可以不要

算法的执行过程如下

代码如下

class Solution {
public:
    vector<int> minimumTime(int n, vector<vector<int>>& edges, vector<int>& disappear) {
        vector<vector<pair<int,int>>>g(n);
        for(auto v:edges){
            int x = v[0], y = v[1], w = v[2];
            g[x].emplace_back(y,w);
            g[y].emplace_back(x,w);
        }
        vector<int> dist(n,INT_MAX);
        // 用优先级队列(堆)优化算法
        priority_queue<pair<int,int>>pq; // [d,i]
        pq.emplace(0,0);
        dist[0] = 0;
        while(pq.size()){
            auto [d,i] = pq.top();pq.pop();
            if(dist[i]!=-d) continue; // 懒更新
            for(auto [x,w]:g[i]){
                if(dist[i]+w < dist[x] && dist[i]+w < disappear[x]){ // 注意结点的消失时间
                    dist[x] = dist[i]+w;
                    pq.emplace(-dist[x],x);
                }
            }
        }
        for(auto&e:dist){
            if(e==INT_MAX)
                e = -1;
        }
        return dist;
    }
};

 四、边界元素是最大值的子数组数目

这题题目看完之后，没思路先看看给的样例，去手动模拟一下，很容易就会发现，如果出现一个很大的数字，那么它左边的数字就没法在和它右边的数字组成符合条件的子数组了，也就是说前面的数字无用了，一般这种会导致元素失效的，可以往单调栈和单调队列上去思考，这题就能用单调栈来做，具体思路如下：

遍历数组，我们维护一个单调递减的栈，栈中记录元素大小和元素出现的次数，如果遇到比栈顶元素大的数，将栈顶元素pop，因为它无法在和当前位置右边的数再组成合法的子数组了，直到当前栈顶元素大于/等于nums[i]，然后判断是否等于，如果等于，更新答案和该元素出现次数，如果大于，直接让元素入栈，代码如下

class Solution {
public:
    long long numberOfSubarrays(vector<int>& nums) {
        int n = nums.size();
        long long ans = n;
        stack<pair<int,int>>st;
        for(int i = 0; i < n; i++){
            while(st.size()&&nums[i]>st.top().first){
                st.pop();
            }
            if(st.size()&&st.top().first==nums[i]){
                ans+=st.top().second++;
            }else{
                st.emplace(nums[i],1);
            }
        }
        return ans;
    }
};