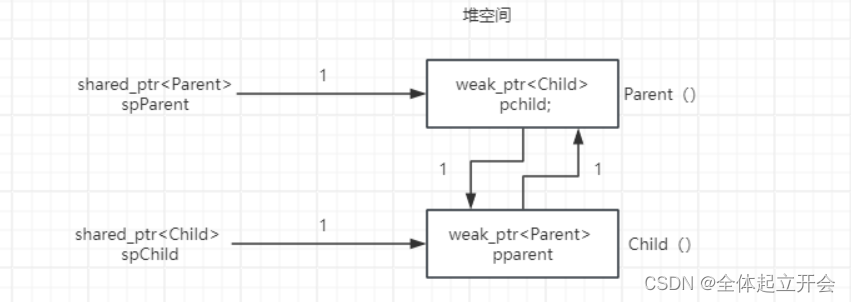
Basic radiometry (辐射度量学)

光的强度假定l为10,但是10是什么。
Whitted-Style中间了很多不同简化,如能看到高光,表示做了布林冯着色,意味着一个光线打进来后会被反射到一定的区域里,而不是沿着完美的镜像方向,但我们假设的是完美的反射。折射同理。其中能量的损失没有计算,可以是自己定的一个数量。
辐射度量学,会精确的把光的物理量定义出来。

辐射度量学表示如何描述光照。
会给光定义各种不同的属性(表示光在空间中的属性),仍然是基于几何光线,即直线传播,没有波动性
物理量:Radiant flux,intensity,irradiance,radiance
Radiant Energy and Flux (Power)

Radiant energy是电磁辐射的能量,单位焦耳。光源辐射出来的就是能量
Radiant flux是单位时间的能量。即单位能量除于单位时间,其实是功率,单位瓦特。热学上叫流明
在这个辐射度量的体系中,考虑的都是单位时间的性质
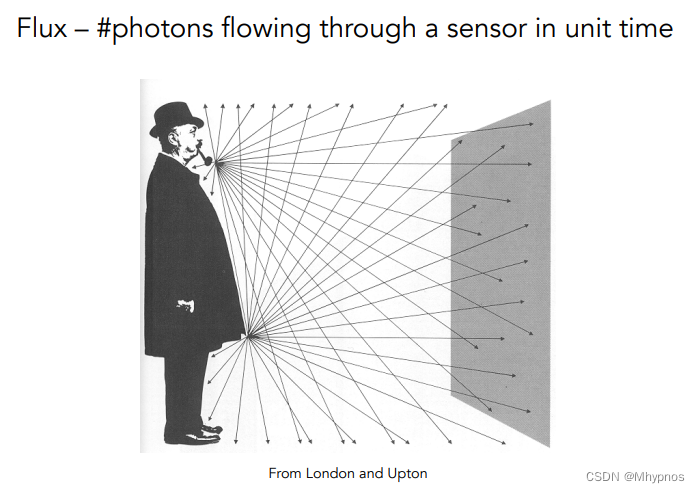
假设平面是一个感光的东西,给单位的时间,通过的光子数量就是Flux。
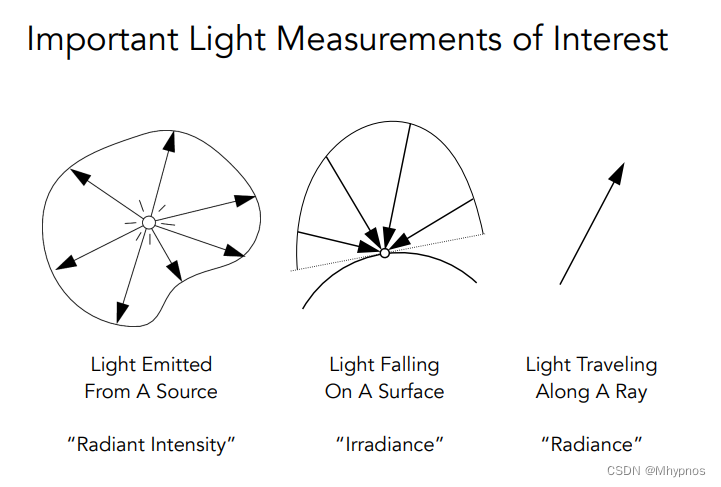
Radiant Intensity:光源会发出多少能量
Irradiance:任何一个物体表面会接收到多少能量
Radiance:光线传播过程中的能量定义
Radiant Intensity
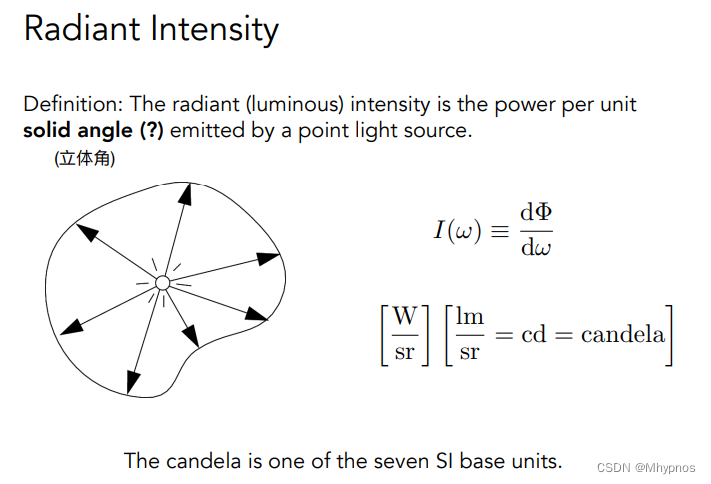
能量除以立体角, 单位是【瓦/sr】
angle

角度定义:用弧l除以半径r。
整个圆的角就是周长除以半径 ,2Π弧度
立体角:在3维空间中,找某一个球,从球出发,形成有一定大小的锥,锥会打到球面上,形成一定大小的面积。立体角就是球面上的面积A除以半径的平方
整个球面的立体角就是球面面积除以半径平方,4Π
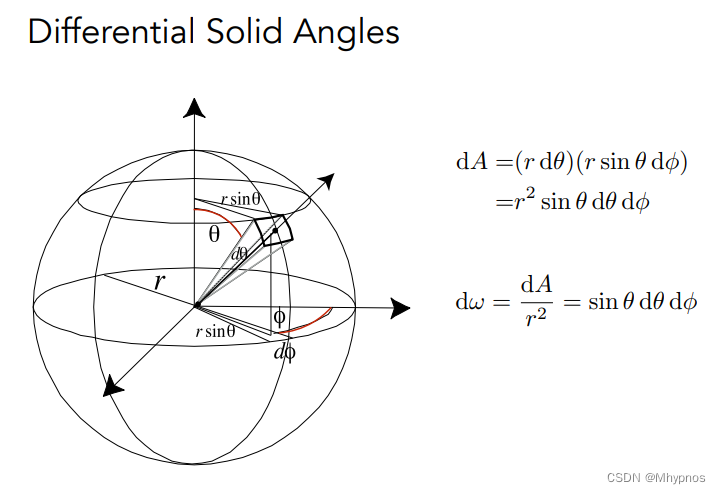
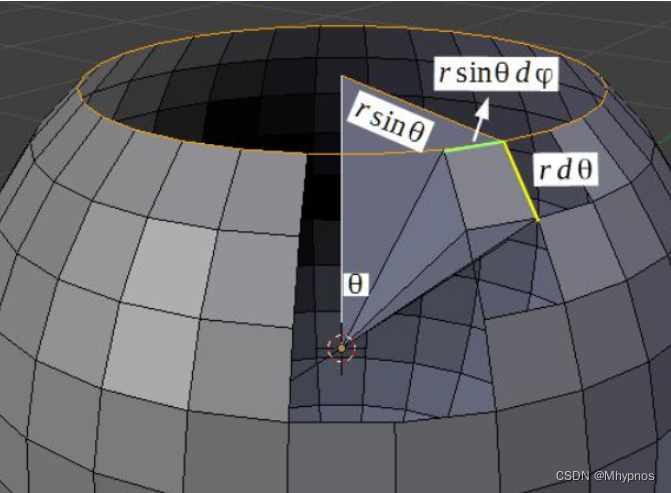
单位立体角/微分立体角:定义一个方形的面积。θ是方向离z轴正方向的夹角,Φ是绕z轴旋转的角度。可以看出横边是rsinθdφ,竖边是rdθ。
θ和Φ并不是对球面积均匀的划分,因为前面还有sinθ,极点和赤道是不一样的
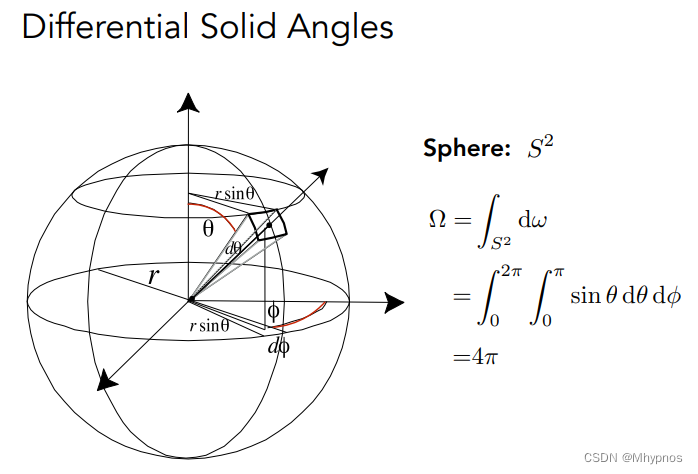
单位立体角是4Π
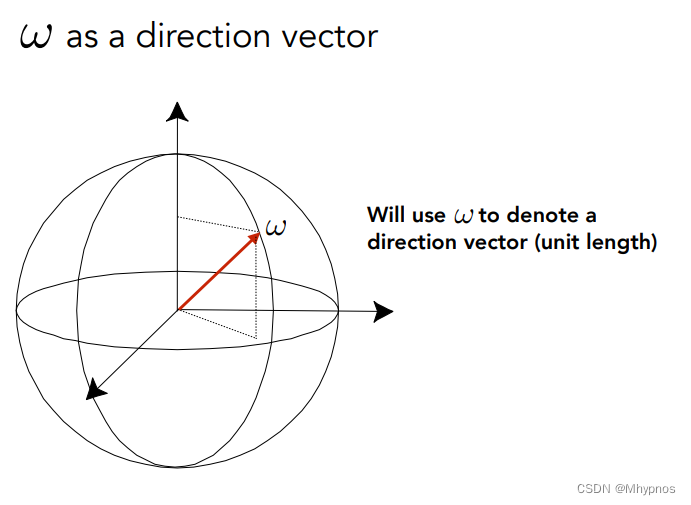
表示3维空间的方向是通常用ω表示,用φ,θ来定义位置。并且用sinθdθdφ来算出微分立体角(单位立体角)
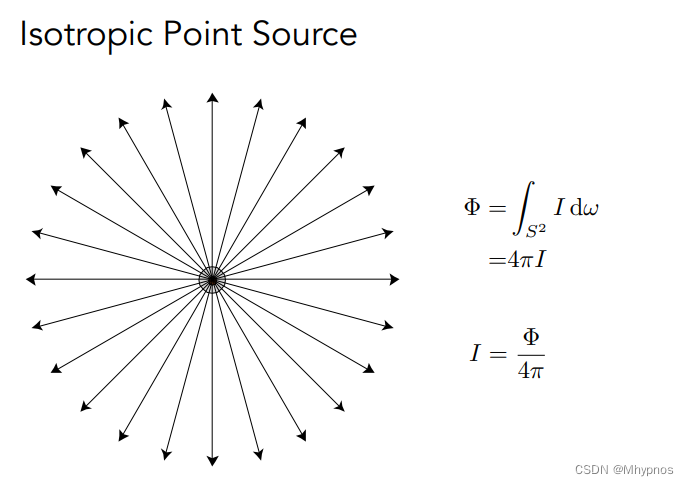
Intensity的定义就是光源在任何一个方向上的亮度,总共的亮度是flux,除以单位立体角。等于从任何方向上看到的亮度。
如果一个点光源是往各个方向均匀的辐射能量,则任何一个方向上对应的Intensity就是power除以4Π。得到方向上的对应的强度

815流明对应11瓦。则815/4Π就是65candelas,对应某方向上的Intensity

图形学里基本不用实际能量,用的各种能量都是单位时间的,瓦
Intensity:一个立体角上的能量
立体角:单位面积除以球的半径平方
Irradiance

Irradiance :每个面积上对应的能量,注意与Intensity区分(每个立体角上对应的能量)。面必须和入射光线垂直

Irradiance定义的是投影方向上/垂直于光线的面积

阳光始终垂直于某一区域,接收的能量多

可以定义点光源的功率φ,认为往周围各个方向是均等辐射出能量。Irradiance是单位面积的接收能量。如上图内圈
r
r
r为1,面积是
4
π
r
2
4{\pi}r^2
4πr2, φ 除以
4
π
r
2
4{\pi}r^2
4πr2就是对应面积的能量E,
远处的能量
E
‘
E^`
E‘对比
E
E
E即为
E
r
2
{E}\over{r^2}
r2E
Irradiance在衰减,Intensity实际上没有衰减
Radiance

Radiance是为了描述光线的属性

Radiance定义power在单位立体角,并且在单位投影面积。两次微分
确定一个区域,一个单位面积有个朝向,从这个面往某个方向辐射一些能量

Radiance可以理解为每个立体角的Irradiance,或者每个单位面积的Intensity

Irradiance是dA接收到的能量
一个
ω
\omega
ω方向打到一个面上,到达这个面时的能量就是Radiance。如果考虑四面八方收到的能量就是dA整个收到的能量Irradiance,但是只考虑一个方向进来被dA接收的能量就是Radiance,也就是Irradiance在
ω
\omega
ω方向上的分量。

Intensity是每一个立体角上的能量,dA往每一个确定的立体角
ω
\omega
ω有多少的Intensity,辐射出的能量就是Radiance

Irradiance是某个范围dA收到的所有能量,对应Radiance也是某个小范围dA,但只考虑某个方向上收到的能量
Bidirectional Reflectance Distribution Function(BRDF)
双向反射分布函数
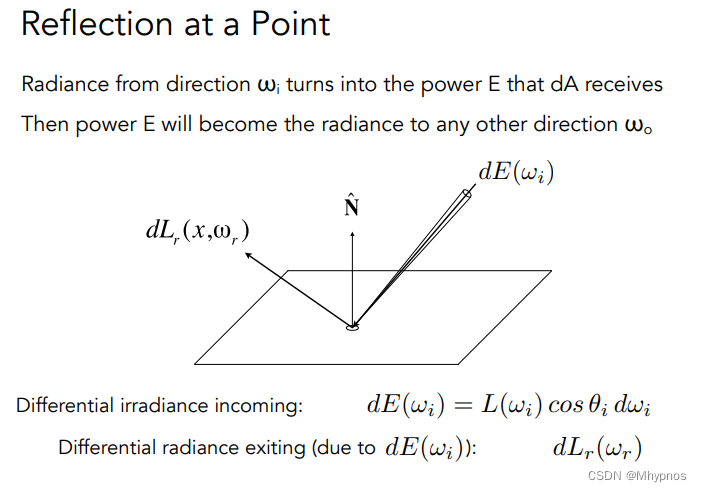
需要有一个函数来描述从某个方向进来,并且到某个方向去的能量是多少。
反射:光打到一个物体,然后被弹走。另一种理解,光线打到了某一物体表面被吸收了,然后再从这个物体表面被发出去。
从某一立体角进来,打到一个小的表面
d
A
dA
dA
从
ω
i
\omega_i
ωi来的radiance
L
L
L,会打到
d
A
dA
dA上,radiance 本身考虑的是每立体角每单位面积。现在限制了单位面积收到的立体角能量,会被小的范围被吸收,吸收了多少,再原样的发出去。
入射的radiance会在单位面上转换成能量power,然后power又会辐射到另一个方向去
对于小的块,单考虑某一个方向上接收到的能量,就是某一个方向上的立体角
d
ω
i
d\omega_i
dωi的radiance
L
ω
i
L\omega_i
Lωi和
c
o
s
θ
i
cos\theta_i
cosθi乘积得到的就是irradiance,
irradiance在转化成radiance辐射出去

现在不知道往某个方向辐射出的能量是多少,因此定义一个函数专门来描述:微小面积
d
A
dA
dA从某一个微小立体角
d
ω
i
d\omega_i
dωi接收到的irradiance,会如何被分配到各个立体角上去。这里其实就是一个比例:出射方向radiance除以接收到的irradiance就是BRDF的定义。告诉我们如何把收集到的能量反射到另一个方向上去,即定义如何去分配
反射是两部分,第一入射光会让
d
A
dA
dA收到一个irradiance,即入射光的radiance乘以对应方向的立体角就是给
d
A
d A
dA的irradiance是多少。上述式子是把关系展开。
BRDF就是从一个方向进来,打到某一个物体后,往不同的方向反射,它的能量分布
如果是镜面反射说明反射的方向上分布了所有能量,只要不是镜面反射方向没有任何能量
如果是漫反射,则进来的能量会被均等的分配到各个方向
BRDF的概念就是描述光线和物体是如何作用的,因此BRDF定义了物体的不同材质

某个着色点, 可以接收四面八方不同方向的光照。可以考虑对于每个入射方向,都会对应入射方向,着色点和出射方向这样的一个BRDF。BRDF会告诉从某个入射方向进来的光反射到某个出射方向有多强。
则把每一个入射方向的入射光强度(radiance)乘以BRDF乘以cos角立体角,然后把每一个入射方向对于出射方向的贡献加起来,就可以得到这个着色点在所有可 能的入射方向最后反射到出射方向时看到的样子
反射方程定义了,任何一个着色点,在各种不同的光照环境下,考虑任何一个光照的进入方向对我观测方向/出射方向的贡献,把所有贡献加起来得到该着色点的样子

反射方程需要我们考虑所有能够到达对应着色点的光线,这些光线不仅来自光源,还可能来源于别的物体经过一次反射后出去的radiance。即任何出射的radiance都有可能作为其他点入射的radiance,所以是一个递归的计算方式
渲染方程/绘制方程

如果一个物体会发光,则需要把物体本身的光源强度加上。即渲染方程
渲染方程里把
c
o
s
θ
cos\theta
cosθ写成法线
n
⃗
\vec n
n点乘入射方向$
d
ω
i
d\omega_i
dωi
通过这一个方程可以描述所有的光线传播

一个点光源的情况,反射光。 自己发射的光。 入射光。 BRDF。 夹角

多个点光源,遵循线性性质,加起来即可

面光源:一堆点光源的集合。如果可以把一堆点光源的贡献加起来,那同理可以把面光源上任意一个点的贡献积分起来。
积分面光源所占据的立体角,考虑所有覆盖的方向,入射进来的radiance经过BRDF反射出去的贡献。
即对于多个点光源由求和变成积分

其他物体反射的radiance作为入射光,同样的考虑物体覆盖的立体角过来的radiance是多少。等于把物体的反射面当成一个光源

渲染方程使用例子

从某个方向看向点的值需要解,从其他物体反射到点的值也需要解,其他值是已知的。
简化的式子:位置+角度 这两个变量用一个概括,变成u以及v

更近一步简写:对所有物体辐射出来的所有能量等于所有光源辐射出来的能量加上辐射出来的能量被反射之后的能量
把方程写成算子的形式
K理解成反射操作符

利用算子的运算性质(求逆以及泰勒展开)来解方程,解出L

对光线弹射次数的分解,看到的光线不弹射(光源),弹射一次(直接光照),弹射两次(间接光照)。。。
所有不同弹射次数的光线加起来就是全局光照

光栅化着色的就是直接光照或者光源自己,即弹射0次或者1次

直接光照

一次间接光照,光线弹射两次


弹射更多次的全局光照
对比上图弹射3次与4次更多的顶部玻璃吊饰
光线只弹射3次的话,只够从摄像机进入到物体,但出不来。如一个玻璃球,弹射两次才出来,对于一个双层的玻璃,经过两次弹射只能进去,再经过两次弹射,才出来


8次,16次亮度变化没有那么明显了
无限次数的光线弹射后,会收敛到某一种亮度,不再出现特别剧烈的变化
对于相机的快门,一直开着,会出现过曝的问题,因为定义辐射度量学时要考虑能量,考虑单位时间。一直按快门,积累的能量是越来越长的
Probability Review

随机变量X
随机变量的分布 p(X)变量出现的机率

概率非负,所有概率相加为1

期望:不断取随机变量,求平均

连续情况下的概率,取微小的一段对应的梯形面积,y坐标并不是表示概率,而是一个点取周围一定的值,左边界右边界连线形成的区域是概率
曲线称为概率密度函数PDF
函数下方整个的面积即把概率密度函数按照x积分起来,为1
期望:任何一个取值x乘以概率密度并且积分起来

一个随机变量X的函数Y,Y的期望就是f(x)*p(x)并且积分









![[阅读笔记20][BTX]Branch-Train-MiX: Mixing Expert LLMs into a Mixture-of-Experts LLM](https://img-blog.csdnimg.cn/direct/8751e7253f134d69b3387fceb546fff5.png)