给定整数 n ，返回 所有小于非负整数 n 的质数的数量 。

示例 1：

输入：n = 10
输出：4
解释：小于 10 的质数一共有 4 个, 它们是 2, 3, 5, 7 。

示例 2：

输入：n = 0
输出：0

示例 3：

输入：n = 1
输出：0

提示：

• 0 <= n <= 5 * 10^6

---

埃氏筛（又称埃拉托斯特尼筛法）是一种用于寻找小于等于给定整数 n 的所有质数的算法。

该算法的工作原理如下：

1. 创建一个布尔数组 isPrime，其中 isPrime[i] 表示数字 i 是否是质数。
2. 将 isPrime[0] 和 isPrime[1] 设置为 false，因为 0 和 1 不是质数。
3. 从 2 开始，遍历所有数字 i。
4. 如果 isPrime[i] 为 true，则 i 是一个质数。
5. 将所有 i 的倍数 j 标记为非质数（即 isPrime[j] = false）。
6. 继续步骤 3，直到遍历完所有数字。

针对本题有一些适配变化，比如不关心0和1的状态，以及求的是小于n的质数的数量，所以  n = 2时答案也是0。

class Solution {
public:
    int countPrimes(int n) {
        int count = 0;
        vector<int> isPrime(n,1);
        for(int i = 2;i < n;i++){
            if(isPrime[i]){
                count++;
                for(int j =  2 * i;j < n;j += i){
                    isPrime[j] = 0;
                }
            }
        }
        return count;   
    }
};

这里有几个可以优化的点：

1. 除了2以外的偶数一定不是质数。
2. 从x^2开始标记即可，因为2x，3x一定在之前就被标记过了，比如2的倍数标记2x。

class Solution {
public:
    int countPrimes(int n) {
        if(n <= 2) return 0;
        int count = 1;
        vector<int> isPrime(n,1);
        for(int i = 3;i < n;i += 2){
            if(isPrime[i]){
                count++;
                for(long long j = (long long) i * i;j < n;j += 2 * i){
                    isPrime[j] = 0;
                }
            }
        }
        return count;   
    }
};

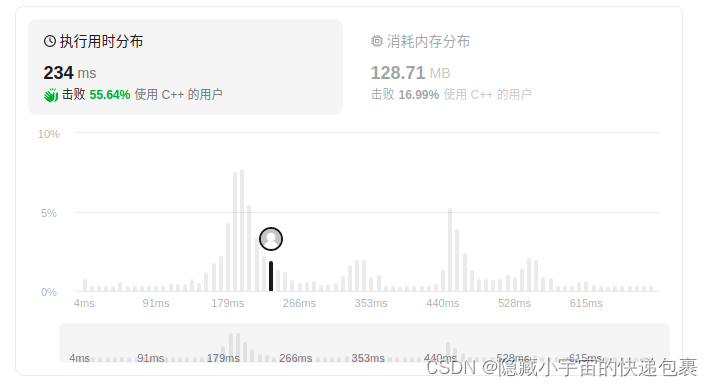
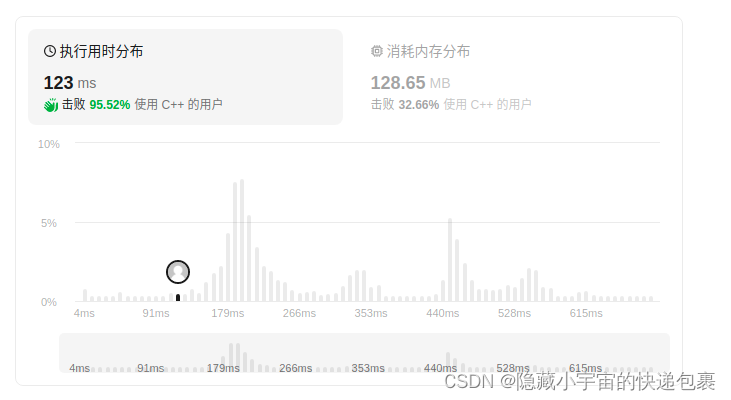
优化前后时间对比：