代码随想录算法训练营Day4 | 24.两两交换链表中的节点、19删除链表中的第N个节点、链表相交、142.环形链表

news2025/1/12 5:58:41

24.两两交换链表中的节点

题目：给你一个链表，两两交换其中相邻的节点，并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题（即，只能进行节点交换）。

题目链接：24. 两两交换链表中的节点

卡哥的视频讲解：帮你把链表细节学清楚！ | LeetCode：24. 两两交换链表中的节点

题目思考：定义一个虚拟头节点，对该节点后的两个节点进行操作，注意判断可循环条件以及定义变量来暂时储存节点。

交换过程如图：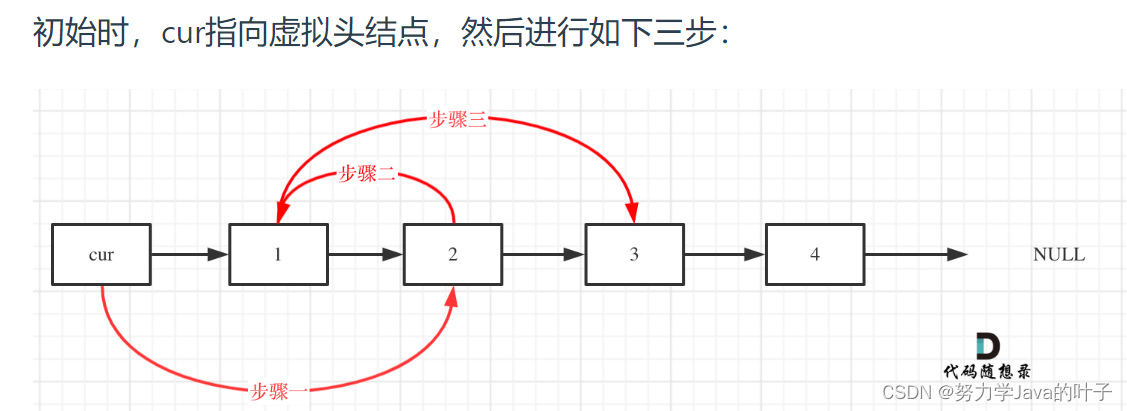

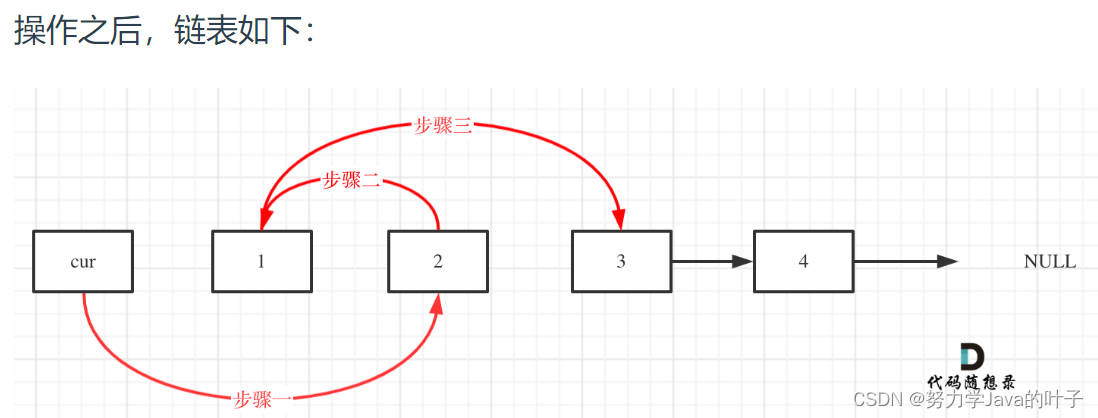
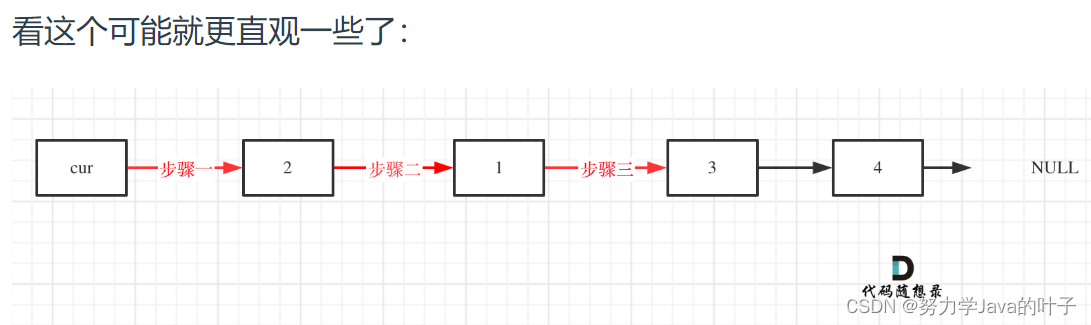
代码示例：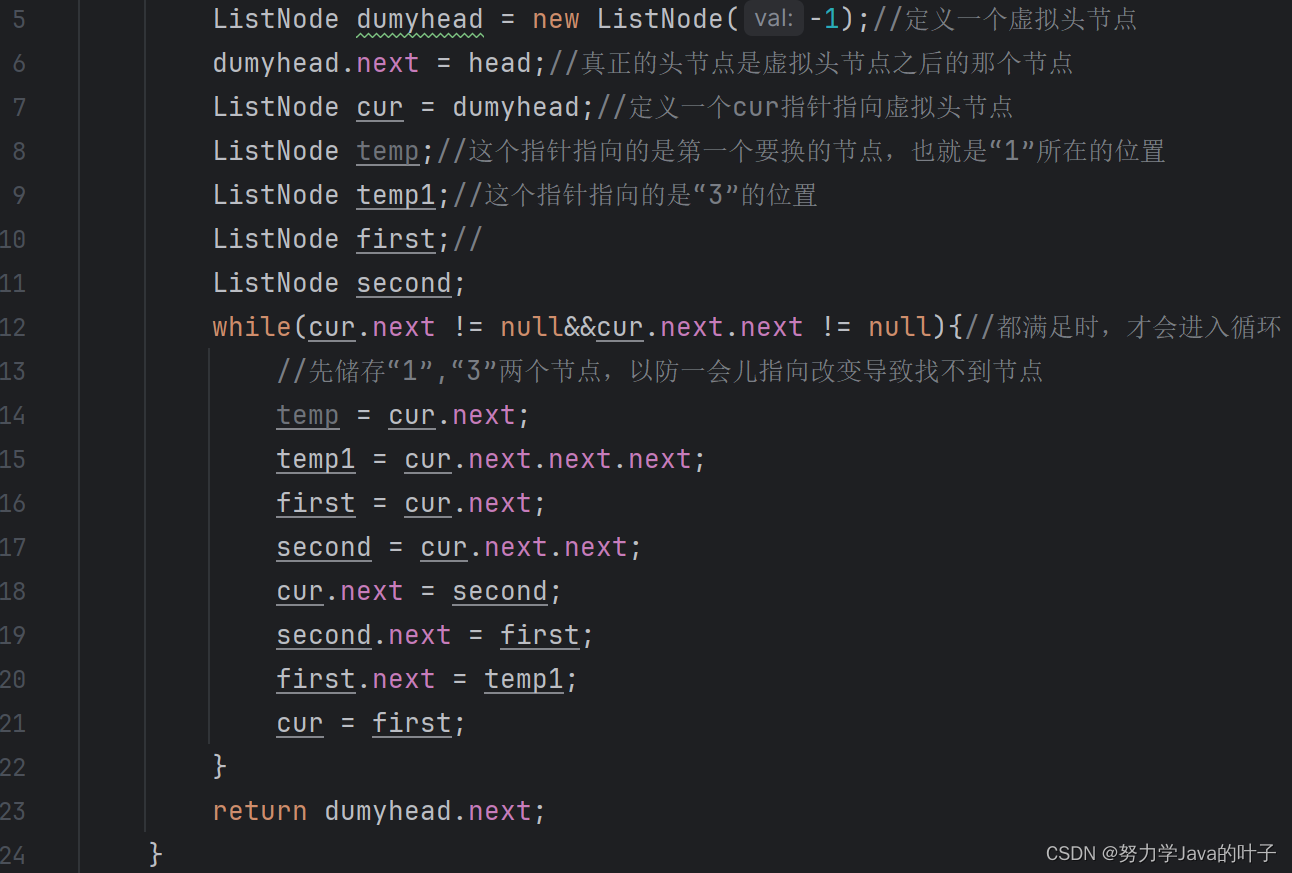

代码逻辑详解：

首先创建一个虚拟头节点 dumyhead，值为 -1，并将其指向链表的头节点 head。这样做是为了处理头节点的特殊情况。
创建指针 cur 指向虚拟头节点 dumyhead，用于遍历链表。
创建临时指针 temp 用于指向待交换节点的前一个节点，即第一个要交换的节点的前一个节点。
创建临时指针 temp1 用于指向待交换节点的后一个节点的后一个节点，即第二个要交换的节点的后一个节点。
创建两个指针 first 和 second 分别指向待交换的两个节点。
进入循环，条件是 cur.next 和 cur.next.next 都不为 null，即链表中至少有两个节点。这样做是为了保证交换的两个节点是相邻的。
在循环中，首先保存好要交换的两个节点及其前后节点的位置，以便后续指针操作。
将 cur.next 指向第二个节点 second，即将第二个节点提前。
将 second.next 指向第一个节点 first，完成交换。
将 first.next 指向之前保存的 temp1，即将第一个节点的下一个节点指向原来第二个节点的后一个节点。
将 cur 指向交换后的第一个节点，为下一轮交换做准备。
循环结束后，返回虚拟头节点的下一个节点，即交换后的链表的头节点。

这样，整个链表中相邻节点的交换就完成了。

leetcode提交记录：

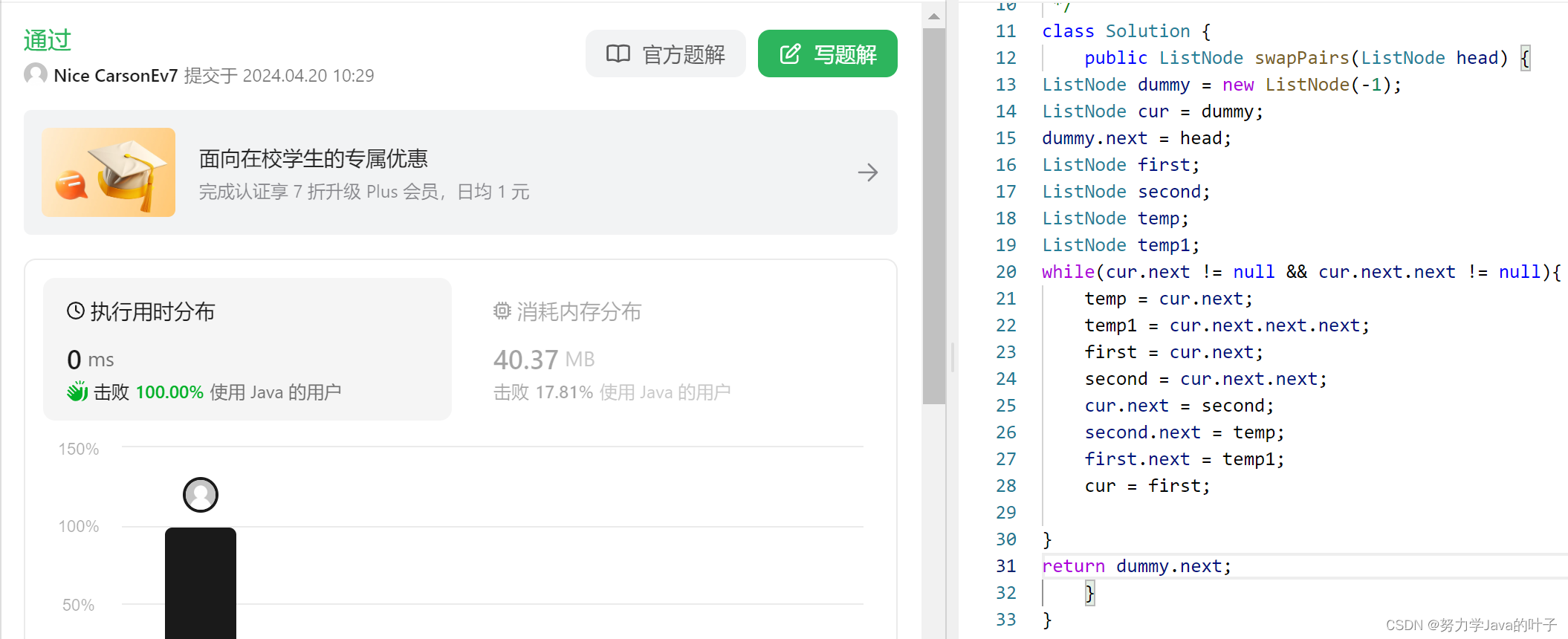
小tips：

1.先把节点交给指针之后，再进行交换，别忘了设置两个temp值

2.注意循环的条件，这里巧妙地将链表个数为偶数和奇数的情况都囊括了，当链表个数为偶数时，如果cur的下一个为空，则停止循环，如果链表个数为奇数时，则还需要同时满足cur下一个的下一个为空才会停止循环，这也是为什么只能用和而不能用或。注意！！

cur.next != null&&cur.next.next != null
这两个条件的顺序不能调换，否则会报空指针异常的错误。

19.删除链表的倒数第N个节点

题目：给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

题目链接：19. 删除链表的倒数第 N 个结点

卡哥的视频链接：链表遍历学清楚！ | LeetCode：19.删除链表倒数第N个节点

题目思考：要找到删除的节点，就要知道它的上一个节点是什么，我开始的想法是把链表反转过来，直接删除第n个节点，但是这个操作就复杂了，可以直接使用快慢指针。假如要删除倒数第n个节点，则让快指针先走n+1步（+1是为了让慢指针指向被删除节点的前一个），再让快慢指针同时走，当快指针指向空时，慢指针就走到被删除节点的前一个了。（如下图）

代码示例：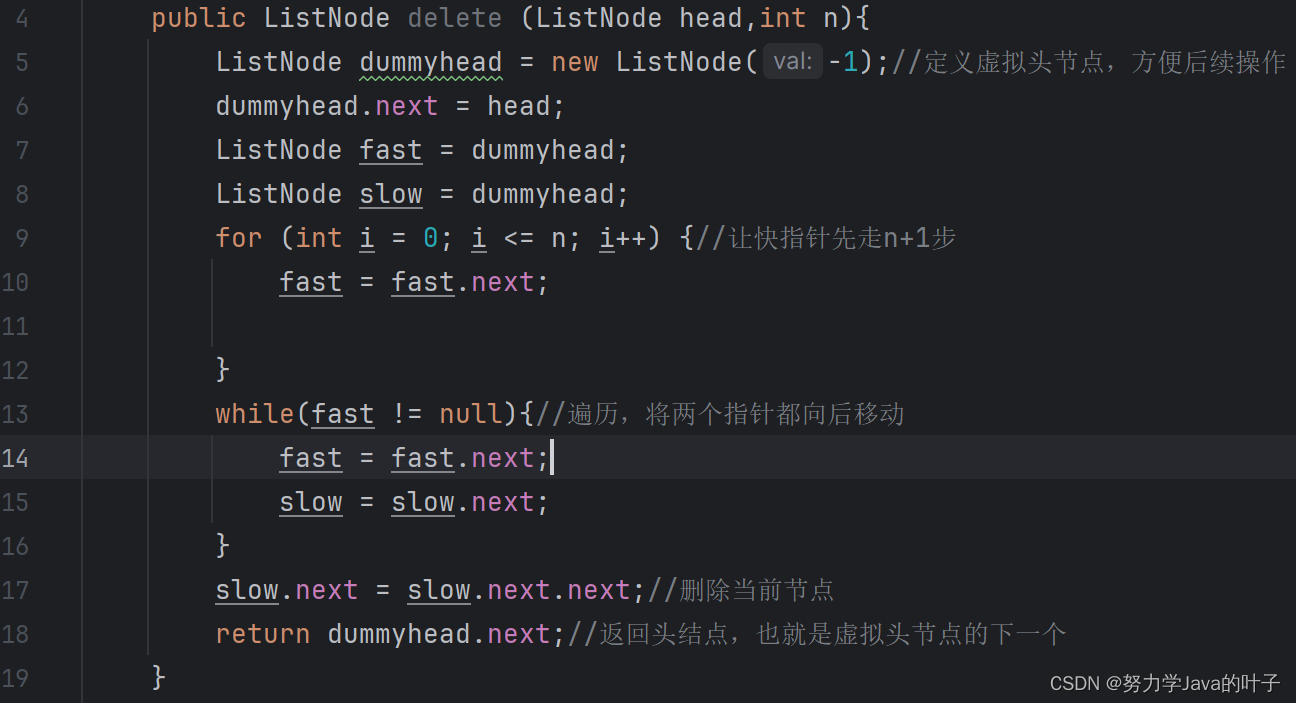

代码详细逻辑：

首先创建一个虚拟头节点 dummyhead，值为 -1，并将其指向链表的头节点 head。这样做是为了处理删除头节点的特殊情况。
创建两个指针 fast 和 slow，都指向虚拟头节点 dummyhead。fast 指针先向前移动 n+1 步，使其与 slow 指针相隔 n 个节点。
进入循环，条件是 fast 指针不为 null。在循环中，fast 指针和 slow 指针同时向前移动，直到 fast 指针指向 null，即到达链表的末尾。
循环结束后，slow 指针指向要删除节点的前一个节点，而 fast 指针指向要删除节点的后一个节点。
将要删除节点的前一个节点 slow 的 next 指针指向要删除节点的下一个节点，从而将要删除的节点从链表中删除。
返回虚拟头节点的下一个节点，即删除节点后的链表的头节点。