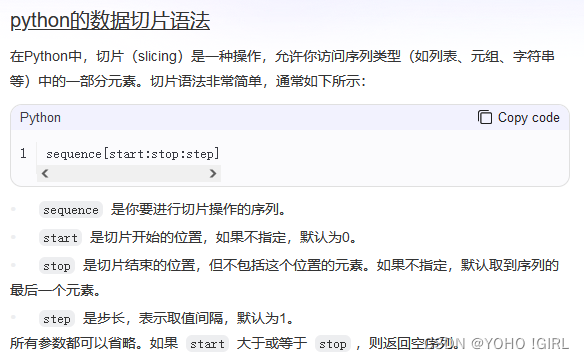
IMU&GNSS的误差状态卡尔曼滤波器(ESKF)的数学模型
把IMU视为运动模型,把GNSS观测视为观测模型,推导整个滤波器
设状态变量为
x
=
[
p
,
v
,
R
,
b
g
,
b
a
,
g
]
T
x=[p,v,R,b_{g},b_{a},g]^{T}
x=[p,v,R,bg,ba,g]T
所有变量都默认取下标WB,即机器人在世界坐标系下的变量。
变量依次为:平移、速度、旋转、陀螺仪零偏、加速度计零偏、重力
将IMU测量值带入IMU运动方程中,状态变量在连续时间下的运动方程为
p
˙
=
v
v
˙
=
R
(
a
~
−
b
a
−
η
a
)
+
g
R
˙
=
R
(
ω
~
−
b
g
−
η
g
)
∧
b
g
˙
=
η
b
g
b
a
˙
=
η
b
a
g
˙
=
0
\begin{matrix} \\\dot{p} =v \\\dot{v} = R(\tilde{a}-b_{a}-\eta_{a})+g \\\dot{R} =R(\tilde{\omega}-b_{g}-\eta_{g})^{\wedge } \\\dot{b_{g}} =\eta_{bg} \\\dot{b_{a}} =\eta_{ba} \\\dot{g} = 0 \end{matrix}
p˙=vv˙=R(a~−ba−ηa)+gR˙=R(ω~−bg−ηg)∧bg˙=ηbgba˙=ηbag˙=0
为了在EKF的预测过程中对协方差进行预测,需要对该方程进行线性化。
理论上,线性化的形式为
x
k
+
1
=
f
(
x
k
)
+
F
d
x
+
w
x_{k+1}=f(x_{k})+Fd_{x}+w
xk+1=f(xk)+Fdx+w
其中, F = ∂ f ∂ x ( t ) ∣ x ( t ) F=\frac{\partial_{f} }{\partial_{x(t)}} |_{x(t)} F=∂x(t)∂f∣x(t)为系数矩阵。该矩阵由运动方程和各项状态变量的导数构成。
F中需要计算旋转矩阵R相对于某个扰动的导数,而在不引入张量的情况下,是无法表达矩阵对向量导数的形式的。传统算法往往会退一步,用欧拉角或者四元数的四个标量作为状态量,但这样就无法使用流形上的方法了。如果考虑将惯性导航与卫星导航进行融合,那么x中的平移变量就应该使用全局坐标系。这会使x中的数值变的很大,在有些场合超出浮点数的有效数字范围。
能否避免直接使用x和P来表达状态的均值和协方差,推导运动和观测方程呢?能否使用原先卡尔曼滤波器中的更新量来推导这两个方程?
卡尔曼滤波器中的观测部分为:
x
k
=
x
k
,
p
r
e
d
+
K
k
(
z
k
−
H
k
x
k
,
p
r
e
d
)
x_{k}=x_{k,pred}+K_{k}(z_{k}-H_{k}x_{k,pred})
xk=xk,pred+Kk(zk−Hkxk,pred)
其中
(
z
k
−
H
k
x
k
,
p
r
e
d
(z_{k}-H_{k}x_{k,pred}
(zk−Hkxk,pred 为更新量,应是位于切空间中的矢量,中间的加法应为流形与切空间指数映射的广义加法。
但也可以将更新量(或者称为误差状态)视为滤波器的状态变量,来推导运动和观测模型。
不光是平移和旋转,把所有的状态都用误差状态来表达,这就是典型ESKF的做法。
相比于传统的KF,ESKF的优点如下:
- 在旋转的处理上,ESKF的状态变量可以采用最小化的参数表达,也就是使用三维变量来表达旋转的增量。该变量位于切空间中,而切空间是一个矢量空间。传统KF需要用到四元数(4维)或者更高维的变量来表达状态(旋转矩阵,9维),要不就得采用带有奇异性的表达方式(欧拉角)。
- ESKF总是在原点附件,离奇异点较远,数值方面更稳定,并且不会产生离工作点太远而导致线性化近似不够的问题
- ESKF的状态量为小量,其二阶变量相对来说可以忽略。同时,大多数雅可比矩阵在小量情况下变的非常简单,设置可以用单位阵代替。
- 误差状态的运动学相比原状态变量更小(小量的运动学),因此可以把更新部分归入原状态变量中。
在ESKF中,通常把原状态变量称为名义状态变量(Nominal State),把ESKF里的状态变量称为误差状态变量(Error State)。名义状态变量和误差状态变量之和称为真值。
把噪声的处理放到误差状态变量中,可以认为名义状态变量的方程是不含噪声的。
将噪声分离后,名义状态变量的方程变得简洁。滤波器仅需考虑误差状态如何运动,如何观测,最后如何滤波,和名义状态的关系不大。
ESKF的整体流程如下:
当IMU测量数据到达时,把它积分后,放入名义状态变量中。由于这种做法没有考虑噪声,其结果自然会快速漂移,于是把误差部分作为误差变量。
在运动过程中,名义状态随着IMU数据进行递推,误差状态则受到高斯噪声影响而变大。
此时,ESKF的误差状态均值和协方差会描述误差状态扩大的具体数值(视为高斯分布)。
ESKF的更新过程需要 依赖IMU以外的传感器观测。更新过程中,利用传感器数据,更新误差状态的后验均值与协方差。
随后可以把这部分误差合入名义状态变量中,并把ESKF置零,这样就完成了一次预测——更新的循环。
推导ESKF的两个过程。设ESKF的真值状态为
x
t
=
[
p
t
,
v
t
,
R
t
,
b
g
t
,
b
a
t
,
g
t
]
T
x_{t}=[p_{t},v_{t},R_{t},b_{gt},b_{at},g_{t}]^{T}
xt=[pt,vt,Rt,bgt,bat,gt]T。下标t表示true,即真值状态。
这个状态随时间改变,可以记作
x
t
(
t
)
x_{t}(t)
xt(t)。在连续时间上,记IMU读数为
ω
~
,
a
~
\tilde{\omega} ,\tilde{a}
ω~,a~,那么可以写出状态变量导数相对与观测量之间的关系为:
p
t
˙
=
v
t
v
t
˙
=
R
(
a
~
−
b
a
t
−
η
a
)
+
g
R
t
˙
=
R
(
ω
~
−
b
g
t
−
η
g
)
∧
b
g
t
˙
=
η
b
g
b
a
t
˙
=
η
b
a
g
t
˙
=
0
\begin{matrix} \\\dot{p_{t}} =v_{t} \\\dot{v_{t}} = R(\tilde{a}-b_{at}-\eta_{a})+g \\\dot{R_{t}} =R(\tilde{\omega}-b_{gt}-\eta_{g})^{\wedge } \\\dot{b_{gt}} =\eta_{bg} \\\dot{b_{at}} =\eta_{ba} \\\dot{g_{t}} = 0 \end{matrix}
pt˙=vtvt˙=R(a~−bat−ηa)+gRt˙=R(ω~−bgt−ηg)∧bgt˙=ηbgbat˙=ηbagt˙=0
这里把重力g考虑进来的主要理由是方便确定IMU的初始姿态。
如果不在状态方程里写出重力变量,那么必须事先确定初始时刻的IMU朝向R(0),才可以执行后续的计算。此时,IMU的姿态是相对与初始的水平面来描述的。
如果把重力写出来,就可以设IMU的初始姿态为单位阵,把重力方向作为IMU当前姿态相比于水平面的一个度量。
两种方法都是可行的,不过将重力方向单独表达出来会使得初始姿态表达更简单,还可以增加一些线性性。
如果把观测量和噪声量整理成一个向量,就可以把上式整理成矩阵形式。不过这样的矩阵形式将含有很多的零项,相比上式并不会有明显简化,所以先使用这种散开的公式。下面推导误差状态方程。
先定义误差状态变量为:
p
t
=
p
+
δ
p
v
t
=
v
+
δ
v
R
t
=
R
δ
R
或
q
t
=
q
δ
q
b
g
t
=
b
g
+
δ
b
g
b
a
t
=
b
a
+
δ
b
a
g
t
=
g
+
δ
g
\begin{matrix} p_{t} = p +\delta p \\ v_{t} = v +\delta v \\ R_{t} = R\delta R或q_{t}=q\delta q \\ b_{gt} = b_{g} +\delta b_{g} \\ b_{at} = b_{a} +\delta b_{a} \\ g_{t} = g +\delta g \end{matrix}
pt=p+δpvt=v+δvRt=RδR或qt=qδqbgt=bg+δbgbat=ba+δbagt=g+δg
不带下标的就是名义状态变量。名义状态变量的运动方程式与真值相同,只是不必考虑噪声(因为噪声在误差状态方程中考虑了)
其中旋转部分的
δ
R
\delta R
δR可以用它的李代数
E
x
p
(
δ
θ
)
Exp(\delta \theta )
Exp(δθ)表示,此时
R
t
=
R
δ
R
R_{t} = R\delta R
Rt=RδR需要改成用指数形式表示。
在误差状态的式中(除旋转外),在等式两侧分别对时间求导,得到对应的时间导数表达式:
δ
p
˙
=
δ
v
δ
b
g
˙
=
η
g
δ
b
a
˙
=
η
a
δ
g
˙
=
0
\begin{matrix} \delta \dot{p} =\delta v \\ \delta \dot{b_{g}} =\eta _{g} \\ \delta \dot{b_{a}} =\eta _{a} \\ \delta \dot{g} =0 \end{matrix}
δp˙=δvδbg˙=ηgδba˙=ηaδg˙=0
推导过程后面再补
经过一系列推导可以得到 误差变量的运动状态方程如下: