【🏠作者主页】：吴秋霖
【💼作者介绍】：擅长爬虫与JS加密逆向分析！Python领域优质创作者、CSDN博客专家、阿里云博客专家、华为云享专家。一路走来长期坚守并致力于Python与爬虫领域研究与开发工作！
【🌟作者推荐】：对爬虫领域以及JS逆向分析感兴趣的朋友可以关注《爬虫JS逆向实战》《深耕爬虫领域》
未来作者会持续更新所用到、学到、看到的技术知识！包括但不限于：各类验证码突防、爬虫APP与JS逆向分析、RPA自动化、分布式爬虫、Python领域等相关文章

作者声明：文章仅供学习交流与参考！严禁用于任何商业与非法用途！否则由此产生的一切后果均与作者无关！如有侵权，请联系作者本人进行删除！

1. 写在前面

  又到了周末学习技术的时间，最近准备购置一台设备，在让玩机变得更加伟大的同时想深度去研究学习一下APP逆向相关的东西。现在爬虫这个赛道在外面的市场已经可以说是非常卷了！多终端爬虫逆向能力已成为了大部分企业招聘的必备条件与要求

回想起七八年前刚入此道，哪有那么多逆向不逆向的。那个时候的爬虫是那么的纯粹而简单！自动化Boy那都是小公司的座上宾～

本期文章分析一下某毒的sign签名加密，它这个搜索跟详情的接口会比较复杂一些，请求参数跟响应数据都是加密的！

打开即巅峰，爬虫领域单拎一个方向出来都会发现是炸裂的！本身就是一个大杂烩领域，就下面这种各类验证码突防这块，都学不完～

2. 接口分析

打开网站地址，监测一下接口请求发包，可以看到sign参数加密，一般签名加密会采用MD5的加密方式，MD5常见的有16、32、40位！在之前的文章中有提到过在JS逆向中如何快速搜索定位加密函数。下面猜测是有MD5加密的，之后验证一下，如下所示：

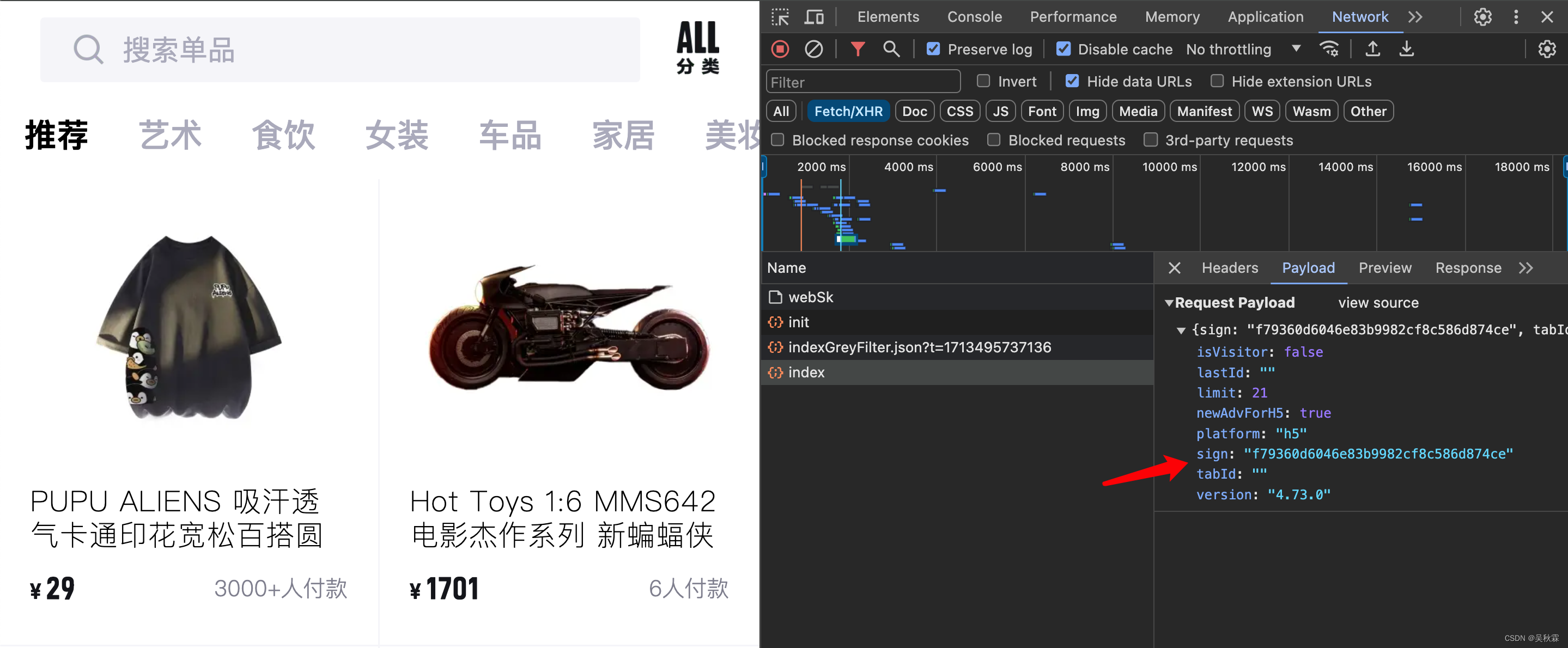
除了sign是动态的，其他的那些个参数都是一些固值

3. 断点分析

直接搜索是可以找到的，所以就不需要使用其他过于繁琐的定位方法与技巧。可以看到如下疑似sign参数生成的位置，如下所示：

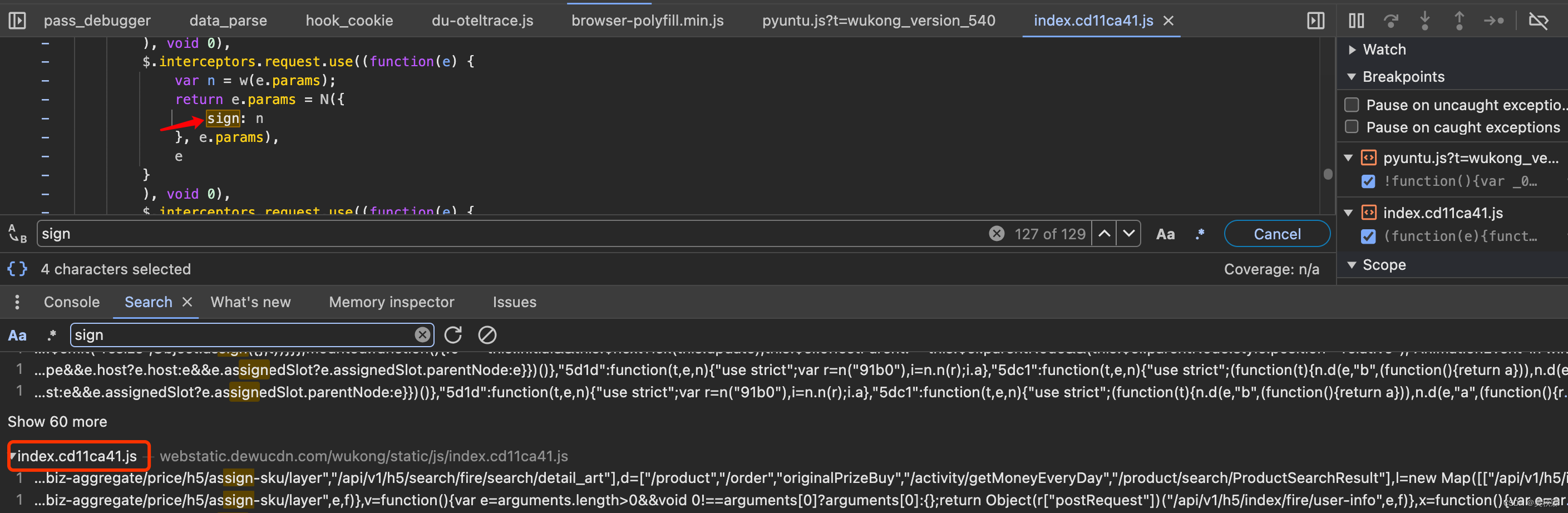
可以在这个地方下个断点，然后重新下拉加载一下页面触发断点，如下所示：

我们把上图部分的代码拿下来简单的看一下，n即加密参数，这里我们需要去分析的是w，它是加密方法，如下所示：

var n = w(e.params);
return e.params = N({
    sign: n
}, e.params)

直接跟到w方法内部看一下，单步进入来到下图位置处，这里直接跟到x[“e”]内，如下所示：

继续来到下图位置处，这里已经看到了之后需要开始扣代码的入口了，就是p，如下所示：

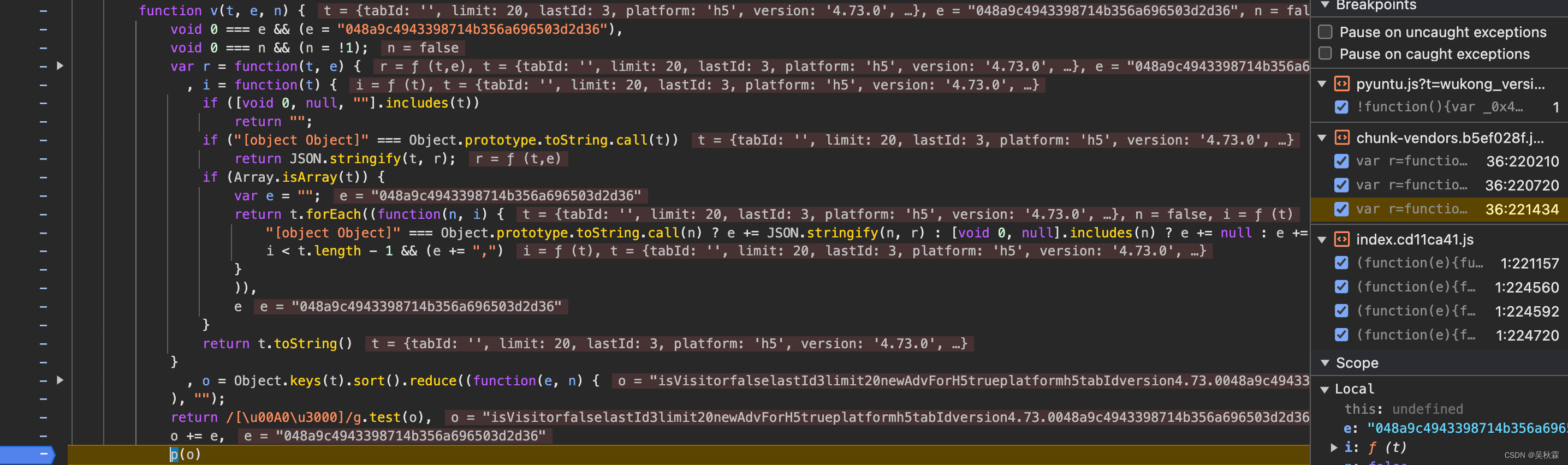
我们可以在控制台去查看验证一下，配合着断点，o是一串长字符，然后经过p生成最终的签名参数，如下所示：

上面p生成的签名参数与接口请求的是一致的，如下所示：

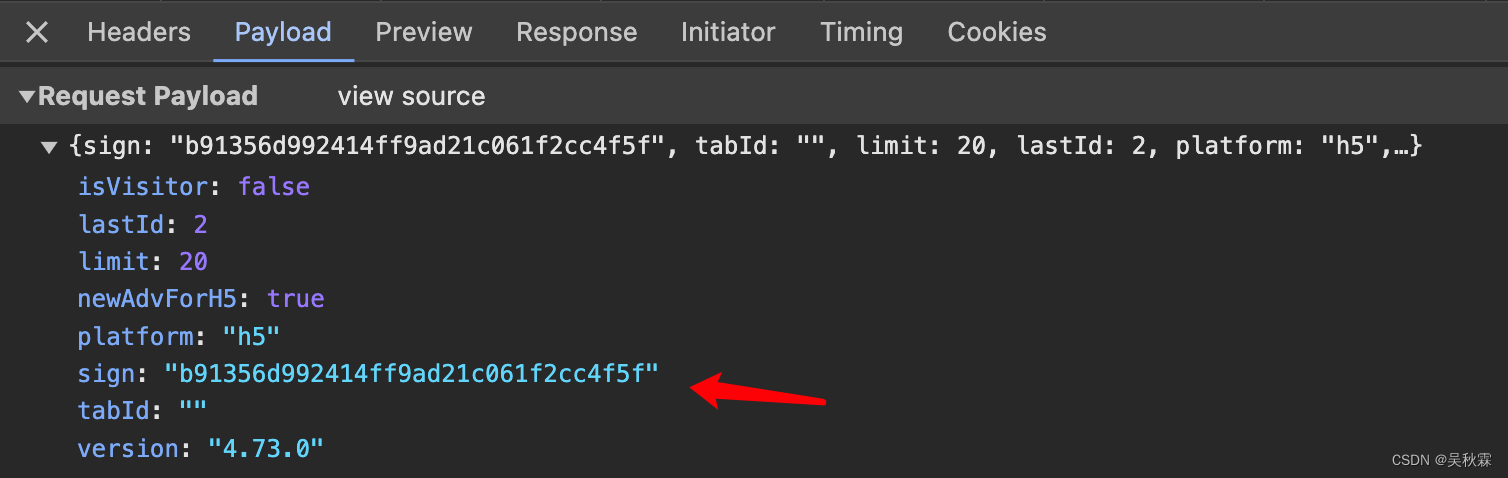
继续跟到p方法内，看下面代码特征会发现果真是MD5，这部分代码是一个完整的MD5算法实现，包含了一系列位操作和轮函数，如下所示：

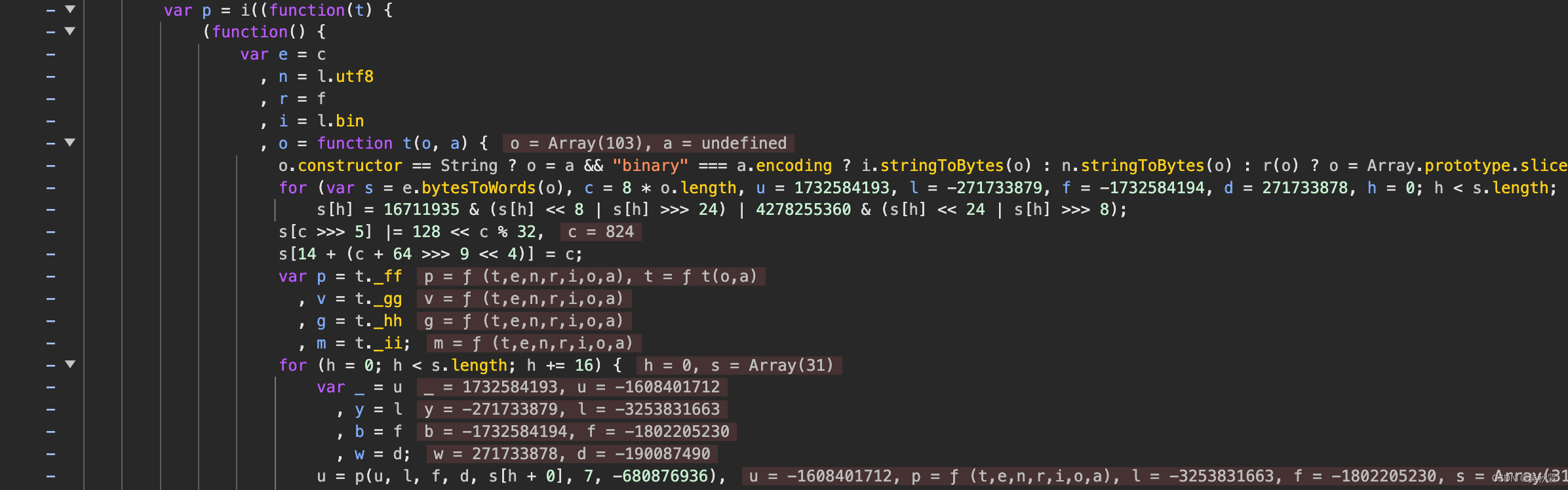
各种字符串转换字节数组，然后将字节数组转换成32位整数数组。然后初始化、填充、处理！最后将处理后的结果转换成字节数组，然后根据需要返回不同形式的结果，包括字节数组、字符串或十六进制字符串

整个算法串起来：对象转换字符串、进行MD5加密、将固值跟加密结果拼接，再返回最终结果

4. Python算法还原

按照上面梳理的流程直接扣JS算法即可，作者使用Py进行的算法还原！部分算法如下所示：

import json
import hashlib

def sign_hash(e):
    v = 7
    x = 12
    _ = 17
    w = 22
    C = 5
    S = 9
    T = 14
    P = 20
    E = 4
    I = 11
    A = 16
    k = 23
    O = 6
    B = 10
    D = 15
    L = 21
    e = y(e)
    b = f(e)
    c = 1732584193
    s = 4023233417
    m = 2562383102
    h = 271733878
    for n in range(0, len(b), 16):
        t = c
        i = s
        r = m
        a = h
        c = u(c, s, m, h, b[n + 0], v, 3614090360)
        h = u(h, c, s, m, b[n + 1], x, 3905402710)
        m = u(m, h, c, s, b[n + 2], _, 606105819)
        s = u(s, m, h, c, b[n + 3], w, 3250441966)
        c = u(c, s, m, h, b[n + 4], v, 4118548399)
        h = u(h, c, s, m, b[n + 5], x, 1200080426)
        m = u(m, h, c, s, b[n + 6], _, 2821735955)
        s = u(s, m, h, c, b[n + 7], w, 4249261313)
        c = u(c, s, m, h, b[n + 8], v, 1770035416)
        h = u(h, c, s, m, b[n + 9], x, 2336552879)
        m = u(m, h, c, s, b[n + 10], _, 4294925233)
        s = u(s, m, h, c, b[n + 11], w, 2304563134)
        c = u(c, s, m, h, b[n + 12], v, 1804603682)
        h = u(h, c, s, m, b[n + 13], x, 4254626195)
        m = u(m, h, c, s, b[n + 14], _, 2792965006)
        s = u(s, m, h, c, b[n + 15], w, 1236535329)
        c = d(c, s, m, h, b[n + 1], C, 4129170786)
        h = d(h, c, s, m, b[n + 6], S, 3225465664)
        m = d(m, h, c, s, b[n + 11], T, 643717713)
        s = d(s, m, h, c, b[n + 0], P, 3921069994)
        c = d(c, s, m, h, b[n + 5], C, 3593408605)
        h = d(h, c, s, m, b[n + 10], S, 38016083)
        m = d(m, h, c, s, b[n + 15], T, 3634488961)
        s = d(s, m, h, c, b[n + 4], P, 3889429448)
        c = d(c, s, m, h, b[n + 9], C, 568446438)
        h = d(h, c, s, m, b[n + 14], S, 3275163606)
        m = d(m, h, c, s, b[n + 3], T, 4107603335)
        s = d(s, m, h, c, b[n + 8], P, 1163531501)
        c = d(c, s, m, h, b[n + 13], C, 2850285829)
        h = d(h, c, s, m, b[n + 2], S, 4243563512)
        m = d(m, h, c, s, b[n + 7], T, 1735328473)
        s = d(s, m, h, c, b[n + 12], P, 2368359562)
        c = l(c, s, m, h, b[n + 5], E, 4294588738)
        h = l(h, c, s, m, b[n + 8], I, 2272392833)
        m = l(m, h, c, s, b[n + 11], A, 1839030562)
        s = l(s, m, h, c, b[n + 14], k, 4259657740)
        c = l(c, s, m, h, b[n + 1], E, 2763975236)
        h = l(h, c, s, m, b[n + 4], I, 1272893353)
        m = l(m, h, c, s, b[n + 7], A, 4139469664)
        s = l(s, m, h, c, b[n + 10], k, 3200236656)
        c = l(c, s, m, h, b[n + 13], E, 681279174)
        h = l(h, c, s, m, b[n + 0], I, 3936430074)
        m = l(m, h, c, s, b[n + 3], A, 3572445317)
        s = l(s, m, h, c, b[n + 6], k, 76029189)
        c = l(c, s, m, h, b[n + 9], E, 3654602809)
        h = l(h, c, s, m, b[n + 12], I, 3873151461)
        m = l(m, h, c, s, b[n + 15], A, 530742520)
        s = l(s, m, h, c, b[n + 2], k, 3299628645)
        c = p(c, s, m, h, b[n + 0], O, 4096336452)
        h = p(h, c, s, m, b[n + 7], B, 1126891415)
        m = p(m, h, c, s, b[n + 14], D, 2878612391)
        s = p(s, m, h, c, b[n + 5], L, 4237533241)
        c = p(c, s, m, h, b[n + 12], O, 1700485571)
        h = p(h, c, s, m, b[n + 3], B, 2399980690)
        m = p(m, h, c, s, b[n + 10], D, 4293915773)
        s = p(s, m, h, c, b[n + 1], L, 2240044497)
        c = p(c, s, m, h, b[n + 8], O, 1873313359)
        h = p(h, c, s, m, b[n + 15], B, 4264355552)
        m = p(m, h, c, s, b[n + 6], D, 2734768916)
        s = p(s, m, h, c, b[n + 13], L, 1309151649)
        c = p(c, s, m, h, b[n + 4], O, 4149444226)
        h = p(h, c, s, m, b[n + 11], B, 3174756917)
        m = p(m, h, c, s, b[n + 2], D, 718787259)
        s = p(s, m, h, c, b[n + 9], L, 3951481745)
        c = o(c, t)
        s = o(s, i)
        m = o(m, r)
        h = o(h, a)
    R = to_hex_string(c) + to_hex_string(s) + to_hex_string(m) + to_hex_string(h)
    return R.lower()

def to_hex_string(num):
    hex_string = ""
    for i in range(4):
        byte = num >> 8 * i & 255
        hex_byte = format(byte, 'x')
        hex_string += hex_byte.zfill(2)
    return hex_string

def generate_sign_string(params):
    to_str = lambda e: "" if e is None else ",".join(map(json.dumps, e)) if isinstance(e, list) else json.dumps(e) if isinstance(e, dict) else str(e)
    sorted_params = sorted([f"{k}{to_str(params[k])}" for k in params])
    sign_string = "".join(sorted_params) + "048a9c4943398714b356a696503d2d36"
    return sign_hash(sign_string)

需要完整算法学习，可找作者免费获取测试，未防止滥用文章今后不贴核心算法源码！！！

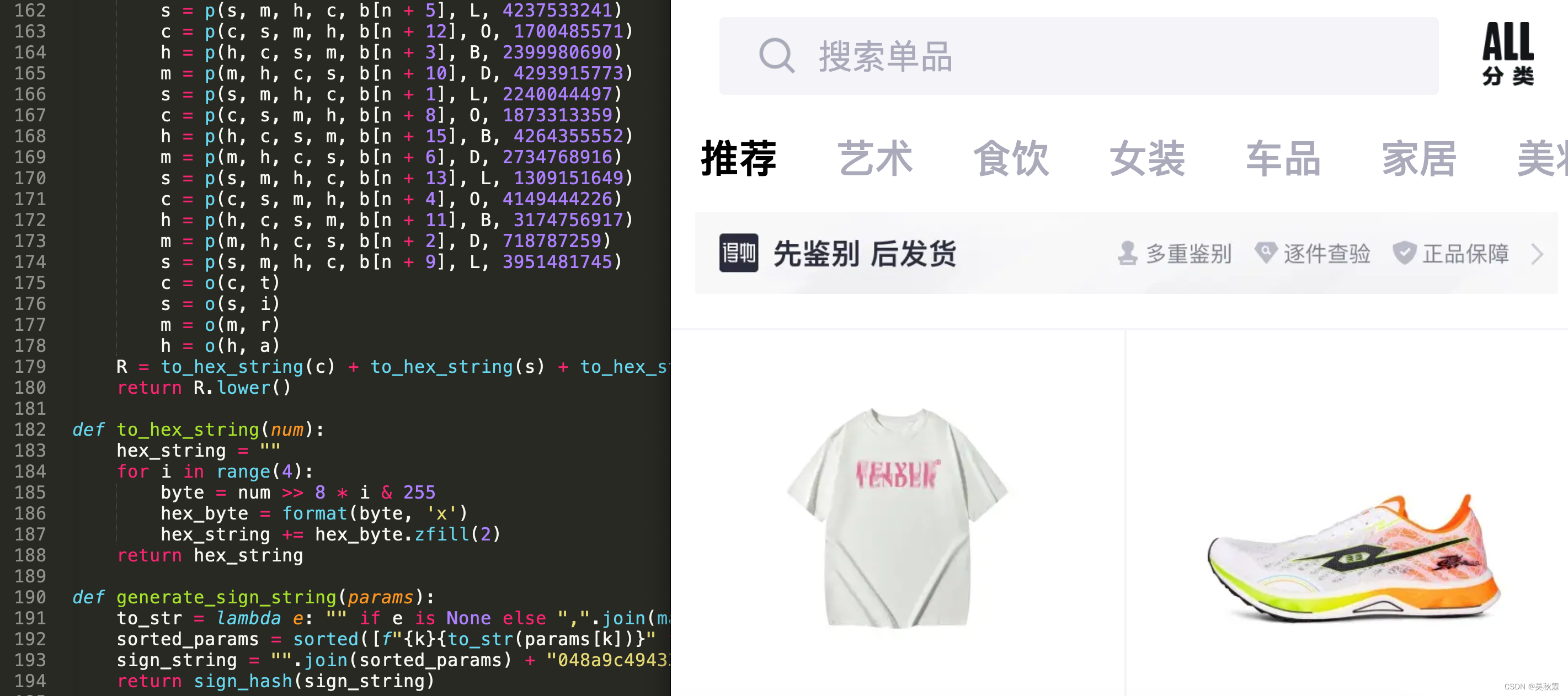
作者简单写了一个Python爬虫Demo调用上面的Py算法，进行了一下测试，效果如下所示：