文章目录
- 1. 前言 - 理解动态规划算法
- 1.5 关于dp路径问题
- 2. 例题
- 2.1_不同路径
- Warning. 关于状态表示
- 3. 算法题
- 3.1_不同路径II
- 3.2_珠宝的最高价值
- 3.3_下降路径最小和
- 3.4_最小路径和
- 3.5_地下城游戏
- 关于状态表示的两种选法:
1. 前言 - 理解动态规划算法
关于 动态规划的理解 与例题,点击👇
【动态规划】C++解决斐波那契模型题目(三步问题、爬楼梯、解码方法…)
有了上面的经验,我们来解下面 dp的路径问题 :
1.5 关于dp路径问题
-
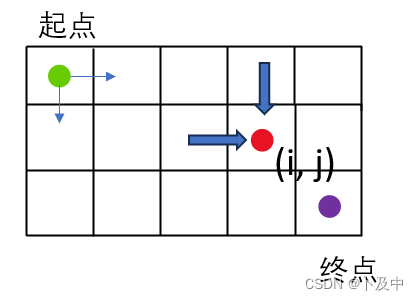
在路径问题中,通常需要找到从起点到终点的一条路径,使得路径满足一定的约束条件(如最短路径、最大价值路径等)。
-
在动态规划中,通常采用一个二维数组或类似的数据结构来存储中间状态,其中每个状态表示从起点到当前位置的某种信息(如路径长度、路径价值等)。
2. 例题
2.1_不同路径

思路
- 首先 找状态表示 与 状态转移方程
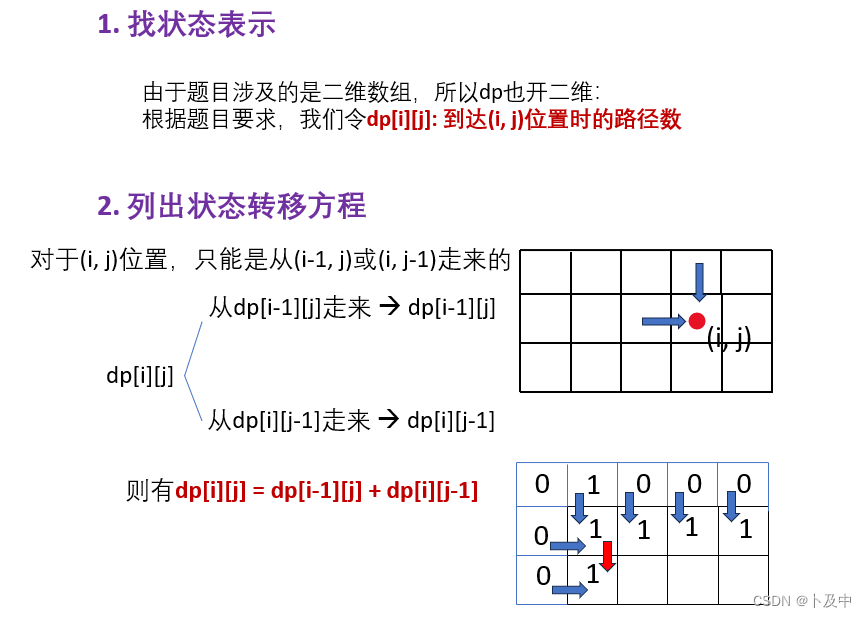
Warning. 关于状态表示
实际上在分析状态表示 时,一般会考虑两种表示法:
- 以(i, j)位置为终点 时的count
- 以(i, j)位置为起点 到终点时的count
在本章算法题中,仅最后一道题会涉及到两种表示法,其余的题以第一种即可解题。
- 随后进行 对表中内容的初始化 (以及细节问题:填表顺序、返回值)
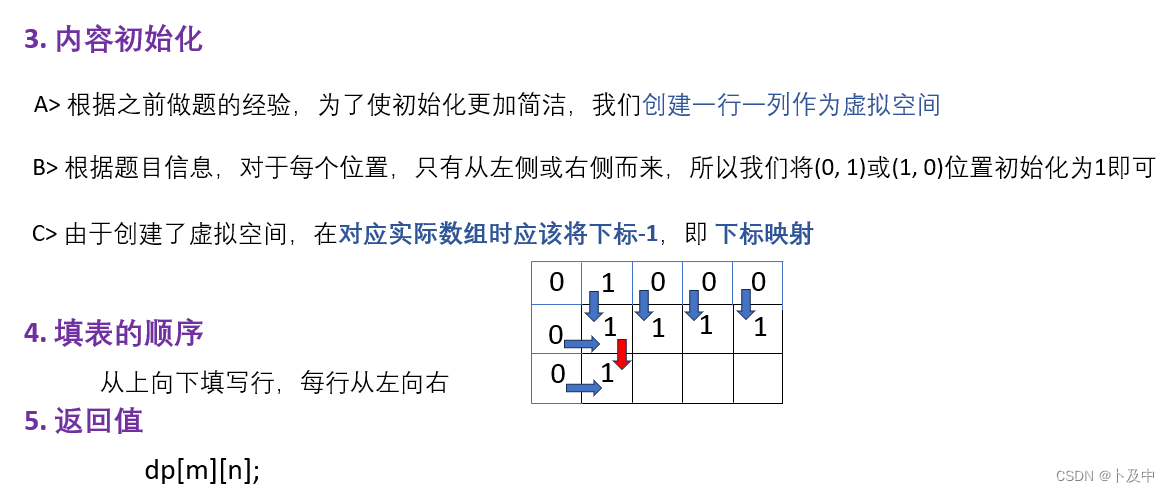
代码
class Solution {
public:
int uniquePaths(int m, int n) {
// 创建dp表
vector<vector<int>> dp(m + 1, vector<int>(n + 1)); // 虚拟空间
// 填写虚拟空间(默认为0!!)
// for(int i = 0; i <= m; ++i) dp[0][i] = 0;
// for(int j = 0; j <= n; ++j) dp[j][0] = 0;
dp[0][1] = 1;
// 编写状态转移方程
for(int i = 1; i <= m; ++i)
for(int j = 1; j <= n; ++j)
{
dp[i][j] = dp[i-1][j] + dp[i][j-1];
}
return dp[m][n];
}
};
3. 算法题
3.1_不同路径II
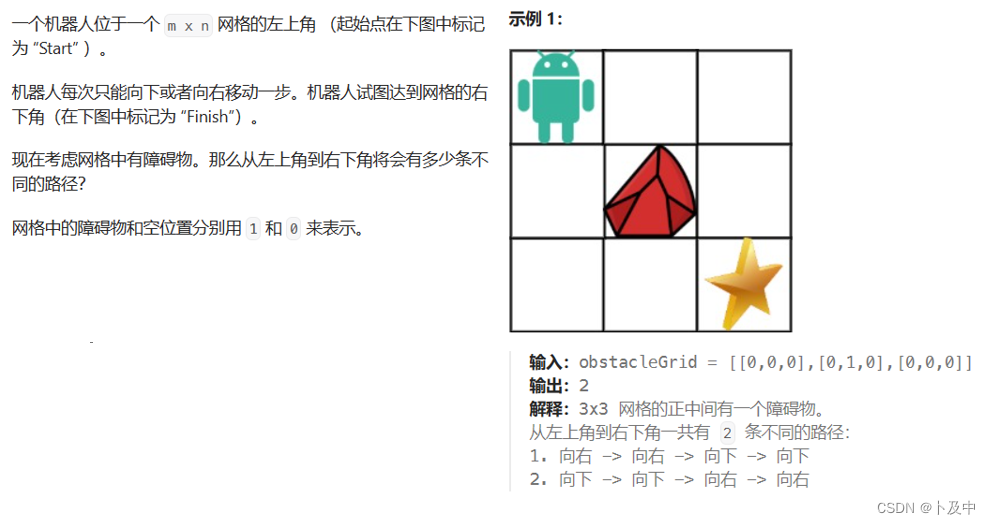
思路
读题后,我们发现本题比起之前的,仅仅加了障碍物的限制。
- 所以我们只需要在填表时加一句判断即可,当(i, j)位置不为障碍物时,进行填表dp[i][j]。
- 为什么?
- 当(i, j)为障碍物,dp[i][j]为0,不做统计。
- 为什么?
代码
class Solution {
public:
int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
int m = obstacleGrid.size(), n = obstacleGrid[0].size();
vector<vector<int>> dp(m + 1, vector<int>(n + 1)); // 初始化dp数组(虚拟空间+1行1列)
dp[0][1] = 1;
for(int i = 1; i <= m; ++i)
for(int j = 1; j <= n; ++j)
{
if(obstacleGrid[i - 1][j - 1] == 0) // 虚拟空间多加了一行一列,找初始矩阵时,映射下标要-1
dp[i][j] = dp[i-1][j] + dp[i][j-1];
}
return dp[m][n];
}
};
3.2_珠宝的最高价值

思路
- 首先 找状态表示 与 状态转移方程
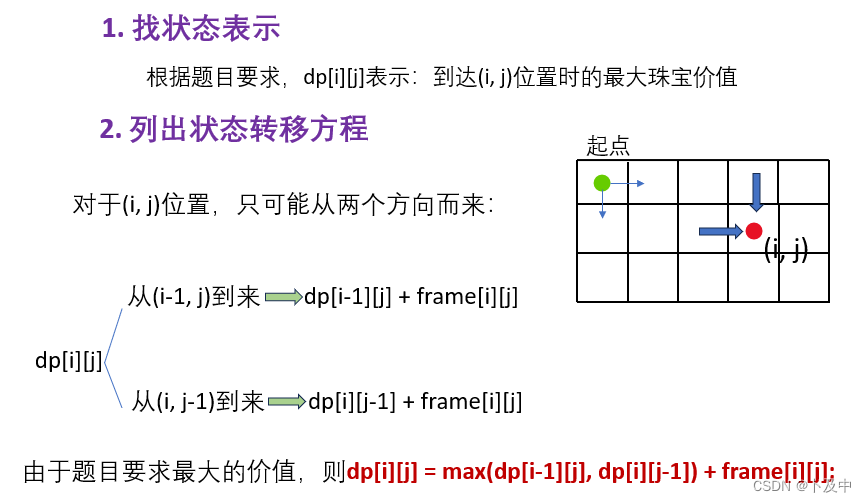
- 随后进行 对表中内容的初始化 (以及细节问题:填表顺序、返回值)
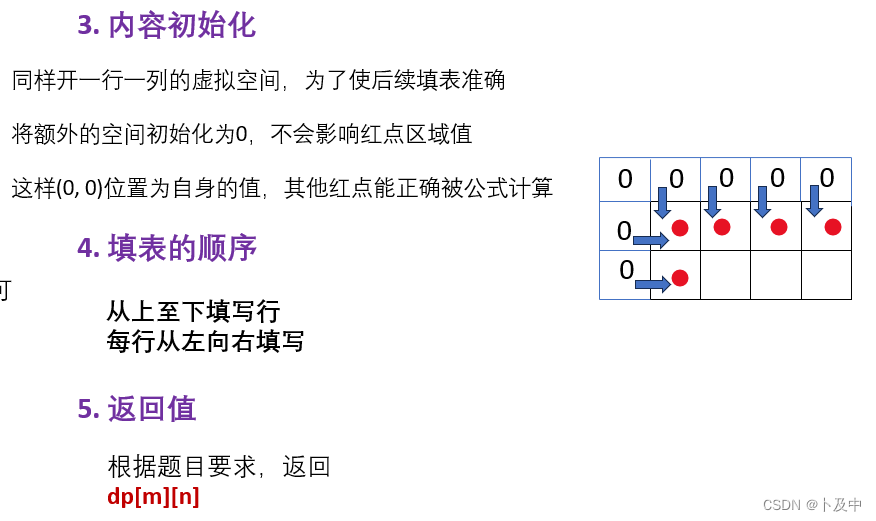
代码
class Solution {
public:
int jewelleryValue(vector<vector<int>>& frame) {
int m = frame.size(), n = frame[0].size();
// dp的创建 与 元素初始化
vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));
for(int i = 1; i <= m; ++i)
for(int j = 1; j <= n; ++j)
dp[i][j] = max(dp[i-1][j], dp[i][j-1]) + frame[i-1][j-1]; // 映射下标(对于frame要-1)
return dp[m][n];
}
};
3.3_下降路径最小和
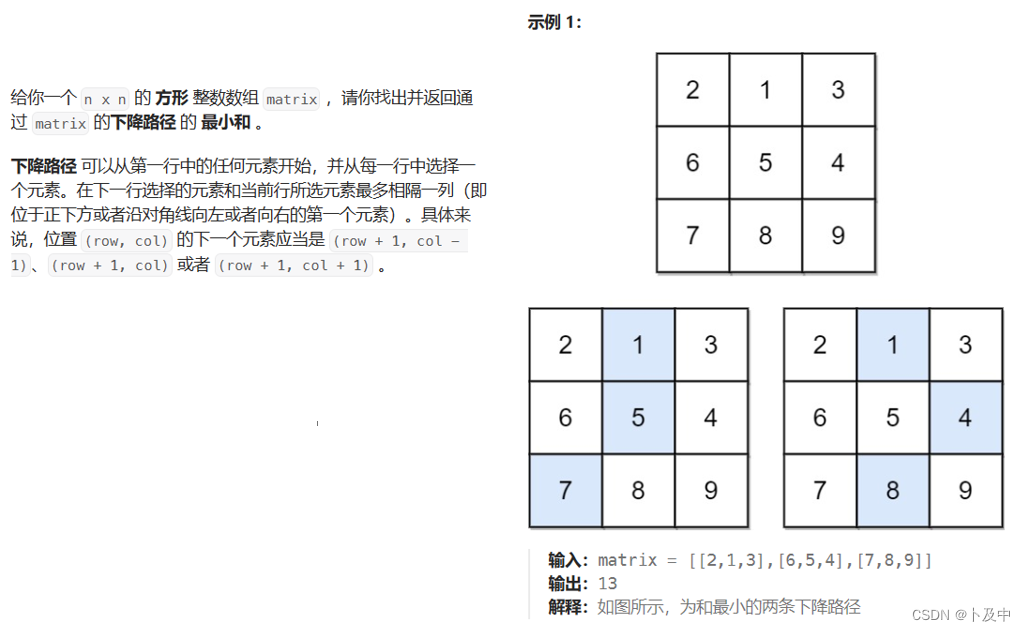
思路
不再过多解释,直接跟着思路五步走:
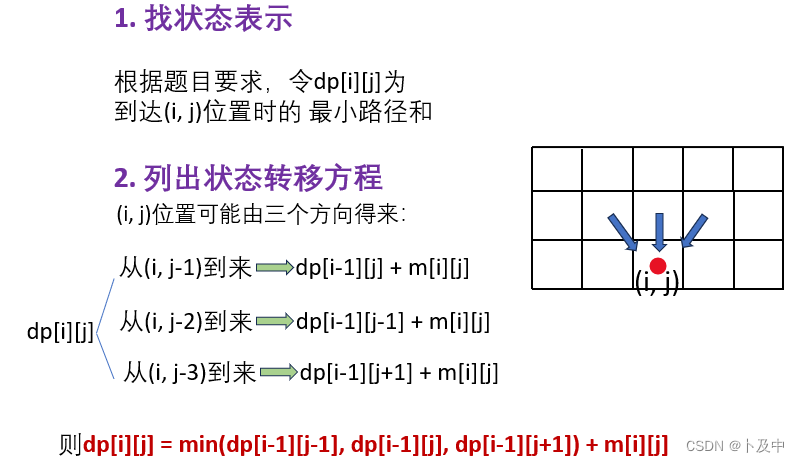
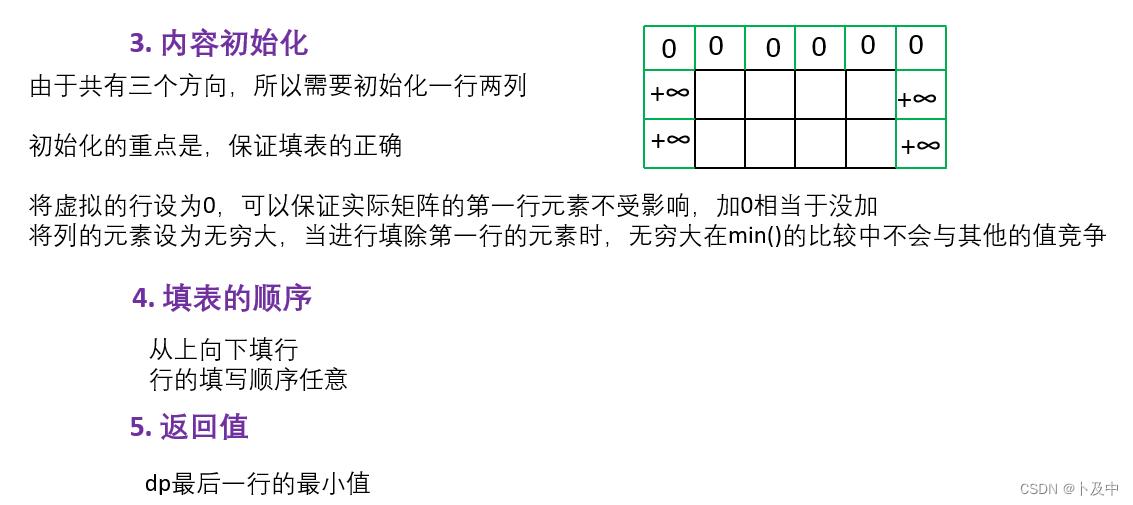
代码
class Solution {
public:
int minFallingPathSum(vector<vector<int>>& matrix) {
int n = matrix.size();
vector<vector<int>> dp(n + 1, vector<int>(n + 2, INT_MAX)); // 先初始化为 大值
for(int j = 0; j <= n + 1; ++j) dp[0][j] = 0; // 将第一行初始化为0
for(int i = 1; i <= n; ++i)
for(int j = 1; j <= n; ++j)
{
// 映射下标,matrix下标-1
dp[i][j] = min(min(dp[i-1][j], dp[i-1][j-1]), dp[i-1][j+1]) + matrix[i-1][j-1];
}
// 找最后一行的最小值
int ret = INT_MAX;
for(int j = 1; j <= n; ++j) ret = min(ret, dp[n][j]);
return ret;
}
};
3.4_最小路径和
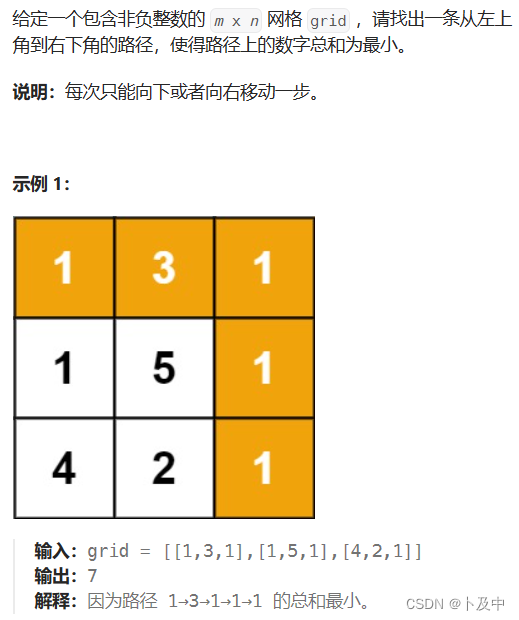
思路
- 题目分析:本题不再画图,根据题目可以看出来和《珠宝的最高价值》一题是极为相似的,需要注意的是初始化时虚拟空间值的设置。
代码
class Solution {
public:
int minPathSum(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size();
vector<vector<int>> dp(m + 1, vector<int>(n + 1, INT_MAX)); // 虚拟空间+1行1列。初始化为无穷大
dp[0][1] = dp[1][0] = 0;
for(int i = 1; i <= m; ++i)
for(int j = 1; j <= n; ++j)
dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i-1][j-1]; // grid 映射下标(需要-1)
return dp[m][n];
}
};
3.5_地下城游戏
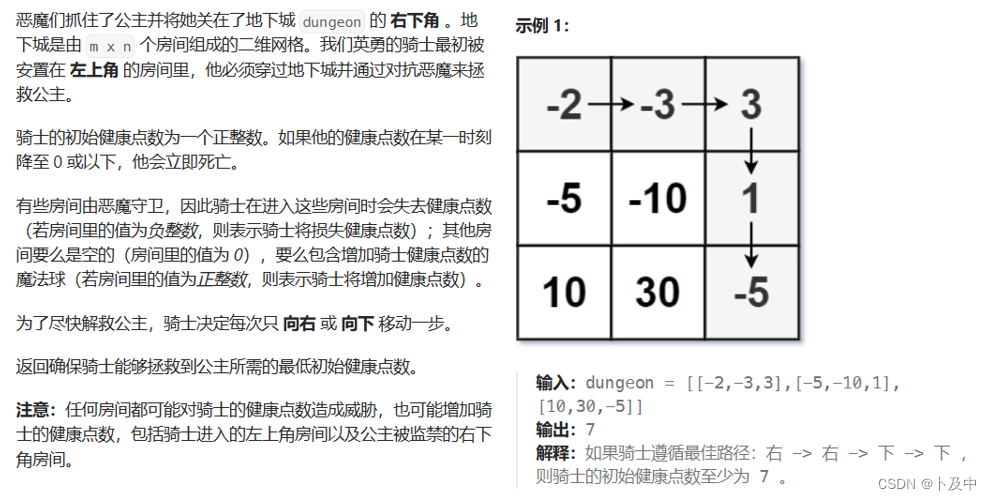
思路
关于状态表示的两种选法:
下面介绍了,为什么对于本题我们无法继续以(i, j)位置为终点,找健康点数
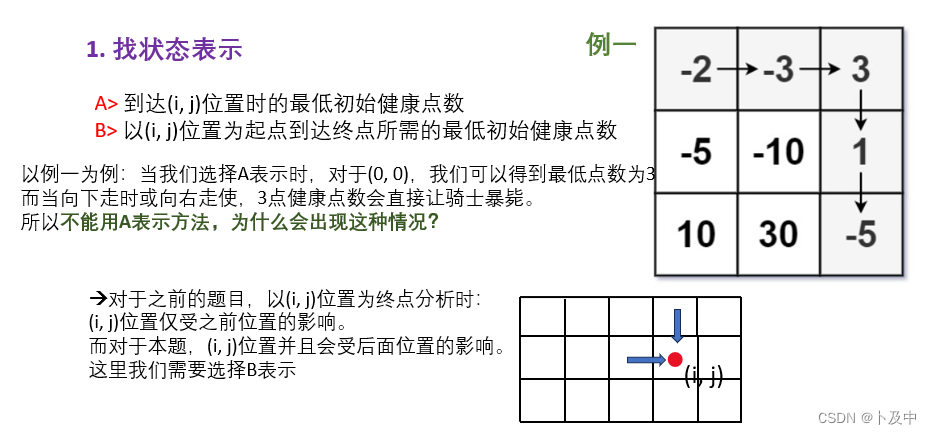
设置了正确的状态表示才能写出正确的状态转移方程:
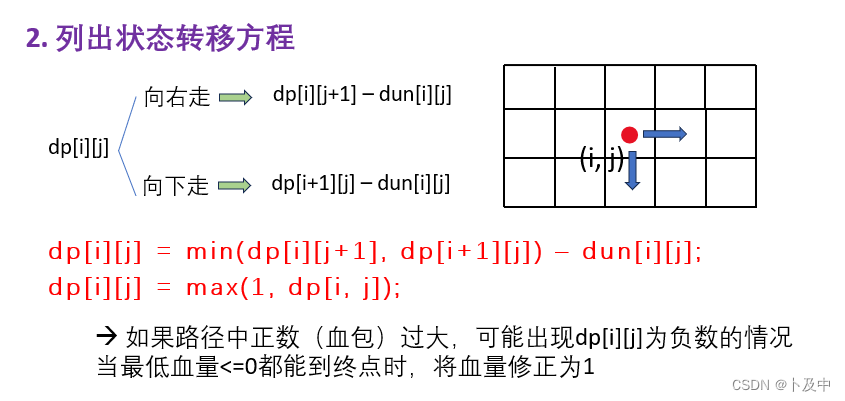
最后进行内容初始化以及其余细节问题:
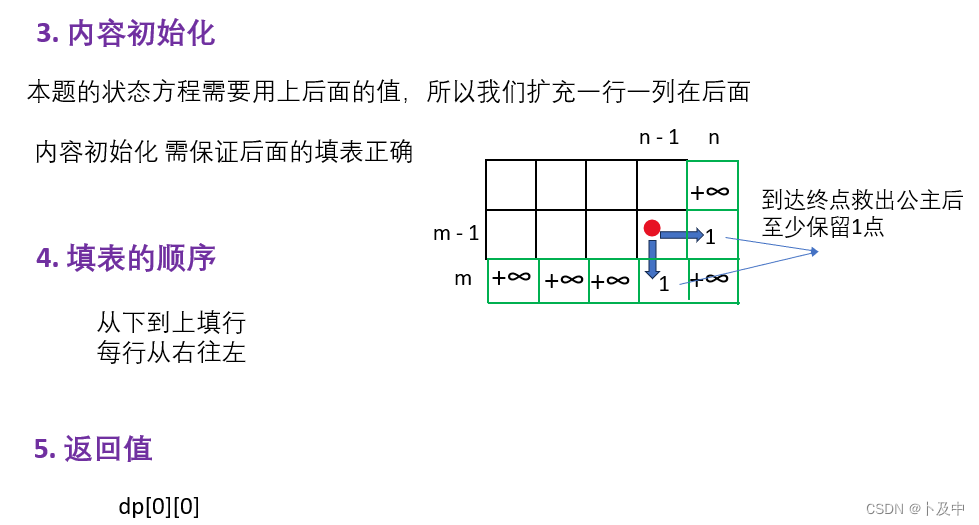
代码
class Solution {
public:
int calculateMinimumHP(vector<vector<int>>& dungeon) {
int m = dungeon.size(), n = dungeon[0].size();
// dp[i][j]: 以(i, j)位置开始,到达终点的 最低初始健康点数
// 右侧下侧扩充一行一列
vector<vector<int>> dp(m + 1, vector<int>(n + 1, INT_MAX));
dp[m-1][n] = dp[m][n-1] = 1; // 初始化
for(int i = m - 1; i >= 0; --i)
for(int j = n - 1; j >= 0; --j)
{
dp[i][j] = min(dp[i+1][j], dp[i][j+1]) - dungeon[i][j];
dp[i][j] = max(1, dp[i][j]); // 防止负数血量的出现
}
return dp[0][0];
}
};