前言
今天来讲一讲高精度算法,我们说一个数据类型,有它的对应范围比如int类型最多
可以包含到负2的31次方到2的31次方减一
其实大概就是20亿左右那么其他的类型也同样如此
那么,如何解决一个很大很大的数的运算呢?
我们今天介绍两种对于整数的高精度加法和高精度除法
还算是比较简单的算法,但实现起来仍然有细节
高精度加法
对于两个很大很大的数,我们已经无法用任何整型来记录它更不能对其运算,那么此时我们完全可以使用字符串来记录要进行加法的数
我们以题目为例
输入两个数 a b 0<a< 0<b<
,求两个数之和,这里的数为整数
思路
使用字符串记录两个数,当然这个字符串的大小范围取决于数的范围最多有500位数
(不包括) 那么字符数组大小只要大于500就可以了
把它用字符数组记住后该数的高位对应字符数组低下标
所以我们需要逆转这个字符数组,并让它储存在整型数组中,最后让这个个数所对应的
相加,满10进1,就完成了.
当然这两个操作数都是正数,那如果有负数,怎么办那么我们可以把它当成减法嘛
思路是如此实现起来还有很多细节,会在代码中注释出来的,好好看,可以看懂的
看代码吧
//高精度算法
char a[505];
char b[505];
int a1[505];
int b1[505];
int result[505];
int main()
{
printf("请输入两个数\n");
scanf("%s", a);
scanf("%s", b);
int lc, la, lb;
la = strlen(a);
lb = strlen(b);
//遇10进1,有可能位数是a b 中最大的或者是最大的加上1
//所以在这里默认使位数加一,后面可以判断是否有改位
lc = la > lb ? la + 1 : lb + 1;
//逆置字符串,方便运算,毕竟要从低位开始算,
//把低位放在低下标处
for (int i = 0; i <la; i++)
{
a1[la-i-1] = a[i] - '0';
}
for (int i = 0; i < lb; i++)
{
b1[lb-i-1] = b[i] - '0';
}
for (int i = 0; i < lc; i++)
{
result[i]+=a1[i] + b1[i];
result[i + 1] += result[i]/10;
result[i]%=10;
}
//但是这里值的注意的是
//对于加法最多会多一个前置0
//判断并清除前置0
if(result[lc]==0)lc--;
for (int i = lc - 1; i >= 0; i--)
{
printf("%d", result[i]);
}
return 0;
}一些细节全部都在代码的注释上了
当然 我们其实完全可以不构建太多变量,来实现优化
说一说思路,但是这个代码写起来就会变得难理解了
我们完全可以只构建两个char arr[] char brr[] 数组
然后直接把他们逆置,通过brr[]字符数组先可以去一个字符0在加到字符arr[]中如果大于字符‘9’+1
所对应的Ascll值就可以让和减去数字10,让下一位加数字1这样也可以解决问题
最后通过判断长度以及清除前置的‘0’来输出结果
不过没有太大必要 代码都差不多,就这么点空间,其实区别不大
好吧!我们看看测试的结果
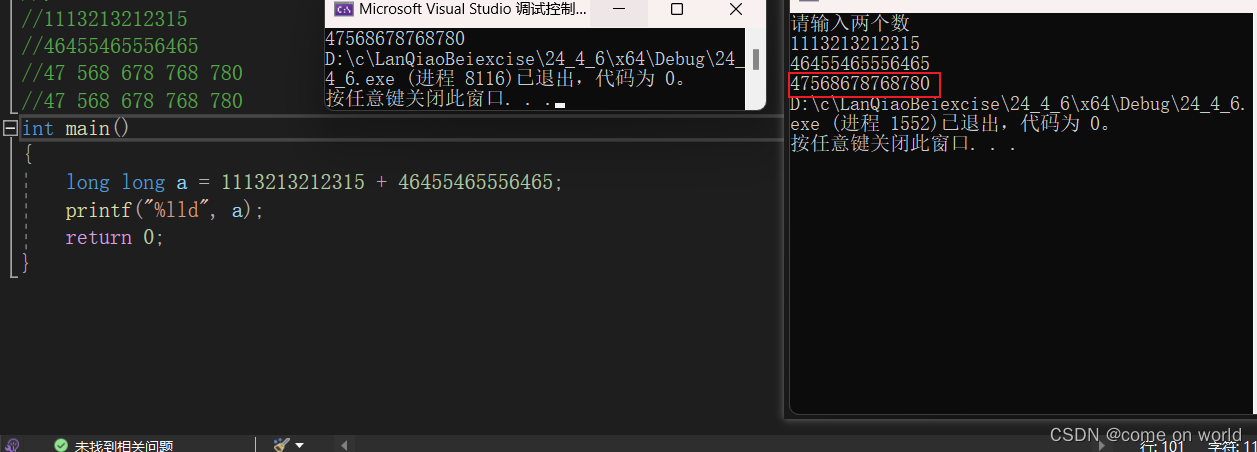
左边是测试值右边是执行代码的结果 两者一样 nice!那么该程序就是可以计算更高精度的整数
高精度减法
高精度减法的思路与加法差不多
但是要多出一个判断,我们就用大或等的数减去小的数,得到一个非负数,最后再判断是否要添加负号
核心思路就是低位减去低位,若大数的低位小于小数的低位,那么低位向高位借一位
看个例题
计算最大10000位的正数之间的减法
多说无益 代码走起
//高精度减法
char s1[10090];
char s2[10090];
char s3[10090];
int a[10090];
int b[10090];
int c[10090];
bool flag;
bool cmpare(char *p1,char* p2)
{
int lp1= strlen(p1);
int lp2 = strlen(p2);
if (lp1 > lp2)
return true;
else if (lp1 == lp2)
{
if (strcmp(p1, p2) >= 0)
return true;
else
return false;
}
else
return false;
}
int main()
{
while (1)
{
printf("请输入被减数与减数\n");
scanf("%s", s1);
scanf("%s", s2);
if (!cmpare(s1, s2))
{
flag = true;
strcpy(s3, s1);
strcpy(s1, s2);
strcpy(s2, s3);
}
int la = strlen(s1);
int lb = strlen(s2);
int lc = la > lb ? la : lb;
//逆置字符数组
for (int i = 0; i < la; i++)
{
a[la - i] = s1[i] - '0';
}
for (int i = 0; i < lb; i++)
{
b[lb - i] = s2[i] - '0';
}
for (int i = 1; i <= lc; i++)
{
if (a[i] < b[i])
{
a[i + 1]--;
a[i] += 10;
}
c[i] = a[i] - b[i];
}
//清除前置0,如果两个数相等,我们就要清除位数-1个0
//举例100-100=000 我们要清除这两个三位数的两个0
//这里要用循环来解决
while (c[lc] == 0 && lc > 1)lc--;
//判断正负
if (flag)
{
printf("-");
flag = false;
}
for (int i = lc; i >0; i--)
printf("%d", c[i]);
printf("\n");
}
return 0;
}看看代码吧
细节还是很多的,值得注意的·
1就是那么前置0的清除
2还有就是a b整型数组是从1开始的
3ic的大小至少为1
还是那样,今天就这样了,继续努力