作者主页: 🔗进朱者赤的博客
精选专栏:🔗经典算法
作者简介:阿里非典型程序员一枚 ,记录在大厂的打怪升级之路。 一起学习Java、大数据、数据结构算法(公众号同名)
❤️觉得文章还不错的话欢迎大家点赞👍➕收藏⭐️➕评论,💬支持博主,记得点个大大的
关注,持续更新🤞
————————————————-
文章目录
- 题目描述
- 思路及实现
- 方式一:动态规划(朴素DP )
- 思路
- 代码实现
- Java版本
- C语言版本
- Python3版本
- go
- 复杂度分析
- 方式二:滚动数组优化DP
- 思路
- 代码实现
- Java版本
- C语言版本
- Python3版本
- go
- 复杂度分析
- 总结
- 相似题目
- 标签(题目类型):动态规划
题目描述
给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,
使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步。
示例 1:
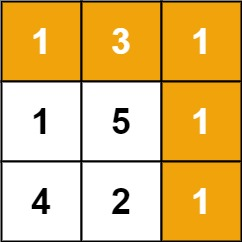
输入:grid = [[1,3,1],[1,5,1],[4,2,1]]
输出:7
解释:因为路径 1→3→1→1→1 的总和最小。
示例 2:
输入:grid = [[1,2,3],[4,5,6]]
输出:12
提示:
m == grid.length
n == grid[i].length
1 <= m, n <= 200
0 <= grid[i][j] <= 200
原题:LeetCode 64.最小路径和
思路及实现
方式一:动态规划(朴素DP )
思路
可以使用动态规划来求解最小路径和。
要求从左上角转移到右下角的最小路径和,每次只能往右走或者往下走。换句话说,对于位置 (i, j),其只能从 (i-1, j) 和 (i, j-1) 两个位置转移而来。我们设 dp[i][j] 表示到达位置 (i, j) 的最小路径和。
那么 dp[i][j] 肯定要从 dp[i-1][j] 和 dp[i][j-1] 中那个更小的状态转移过来,
因此状态转移方程为:dp[i][j] = min(dp[i][j-1], dp[i-1][j]) + grid[i][j]。
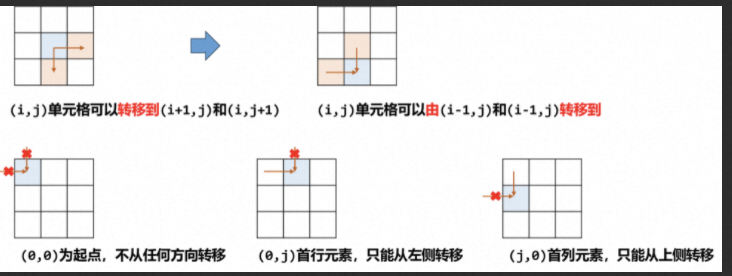
边界条件:
- 当 i = 0, j = 0 时,即左上角位置,其左侧和上侧单元格都不存在,
dp[0][0] = grid[0][0]; - 当 i = 0, j ≠ 0 时,即首行元素,其上侧单元格不存在,
dp[0][j] = dp[0][j-1] + grid[0][j]; - 当 i ≠ 0, j = 0 时,即首列元素,其左侧单元格不存在,
dp[i][0] = dp[i-1][0] + grid[i][0];
代码实现
Java版本
public class Solution {
public int minPathSum(int[][] grid) {
if (grid == null || grid.length == 0 || grid[0].length == 0) {
return 0;
}
int m = grid.length;
int n = grid[0].length;
int[][] dp = new int[m][n];
// 初始化第一行和第一列
//初始化第一个元素
dp[0][0] = grid[0][0];
// 初始化第一行
for (int i = 1; i < m; i++) {
dp[i][0] = dp[i - 1][0] + grid[i][0];
}
// 初始化第一列
for (int j = 1; j < n; j++) {
dp[0][j] = dp[0][j - 1] + grid[0][j];
}
// 填充其他位置
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
}
}
// 最后一个元素即结果
return dp[m - 1][n - 1];
}
}
说明:
此解法使用动态规划,时间复杂度为 O(mn),空间复杂度也为 O(mn)。
C语言版本
#include <stdio.h>
#include <limits.h>
int minPathSum(int** grid, int gridSize, int* gridColSize){
if (grid == NULL || gridSize == 0 || gridColSize[0] == 0) {
return 0;
}
int m = gridSize;
int n = gridColSize[0];
int** dp = (int**)malloc(m * sizeof(int*));
for (int i = 0; i < m; i++) {
dp[i] = (int*)malloc(n * sizeof(int));
}
// 初始化第一行和第一列
dp[0][0] = grid[0][0];
for (int i = 1; i < m; i++) {
dp[i][0] = dp[i - 1][0] + grid[i][0];
}
for (int j = 1; j < n; j++) {
dp[0][j] = dp[0][j - 1] + grid[0][j];
}
// 填充其他位置
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = (dp[i - 1][j] < dp[i][j - 1]) ? (dp[i - 1][j] + grid[i][j]) : (dp[i][j - 1] + grid[i][j]);
}
}
int result = dp[m - 1][n - 1];
// 释放动态分配的内存
for (int i = 00; i < m; i++) {
free(dp[i]);
}
free(dp);
return result;
}
int main() {
// 示例网格
int gridSize = 3;
int gridColSize[3] = {3, 3, 3};
int grid[3][3] = {{1, 3, 1}, {1, 5, 1}, {4, 2, 1}};
int** gridPtr = (int**)malloc(gridSize * sizeof(int*));
for (int i = 0; i < gridSize; i++) {
gridPtr[i] = grid[i];
}
int minSum = minPathSum(gridPtr, gridSize, gridColSize);
printf("The minimum path sum is: %d\n", minSum);
// 释放动态分配的内存
free(gridPtr);
return 0;
}
说明:
C语言版本同样使用动态规划,时间复杂度和空间复杂度与Java版本相同。注意在C语言中需要手动管理内存,因此在函数结束时需要释放动态分配的内存。
Python3版本
def minPathSum(grid):
if not grid or not grid[0]:
return 0
m, n = len(grid), len(grid[0])
dp = [[0] * n for _ in range(m)]
# 初始化第一行和第一列
dp[0][0] = grid[0][0]
for i in range(1, m):
dp[i][0] = dp[i - 1][0] + grid[i][0]
for j in range(1, n):
dp[0][j] = dp[0][j - 1] + grid[0][j]
# 填充其他位置
for i in range(1, m):
for j in range(1, n):
dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j]
return dp[m - 1][n - 1]
# test
# 示例网格
grid = [
[1, 3, 1],
[1, 5, 1],
[4, 2, 1]
]
min_sum = minPathSum(grid)
print(f"The minimum path sum is: {min_sum}")
说明:
Python3版本使用动态规划,简洁易懂。由于Python中的列表支持动态大小,因此不需要手动管理内存。
go
// minPathSum 使用朴素DP方法求解最小路径和
func minPathSum(grid [][]int) int {
if len(grid) == 0 || len(grid[0]) == 0 {
return 0
}
rows, cols := len(grid), len(grid[0])
// 创建一个二维DP数组,大小与grid相同,用于存储到达每个位置的最小路径和
dp := make([][]int, rows)
for i := range dp {
dp[i] = make([]int, cols)
}
// 初始化第一行和第一列
dp[0][0] = grid[0][0]
for i := 1; i < rows; i++ {
dp[i][0] = dp[i-1][0] + grid[i][0] // 第一列的最小路径和依赖于上一行的值
}
for j := 1; j < cols; j++ {
dp[0][j] = dp[0][j-1] + grid[0][j] // 第一行的最小路径和依赖于前一列的值
}
// 填充剩余的DP数组
for i := 1; i < rows; i++ {
for j := 1; j < cols; j++ {
// 当前位置的最小路径和取上方和左方位置的最小路径和加上当前位置的值
dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j]
}
}
// 返回右下角位置的最小路径和
return dp[rows-1][cols-1]
}
// min 返回两个整数中的较小值
func min(a, b int) int {
if a < b {
return a
}
return b
}
// 示例使用
func main() {
grid := [][]int{
{1, 3, 1},
{1, 5, 1},
{4, 2, 1},
}
minSum := minPathSum(grid)
fmt.Printf("The minimum path sum is: %d\n", minSum)
}
说明:
minPathSum:使用朴素DP算法计算从grid左上角到右下角的最小路径和。
逻辑步骤
- 初始化二维DP数组
dp,大小与grid相同。- 填充
dp数组的第一行和第一列。- 遍历
grid剩余元素,根据状态转移方程填充dp数组。- 返回
dp数组的右下角元素作为结果。
复杂度分析
- 时间复杂度:O(mn),其中 m 和 n 分别是网格的行数和列数。需要遍历每个网格位置一次。
- 空间复杂度:O(mn),需要一个二维数组 dp 来存储每个位置的最小路径和。
方式二:滚动数组优化DP
对于上述的动态规划解法,我们注意到在计算 dp[i][j] 时,只依赖于其正上方和左方的值。因此,我们可以使用滚动数组来优化空间复杂度,将空间复杂度从 O(mn) 降低到 O(n)。
思路
由于每一行的计算只依赖于上一行的值,我们可以只保留上一行的值,并在当前行上直接计算。这样,我们只需要一个一维数组来存储上一行的值即可。
代码实现
Java版本
public int minPathSum(int[][] grid) {
if (grid == null || grid.length == 0 || grid[0].length == 0) {
return 0;
}
int m = grid.length;
int n = grid[0].length;
int[] dp = new int[n];
// 初始化第一行
dp[0] = grid[0][0];
for (int j = 1; j < n; j++) {
dp[j] = dp[j - 1] + grid[0][j];
}
// 填充其他行
for (int i = 1; i < m; i++) {
int prev = dp[0]; // 保存上一行的第一个值,因为下一个dp[0]会被覆盖
for (int j = 0; j < n; j++) {
int curr = dp[j]; // 保存当前位置的值,因为下一个dp[j]会被覆盖
if (j == 0) {
// 如果是第一列,则只能从上方来
dp[j] = prev + grid[i][j];
} else {
// 否则取上方和左方的最小值
dp[j] = Math.min(prev, dp[j]) + grid[i][j];
}
prev = curr; // 更新prev为下一个位置的上一行值
}
}
// dp数组的最后一个元素即为最小路径和
return dp[n - 1];
}
C语言版本
#include <stdio.h>
#include <stdlib.h>
#include <limits.h>
int minPathSum(int** grid, int gridSize, int* gridColSize) {
if (grid == NULL || gridSize == 0 || gridColSize[0] == 0) {
return 0;
}
int n = gridColSize[0];
int* dp = (int*)malloc(n * sizeof(int));
if (dp == NULL) {
return -1;
}
// 初始化第一行
dp[0] = grid[0][0];
for (int j = 1; j < n; j++) {
dp[j] = dp[j - 1] + grid[0][j];
}
// 填充其他行
for (int i = 1; i < gridSize; i++) {
int prev = dp[0]; // 保存上一行的第一个值
for (int j = 0; j < n; j++) {
int temp = dp[j]; // 临时保存当前位置的值
if (j == 0) {
dp[j] = prev + grid[i][j];
} else {
dp[j] = (prev < dp[j]) ? (prev + grid[i][j]) : (dp[j] + grid[i][j]);
}
prev = temp; // 更新prev
}
}
int result = dp[n - 1];
free(dp);
return result;
}
int main() {
int gridSize = 3;
int gridColSize[3] = {3, 3, 3};
int grid[3][3] = {{1, 3, 1}, {1, 5, 1}, {4, 2, 1}};
int** gridPtr = (int**)malloc(gridSize * sizeof(int*));
for (int i = 0; i < gridSize; i++) {
gridPtr[i] = (int*)malloc(gridColSize[i] * sizeof(int));
for (int j = 0; j < gridColSize[i]; j++) {
gridPtr[i][j] = grid[i][j];
}
}
int minSum = minPathSum(gridPtr, gridSize, gridColSize);
printf("The minimum path sum is: %d\n", minSum);
// 释放动态分配的内存
for (int i = 0; i < gridSize; i++) {
free(gridPtr[i]);
}
free(gridPtr);
return 0;
}
Python3版本
def minPathSum(grid):
if not grid or not grid[0]:
return 0
m, n = len(grid), len(grid[0])
dp = [0] * n
# 初始化第一行
dp[0] = grid[0][0]
for j in range(1, n):
dp[j] = dp[j - 1] + grid[0][j]
# 填充其他行
for i in range(1, m):
prev = dp[0]
for j in range(n):
curr = dp[j]
dp[j] = prev + grid[i][j] if j == 0 else min(prev, dp[j]) + grid[i][j]
prev = curr
return dp[n - 1]
# 示例网格
grid = [
[1, 3, 1],[1, 5, 1],
[4, 2, 1]
]
min_sum = minPathSum(grid)
print(f"The minimum path sum is: {min_sum}")
go
// minPathSumOpt 使用滚动数组优化DP方法求解最小路径和
func minPathSumOpt(grid [][]int) int {
if len(grid) == 0 || len(grid[0]) == 0 {
return 0
}
rows, cols := len(grid), len(grid[0])
// 只需要一个一维数组来保存当前行的最小路径和
prevRow := make([]int, cols)
currRow := make([]int, cols)
// 初始化第一列
prevRow[0] = grid[0][0]
for j := 1; j < cols; j++ {
prevRow[j] = prevRow[j-1] + grid[0][j]
}
// 填充剩余的行
for i := 1; i < rows; i++ {
// 交换prevRow和currRow,currRow用于保存当前行的最小路径和
prevRow, currRow = currRow, prevRow
// 初始化当前行的第一列
currRow[0] = prevRow[0] + grid[i][0]
// 填充当前行的剩余列
for j := 1; j < cols; j++ {
// 当前位置的最小路径和取上方和左方位置的最小路径和加上当前位置的值
currRow[j] = min(prevRow[j], currRow[j-1]) + grid[i][j]
}
}
// 返回最后一行的最后一个元素,即最小路径和
return currRow[cols-1]
}
// min 返回两个整数中的较小值
func min(a, b int) int {
if a < b {
return a
}
return b
}
// 示例使用
func main() {
grid := [][]int{
{1, 3, 1},
{1, 5, 1},
{4, 2, 1},
}
minSum := minPathSumOpt(grid)
fmt.Printf("The minimum path sum with rolling array optimization is: %d\n", minSum)
}
说明:
函数功能
minPathSumOpt:使用滚动数组优化DP算法计算从grid左上角到右下角的最小路径和。
步奏
- 初始化两个一维数组
prevRow和currRow。- 填充
prevRow数组作为第一行的最小路径和。- 遍历
grid剩余行,交替使用prevRow和currRow计算最小路径和。- 返回
currRow的最后一个元素作为结果。
复杂度分析
- 时间复杂度:O(mn),其中 m 和 n 分别是网格的行数和列数。仍然需要遍历每个网格位置一次。
- 空间复杂度:O(n),其中 n 是网格的列数。使用滚动数组只需要存储一行的值。
滚动数组优化后的空间复杂度更低,但时间复杂度保持不变。这种优化在处理大规模网格时尤其有用,因为它显著减少了内存的使用。
总结
| 解法 | 思路 | 特点 | 优点 | 缺点 | 时间复杂度 | 空间复杂度 |
|---|---|---|---|---|---|---|
| 朴素DP | 填充DP表,状态转移 | 每个位置的状态取决于上方和左方 | 直观易懂 | 空间占用大 | O(mn) | O(mn) |
| 滚动数组优化DP | 只用一维数组,通过循环更新 | 节省空间,利用上一行的值 | 节省空间 | 编程稍微复杂 | O(mn) | O(n) |
相似题目
| 相似题目 | 难度 | 链接 |
|---|---|---|
| leetcode 349 两个数组的交集 | 简单 | 力扣-349 |
| leetcode 62 不同路径 | 中等 | 力扣-62 |
| leetcode 63 不同路径 II | 中等 | 力扣-63 |
| leetcode 64 最小路径和 | 中等 | 力扣-64 |
| leetcode 120 三角形最小路径和 | 中等 | 力扣-120 |
| leetcode 152 乘积最大子数组 | 中等 | 力扣-152 |
| leetcode 198 打家劫舍 | 中等 | 力扣-198 |
| leetcode 213 打家劫舍 II | 困难 | 力扣-213 |
| leetcode 300 最长递增子序列 | 中等 | 力扣-300 |
| leetcode 309 最佳买卖股票时机含冷冻期 | 中等 | 力扣-309 |
这些题目都涉及到动态规划的思想,有些题目可能需要使用滚动数组进行优化,有些题目则需要根据特定条件调整状态转移方程。通过练习这些题目,可以加深对动态规划的理解和掌握。

欢迎一键三连(关注+点赞+收藏),技术的路上一起加油!!!代码改变世界
关于我:阿里非典型程序员一枚 ,记录在大厂的打怪升级之路。 一起学习Java、大数据、数据结构算法(公众号同名),回复暗号,更能获取学习秘籍和书籍等
—⬇️欢迎关注下面的公众号:
进朱者赤,认识不一样的技术人。⬇️—