作者介绍:10年大厂数据\经营分析经验,现任大厂数据部门负责人。
会一些的技术:数据分析、算法、SQL、大数据相关、python
欢迎加入社区:码上找工作
作者专栏每日更新:
LeetCode解锁1000题: 打怪升级之旅
python数据分析可视化:企业实战案例
备注说明:方便大家阅读,统一使用python,带必要注释,公众号 数据分析螺丝钉 一起打怪升级
LeetCode题目42 “接雨水”要求计算在给定的非负整数数组中,数组中的数字表示高度图,计算下雨后能接多少雨水。本文将详细介绍三种解决这一问题的方法,包括解题思路、详细的代码实现以及算法分析。
题目描述
输入:给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
输出:在此高度图中能接的雨水总量。
示例:
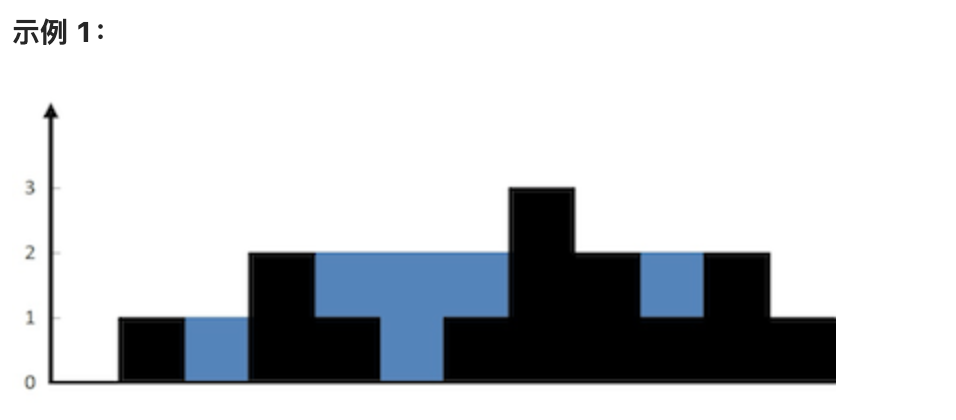
输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出:6
解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
示例 2:
输入:height = [4,2,0,3,2,5]
输出:9
方法一:暴力法
解题步骤
- 对每个元素:计算左边和右边最高的墙的高度。
- 计算接水量:对于每个元素,找到其左右两边最高的墙的较小者,这个值减去当前高度就是该位置能接的水量。
- 求和:将所有位置的接水量累加起来。
代码示例
def trap(height):
"""
使用暴力解法计算接雨水问题
:param height: List[int],表示柱子的高度
:return: int,接到的雨水总量
"""
if not height:
return 0
n = len(height) # 柱子的总数
total_water = 0 # 初始化总雨水量为0
# 遍历每个柱子,除了最左边和最右边的柱子,因为它们不能接雨水
for i in range(1, n - 1):
left_max = 0 # 初始化左边最高柱子高度为0
right_max = 0 # 初始化右边最高柱子高度为0
# 查找左边最高的柱子
for j in range(i):
left_max = max(left_max, height[j])
# 查找右边最高的柱子
for j in range(i + 1, n):
right_max = max(right_max, height[j])
# 计算当前位置最多可以接的雨水量,取决于左右两边较矮的柱子
water = min(left_max, right_max) - height[i]
# 如果计算出的水量大于0,则累加到总雨水量中
if water > 0:
total_water += water
return total_water
# 示例调用
print(trap([0,1,0,2,1,0,1,3,2,1,2,1])) # 输出: 6
算法分析
- 时间复杂度:O(N^2),其中 N 是数组长度。对每个元素进行左右最大值搜索。
- 空间复杂度:O(1)。
方法二:动态规划
解题步骤
- 预处理:创建两个数组
left_max和right_max。left_max[i]存储从左到i的最大高度,right_max[i]存储从右到i的最大高度。 - 计算接水量:遍历每个位置,使用预处理的数组计算该位置能接的水量。
- 求和:累加每个位置的接水量。
代码示例
def trap(height):
"""
使用动态规划解法计算接雨水问题
:param height: List[int],表示柱子的高度
:return: int,接到的雨水总量
"""
if not height:
return 0
n = len(height)
total_water = 0 # 总雨水量
left_max = [0] * n # 左侧最大高度数组
right_max = [0] * n # 右侧最大高度数组
# 填充左侧最大高度数组
left_max[0] = height[0]
for i in range(1, n):
left_max[i] = max(left_max[i - 1], height[i])
# 填充右侧最大高度数组
right_max[n - 1] = height[n - 1]
for i in range(n - 2, -1, -1):
right_max[i] = max(right_max[i + 1], height[i])
# 计算积水量
for i in range(1, n - 1):
water = min(left_max[i], right_max[i]) - height[i]
total_water += water
return total_water
# 示例调用
print(trap([0,1,0,2,1,0,1,3,2,1,2,1])) # 输出: 6
算法分析
- 时间复杂度:O(N),进行了三次线性扫描。
- 空间复杂度:O(N),使用了两个额外的数组来存储左右最大值。
方法三:双指针
解题步骤
- 初始化指针:使用两个指针
left和right,分别指向数组的开头和结尾。 - 移动指针:根据
left_max和right_max的关系决定是移动left还是right指针。 - 计算接水量:根据当前的
left_max和right_max,计算当前指针位置能接的水量,并更新总量。 - 终止条件:当
left大于或等于right时停止。
代码示例
def trap(height):
"""
使用双指针解法计算接雨水问题
:param height: List[int],表示柱子的高度
:return: int,接到的雨水总量
"""
if not height:
return 0
left, right = 0, len(height) - 1 # 初始化左右指针
left_max, right_max = 0, 0 # 初始化左右最大高度
total_water = 0 # 初始化总雨水量
while left < right:
if height[left] < height[right]:
if height[left] >= left_max:
left_max = height[left] # 更新左侧最大高度
else:
total_water += left_max - height[left] # 计算左侧的积水
left += 1 # 移动左指针
else:
if height[right] >= right_max:
right_max = height[right] # 更新右侧最大高度
else:
total_water += right_max - height[right] # 计算右侧的积水
right -= 1 # 移动右指针
return total_water
# 示例调用
print(trap([0,1,0,2,1,0,1,3,2,1,2,1])) # 输出: 6
算法分析
- 时间复杂度:O(N),只需遍历数组一次。
- 空间复杂度:O(1),使用了常数空间。
总结
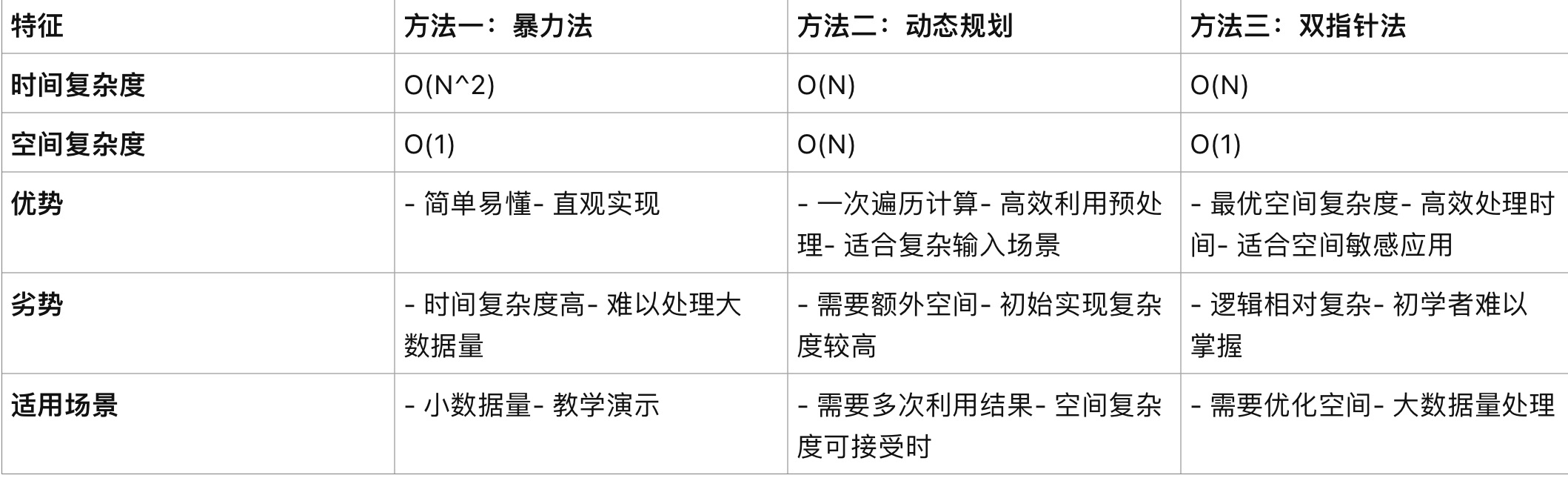
这三种方法从暴力法到优化的双指针法逐步提高了效率和降低了复杂度。在实际应用中,选择哪种方法取决于对时间和空间效率的具体需求。如果需要快速解决问题并且可以使用一些额外空间,动态规划是一个不错的选择;如果对空间有严格限制,双指针法提供了最优的解决方案。