递归 python

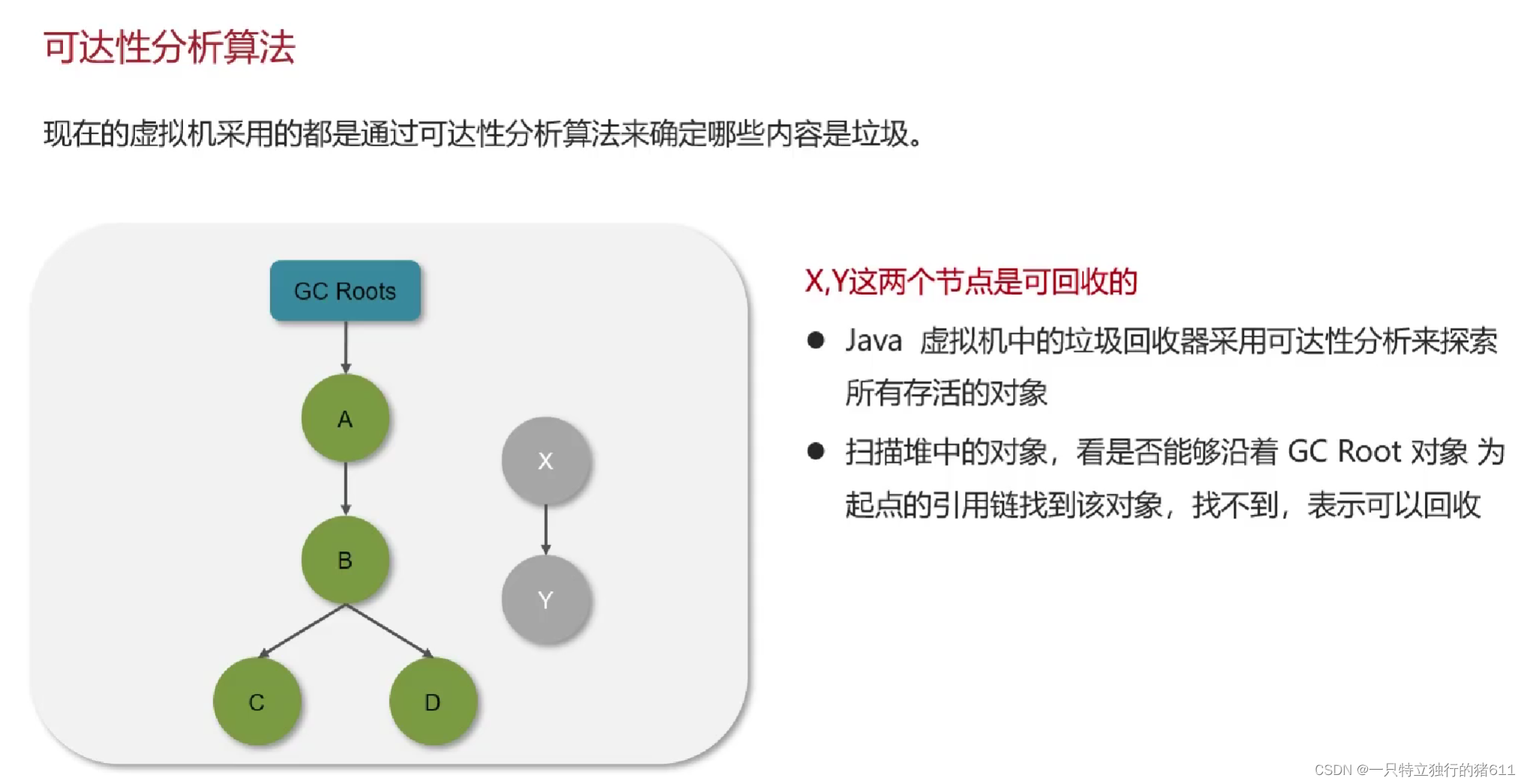
↵一、简单理解

解决问题的一种方法，它将问题不断的分成更小的子问题，直到子问题可以用普通的方法解决。通常情况下，递归会使用一个不停调用自己的函数。

【注】：每一次递归调用都是在解决一个更小的问题，如此进行下去，直到问题本身不能在简化为止

例子：

1.列表元素之和

# 求列表元素之和
def sumList(numlist):
    '''
    循环计算列表和
    :param numlist:数值列表
    :return: 和
    '''
    sum = 0
    for num in numlist:
        sum += num
    return sum


def listnum(numlist):
    '''
    递归计算列表和
    :param numlist: 数值列表
    :return: 和
    '''
    if len(numlist) == 1:
        return numlist[0]
    else:
        return numlist[0] + listnum(numlist[1:])


if __name__ == "__main__":
    numlist = [1, 2, 3, 4, 5, 6]
    a = sumList(numlist)
    b = listnum(numlist)
    print("循环计算结果：%f,递归计算结果：%f" % (a, b))

2.整数转换进制

# 将整数转换成以2-16为进制基数的字符串
def toStr(n, base):
    '''
    将输入的整数n转换成2-16任意进制的字符串
    :param n: 任意正整数
    :param base: 2-16中进制
    :return: 转换好的字符串
    '''
    convertString = "0123456789ABCDEF"
    if n < base:
        return convertString[n]
    else:
        return toStr(n // base, base) + convertString[n % base]


if __name__ == "__main__":
    n = 10
    base = 2
    print("十进制数：%d 转换成二进制数：%s" % (n, toStr(n,base)))#字符的拼接

另外不使用字符拼接的方式

from main import Stack

# 将整数转换成以2-16为进制基数的字符串
rStack = Stack()


def toStr(n, base):
    '''
    将输入的整数n转换成2-16任意进制的字符串,不使用字符拼接，而是通过栈帧
    :param n: 任意正整数
    :param base: 2-16中进制
    :return: 转换好的数值存储栈帧
    '''
    convertString = "0123456789ABCDEF"
    if n < base:
        rStack.push(convertString[n])
    else:
        rStack.push(convertString[n % base])
        toStr(n // base, base)
    return rStack


if __name__ == "__main__":
    n = 100
    base = 2
    numStack = toStr(n, base)
    print("整数%d转换为%d进制为：" % (n, base), end="")
    while numStack.size() >= 1:
        print(numStack.pop(), end="")

二、可视化

使用python中的画图工具进行简单递归程序的绘画，从而理解递归的概念

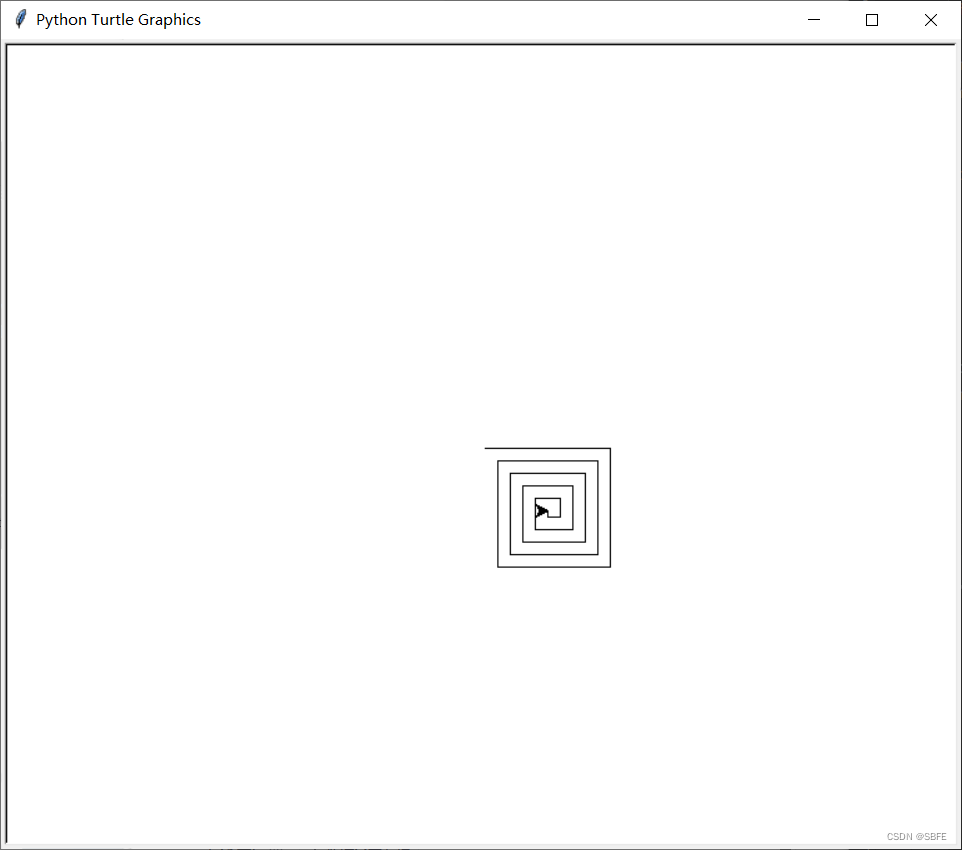
1.螺旋线

#用turtle模块递归的绘制螺旋线
from turtle import *

myTurtle = Turtle()
myWin = myTurtle.getscreen()


def drawSpiral(myTurtle, lineLen):
    if lineLen > 0:
        myTurtle.forward(lineLen)
        myTurtle.right(90)
        drawSpiral(myTurtle, lineLen - 5)


drawSpiral(myTurtle, 100)
myWin.exitonclick()#用户在窗口内再次点击之后，程序清理并退出

2.分形树

#无法绘画出来的
from turtle import *

myTurtle = Turtle()
myWin = myTurtle.getscreen()


def tree(brancheLen, t):
    if brancheLen > 5:
        t.forward(brancheLen)
        t.right(20)
        tree(brancheLen-15,t)
        t.left(40)
        tree(brancheLen-10,t)
        t.right(20)
        t.backward(brancheLen)

t = Turtle()
myWin = t.getscreen()
t.left(90)
t.up()
t.backward(100)
t.down
tree(110,t)
myWin.exitonclick()

chatGPT中给的代码

#能绘画出来
import turtle

def draw_branch(t, length):
    if length > 5:
        t.forward(length)  # 绘制主干
        t.right(20)  # 右转一定角度
        draw_branch(t, length - 15)  # 递归绘制右侧分支
        t.left(40)  # 左转一定角度
        draw_branch(t, length - 15)  # 递归绘制左侧分支
        t.right(20)  # 右转一定角度
        t.backward(length)  # 返回原点

def main():
    # 设置窗口和画笔
    window = turtle.Screen()
    window.bgcolor("white")
    t = turtle.Turtle()
    t.speed(0)  # 设置绘制速度为最快

    # 调整画笔位置和方向
    t.left(90)
    t.up()
    t.backward(200)
    t.down()

    # 绘制分形树
    draw_branch(t, 100)

    # 等待用户点击关闭窗口
    turtle.mainloop()

if __name__ == "__main__":
    main()

3.谢尔平斯基三角形

chatGPT所给的代码---可运行

import turtle

def draw_triangle(t, order, size):
    if order == 0:
        for _ in range(3):
            t.forward(size)
            t.left(120)
    else:
        draw_triangle(t, order - 1, size / 2)
        t.forward(size / 2)
        draw_triangle(t, order - 1, size / 2)
        t.backward(size / 2)
        t.left(60)
        t.forward(size / 2)
        t.right(60)
        draw_triangle(t, order - 1, size / 2)
        t.left(60)
        t.backward(size / 2)
        t.right(60)

def main():
    # 设置窗口和画笔
    window = turtle.Screen()
    window.bgcolor("white")
    t = turtle.Turtle()
    t.speed(0)  # 设置绘制速度为最快

    # 调整画笔位置和方向
    t.up()
    t.goto(-200, -150)
    t.down()

    # 绘制谢尔平斯基三角形
    draw_triangle(t, 5, 400)

    # 隐藏画笔
    t.hideturtle()

    # 等待用户点击关闭窗口
    turtle.mainloop()

if __name__ == "__main__":
    main()

b站上所学

# 绘制谢尔平斯基三角形
#B站--python递归三部曲（基于turtle实现可视化）
import turtle

t = turtle.Turtle()


def get_midpoint(a, b):
    '''
    得到两点的中点坐标
    :param a: 坐标点（元组）
    :param b: 坐标点（元组）
    :return: 中点坐标（元组）
    '''
    ax, ay = a
    bx, by = b
    return ((ax + bx) / 2, (ay + by) / 2)


def draw_triangle(a, b, c):
    '''
    绘制以a，b，c为顶点的三角形
    :param a: 顶点坐标（元组）
    :param b: 顶点坐标（元组）
    :param c: 顶点坐标（元组）
    :return: 无返回值
    '''
    ax, ay = a
    bx, by = b
    cx, cy = c

    t.penup()  # 提起画笔
    t.goto(a)  # 画笔移动到a点的位置
    t.pendown()  # 落下画笔
    t.goto(b)  # 画出ab线段
    t.goto(c)  # 画出bc线段
    t.goto(a)  # 画出ca线段

    t.penup()


def draw_sierpinski(triangle, depth):
    a, b, c = triangle  # triangle包括三个顶点的元组
    draw_triangle(a, b, c)

    if depth == 0:
        return
    else:
        d = get_midpoint(a, b)
        e = get_midpoint(b, c)
        f = get_midpoint(c, a)
        adf = (a, d, f)
        dbe = (d, b, e)
        fec = (f, e, c)
        draw_sierpinski(adf, depth - 1)
        draw_sierpinski(dbe, depth - 1)
        draw_sierpinski(fec, depth - 1)

if __name__ == "__main__":
    triangle = ((-200,-100),(0,200),(200,-100))
    draw_sierpinski(triangle,4)

4.汉诺塔

不能可视化的

#B站---python递归三部曲（基于turtle实现可视化）
#汉诺塔
def moveDisk(diskIndex,fromPole,toPole):
    '''
    从起始塔向目标塔移动圆环
    :param diskIndex:圆环
    :param fromPole:起始塔
    :param toPole:目标塔
    :return:无
    '''
    print_str = 'Move disk %s from %s to %s' %(diskIndex,fromPole,toPole)
    print(print_str)

def moveTower(height,fromPole,withPole,toPole):
    '''
    汉诺塔的递归调用函数
    :param height: 汉诺塔高度
    :param fromPole: 起始塔
    :param withPole: 中转塔
    :param toPole: 目标塔
    :return:
    '''
    if height == 1:
        moveDisk(1,fromPole,toPole)
    else:
        moveTower(height-1,fromPole,toPole,withPole)
        moveDisk(height,fromPole,toPole)
        moveTower(height-1,withPole,fromPole,toPole)

if __name__ == "__main__":
    moveTower(3,"A","B","C")

能可视化的

#自己对着B站视频写的一半，但是无法正确跑，不过注释都是正确的意思
import turtle


def set_plate(i):
    '''
    绘制第i层圆盘
    :return:
    '''
    size = 20  # 圆盘转弯半径基数
    l = size * (i + 2)  # 第i层圆盘半径

    t = turtle.Turtle()
    t.hideturtle()  # 隐藏画笔
    t.penup()  # 提起画笔

    t.left(90)  # 每次先逆时针旋转90度，新建的左转90度为设置时的图案。
    t.begin_poly()  # 绘制记录
    t.forward(l)  # 向前走40
    t.circle(size, 180)  # 画一个半径为20，角度为180的弧
    t.forward(l * 2)
    t.circle(size, 180)
    t.forward(l)
    t.end_poly()  # 结束记录

    turtle.register_shape("plate_%s" % i, p)  # 取出记录的情况，给不同层的圆盘赋值不同的名称


def set_tower():
    '''
    绘制塔
    :return:
    '''
    # 塔的参数：宽、高、转弯半径
    tower_width = 100
    tower_height = 200
    tower_radius = 10

    t = turtle.Turtle()
    t.hideturtle()  # 隐藏画笔
    t.penup()  # 提起画笔

    t.left(90)
    t.begin_poly()
    t.forward(tower_width)
    t.circle(tower_radius, 180)
    t.forward(tower_width - tower_radius)
    t.right(90)
    t.forward(tower_height)
    t.circle(tower_radius, 180)
    t.forward(tower_height)
    t.right(90)
    t.forward(tower_width - tower_radius)
    t.circle(tower_radius, 180)
    t.forward(tower_width)
    t.end_poly()
    turtle.register_shape("tower")


def draw_towers():
    # 塔的参数：塔之间的距离，塔的海拔高度
    tower_distance = 250
    tower_altitude = -100
    set_tower()
    tower = turtle.Turtle("tower")
    tower.speed(0)  # 0是最快的速度
    tower.penup()
    tower.goto(-tower_distance, tower_altitude)  # 移动到（-250，-100）位置
    tower.stamp()  # 一直显示出来
    tower.goto(0, tower_altitude)
    tower.stamp()
    tower.goto(tower_distance, tower_altitude)


if __name__ == "__main__":
    draw_towers()
    set_plate(1)

    plate = turtle.Turtle("plate_1")
    plate.forward(200)
    turtle.done()

B站博主所写代码参考网址：需要魔法（可参考网络代理文章）

#能可视化代码，但是turtle库的绘制方法不熟悉
import turtle

# ==============
#  常量设置
# ==============
N = 7  # 汉诺塔层数限制

BasePL = 12  # plate的大小基数，修改这个能够调整plate的大小
TowerP = 5  # Tower的线宽
TowerW = 110  # Tower的底座宽度
TowerH = 200  # Tower的高度
TowerSpace = 260  # Tower的之间的距离，从中心到中心
HORIZON = -100  # Tower的底座高度，用于定位
# 动画速度，5是比较适中的速度
PMS = 5

# 优化处理
Isjump = True

POLES = {
    "1": [],
    "2": [],
    "3": [],
}
PLATES = []  # 存储所有圆盘对象

# 塔的颜色
LineColor = "black"
# 多个盘子的颜色
FillColors = [
    "#d25b6a",
    "#d2835b",
    "#e5e234",
    "#83d05d",
    "#2862d2",
    "#35b1c0",
    "#5835c0"
]
# 建立窗体
SCR = turtle.Screen()
# SCR.tracer()
SCR.setup(800, 600)  # 设置窗体大小


# 设置圆盘形状
def set_plate(pi=0):
    _pi = pi + 2
    t = turtle.Turtle()
    t.hideturtle()
    t.speed(0)
    t.penup()
    t.begin_poly()
    t.left(90)
    t.forward(BasePL * _pi)
    t.circle(BasePL, 180)
    t.forward(BasePL * 2 * _pi)
    t.circle(BasePL, 180)
    t.forward(BasePL * _pi)
    t.end_poly()
    p = t.get_poly()
    pname = 'plate_%s' % pi
    SCR.register_shape(pname, p)


# 设置塔柱形状
def set_tower():
    t = turtle.Turtle()
    t.hideturtle()
    t.speed(0)
    t.penup()

    t.begin_poly()
    t.left(90)
    t.forward(TowerW)
    t.circle(-TowerP, 180)
    t.forward(TowerW)
    t.forward(TowerW)
    t.circle(-TowerP, 180)
    t.forward(TowerW - TowerP / 2)

    t.left(90)
    t.forward(TowerH)
    t.circle(-TowerP, 180)
    t.forward(TowerH)
    t.end_poly()
    p = t.get_poly()
    SCR.register_shape('tower', p)


# 绘制塔柱
def draw_towers():
    set_tower()
    for tx in [-TowerSpace, 0, TowerSpace]:
        t3 = turtle.Turtle('tower')
        t3.penup()
        t3.goto(tx, HORIZON)


# 绘制圆盘
def draw_plates(pn=4):
    plates = []
    for i in range(pn):
        set_plate(i)
        _plate = 'plate_%s' % i
        _p = turtle.Turtle(_plate)
        _colorIdx = i % len(FillColors)
        _color = FillColors[_colorIdx]

        _p.color(_color, _color)
        _p.speed(PMS)
        plates.append(_p)
    # 反序，大的在前，小的在后
    global PLATES
    PLATES = plates[:]


# 绘制移动过程
def draw_move(diskIndex, fromPindex, toPindex):
    p = PLATES[diskIndex - 1]
    index_loc = {
        "A": 1,
        "B": 2,
        "C": 3
    }
    toP = index_loc.get(toPindex, None)
    fromP = index_loc.get(fromPindex, None)

    p.penup()

    mx = (toP - 2) * TowerSpace
    my = HORIZON + len(POLES[str(toP)]) * BasePL * 2

    if fromP != None:
        POLES[str(fromP)].remove(p)
        if Isjump:
            px, py = p.pos()
            p.goto(px, TowerH + py)
            p.goto(mx, TowerH + py)

    p.goto(mx, my)
    POLES[str(toP)].append(p)


# 将所有圆盘移动到起点
def movetoA(n, fromPindex):
    for i in range(n, 0, -1):
        draw_move(i, None, fromPindex)


# 移动指定层圆盘diskIndex，从fromPole出发，到达toPole
def moveDisk(diskIndex, fromPole, toPole):
    """
    :param diskIndex: 圆盘的索引（从上往下，第一层为1，第二层为2、、、第n层为n）
    :param fromPole: 出发的柱子（起点）
    :param toPole: 要到达的柱子（终点）
    :return:
    """
    draw_move(diskIndex, fromPole, toPole)


# 核心函数，入口
def moveTower(height, fromPole, withPole, toPole):
    """
    :param height: 汉诺塔高度——层数
    :param fromPole: 出发的柱子（起点）
    :param withPole: 进过的柱子（中转点）
    :param toPole: 要到达的柱子（终点）
    :return:
    """
    if height == 1:
        # 基础情形：一层的汉诺塔
        moveDisk(1, fromPole, toPole)
        return

    # 先将圆盘1到n - 1看作一个整体从起点塔移动到中转塔（用目标塔作为本步骤的中转）
    moveTower(height - 1, fromPole, toPole, withPole)
    # 再将圆盘n从起点塔A移动到目标塔C
    moveDisk(height, fromPole, toPole)
    # 最后将圆盘1到n - 1看作一个整体从中转塔移动到目标塔（用起点塔作为本步骤的中转）
    moveTower(height - 1, withPole, fromPole, toPole)


if __name__ == '__main__':
    # 调用
    # 三层汉诺塔，A为出发柱子，B为中转柱子，C为目标柱子
    n = N

    SCR.tracer(0)
    draw_towers()
    draw_plates(n)
    movetoA(n, "A")
    SCR.tracer(1)

    # SCR.delay(3)

    moveTower(n, "A", "B", "C")
    turtle.done()