目录
一、堆
1、简介
2、堆的模拟实现
a、向下调整堆
b、向上调整堆
c、插入元素
d、删除堆的根结点
e、获得堆顶元素
二、优先级队列
1、简介
2、常用方法
3、Top-k问题
一、堆
1、简介
堆也是一种数据结构,将一组数据集合按照完全二叉树的方式存储起来,堆分为大根堆和小根堆,如果根结点总是大于孩子结点就是大根堆,如果根结点总是小于孩子结点就是小根堆。
如下的小根堆在一维数组进行存放:
2、堆的模拟实现
堆用一维数组进行存储,所以需要定义一个一维数组的属性,还需要定义一个变量来表示堆的当前大小。
以下方法均以创建大根对为例。
public int[] elem;
public int usedSize;
public Heap() {
elem=new int[11];
usedSize=0;
}a、向下调整堆
首先需要传入根结点坐标i,那么左孩子的坐标为2i+1,如果左孩子坐标未越界,并且如果右孩子2i+2也未越界,求左右孩子的最大值比根结点还大,就要进行交换,然后根的下标等于孩子结点的下标,孩子结点的下标为2i+1,然后再进行循环判断越界,如果左右孩子的最大值小于根结点的值,那么不用继续调整,退出循环即可。
private void shiftDown(int root,int len) {
int child=2*root+1;
while(child<len){
//有右孩子并且右孩子的值大于根结点
if(child+1<len&&elem[child]<elem[child+1]){
child++;
}
if(elem[child]>elem[root]){
int temp=elem[child];
elem[child]=elem[root];
elem[root]=temp;
root=child;
child=2*root+1;
}else{
break;
}
}
}向下调整方法的时间复杂度为O(log2 n)
那么就可以利用向下调整来创建一个堆,首先初始化堆的内存数组,然后从最后一个子树的根结点开始调用向下调整的方法,直到根结点,以确保最后整棵树都符合堆的条件。
public void createHeap(int[] array) {
for(int i=0;i<array.length;i++){
elem[i]=array[i];
usedSize++;
}
for(int i=(elem.length-1-1)/2;i>=0;i--){
shiftDown(i,usedSize);
}
}那么利用向下调整来创建一个堆的时间复杂度如何推导?
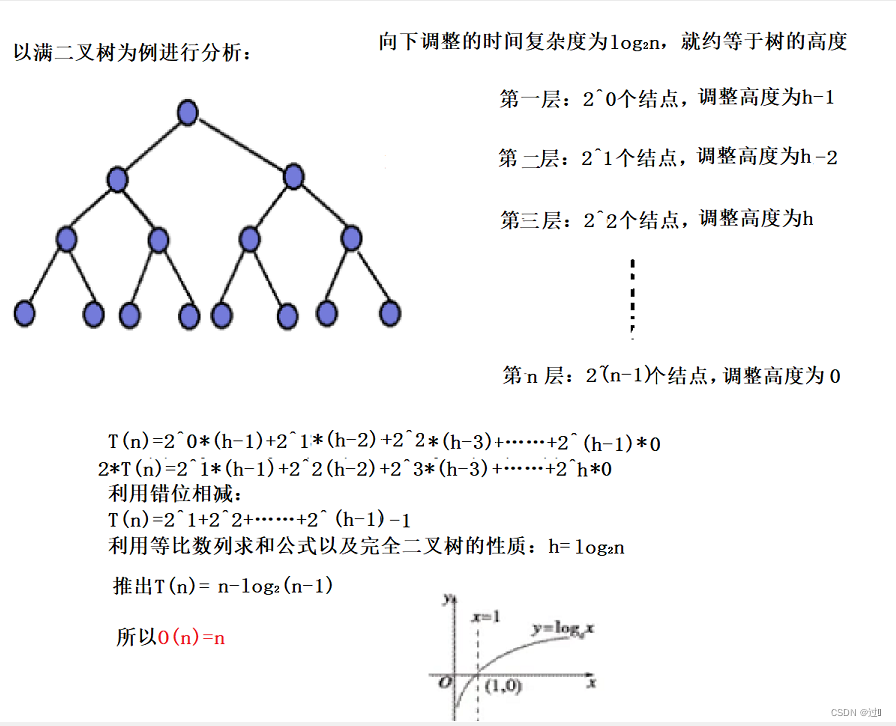
b、向上调整堆
传入要调整的孩子结点的下标i,然后利用(i-1)/2计算出根结点坐标root,若根结点的元素小于等于孩子结点就退出循环,否则进行交换,然后让孩子结点的下标等于根结点,根结点坐标为(孩子结点下标-1)/2,只要根结点坐标不小于0就继续循环。
private void shiftUp(int child) {
int root=(child-1)/2;
while(root>=0){
if(elem[root]<elem[child]){
int temp=elem[child];
elem[child]=elem[root];
elem[root]=temp;
child=root;
root=(child-1)/2;
}else{
break;
}
}
}向上调整方法的时间复杂度为O(log2 n)
利用向上调整也可以创建堆,传入的下标从0~最后一个孩子结点,时间复杂度的推导方法与向下调整创建堆的方法类似,可以推出向上调整创建时间复杂度的方法为O(n*log2 n) 。
c、插入元素
首先判断堆是否已满,若未满则将元素插入到最后一个孩子结点之后,然后存储的数组有效长度加一,然后传入插入元素的位置下标进行向上调整。
public void push(int val) {
if(isFull()){
System.out.println("堆已满");
}
elem[usedSize++]=val;
shiftUp(usedSize-1);
}
private void shiftUp(int child) {
int root=(child-1)/2;
while(root>=0){
if(elem[root]<elem[child]){
int temp=elem[child];
elem[child]=elem[root];
elem[root]=temp;
child=root;
root=(child-1)/2;
}else{
break;
}
}
}
public boolean isFull() {
return usedSize == elem.length;
}d、删除堆的根结点
如果堆不为空,就将最后一个结点与根结点进行交换,存储堆的数组的有效长度减一,然后传入根结点向下调整。
public void pollHeap() {
if(isEmpty()){
System.out.println("堆为空");
}
int temp=elem[0];
elem[0]=elem[usedSize-1];
elem[usedSize-1]=temp;
usedSize--;
shiftDown(0,usedSize);
}e、获得堆顶元素
若堆非空,直接取出堆存储数组下标为0的元素。
public int peekHeap() {
if(isEmpty()){
System.out.println("堆为空");
}
return elem[0];
}二、优先级队列
1、简介
优先级队列也是一种队列,普通队列具有先进先出的特点,优先级队列中存放的元素带有优先级,是优先级高的元素先出队。
优先级队列主要分为PriorityQueue和PriorityBlockingQueue,前者是线程不安全的,后者是线程安全的,本文主要讲解前者。
优先级队列底层是利用堆来实现。
使用优先级队列有以下注意点:
- 使用PriorityQueue必须导入其所在的包:import java.util.PriorityQueue。
- PriorityQueue中存放的元素必须能比较大小,否则就会抛出异常。
- 不能插入null对象,否则抛出异常。
- 没有容量限制,内部可以自动扩容。
- 进行插入元素和删除元素的时间复杂度为O(log2 n)。
- PriorityQueue底层依靠堆实现。
- PriorityQueue默认存放的元素是以小根堆的形式存储。
2、常用方法
构造器方法:

根据PriorityQueue底层的源码,如果PriorityQueue的构造方法可以传入比较器,或者存储的对象就必须实现Comparable接口并重写CompareTo方法,否则就会抛出异常。
例如在优先级队列中添加学生类的时候,就可以定义一个比较器来比较学号大小。
class CompareSno implements Comparator<Student>{
@Override
public int compare(Student o1, Student o2) {
return o1.getSno()-o2.getSno();
}
}
public class TestPriorityQueue {
public static void main(String[] args) {
Student student1 = new Student(1);
Student student2 = new Student(12);
Student student3 = new Student(9);
Queue<Student> stu=new PriorityQueue<>(new CompareSno());
stu.offer(student1);
stu.offer(student2);
stu.offer(student3);
while(!stu.isEmpty()){
System.out.println(stu.poll().toString());
}
}
}
运行结果:
普通方法 :
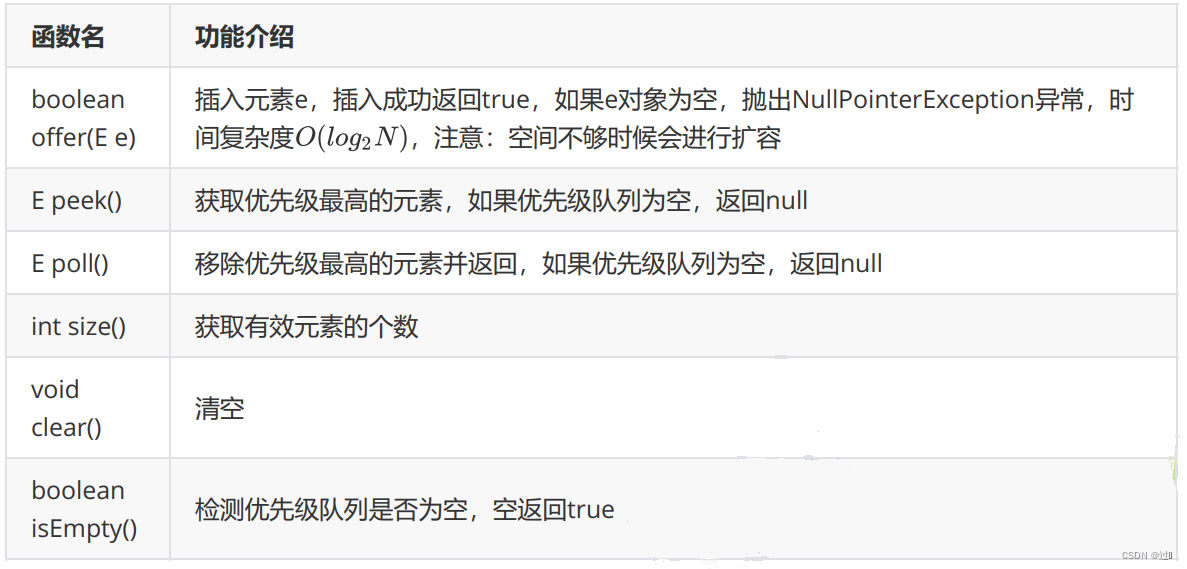
3、Top-k问题
TOP-K问题:即求数据集合中前K个最大的元素或者最小的元素,一般情况下数据量都比较大。
例如:求世界五百强企业,中国富豪榜等等。
问题分析:假设要求前k个元素,在未学习堆之前,我们可能会对数据集合进行排序然后取前k个元素存放到数组中,那么在学了堆之后就可以创建一个能存放数据集合k个元素的小根堆,然后数据集合接着从第k+1个元素遍历,如果遇到比对顶元素大的就将该元素存放为堆顶元素 ,因为在小根堆中堆顶元素是最小的,如果比十个最大的当中的最小的要大,那么就要加入这个堆中,原来的堆顶元素删除,然后依次向后遍历。同理如果要求后k个元素,那么就创建一个能存放数据集合k个元素的大根堆。
例如:求最小的k个数
由于优先级队列是小根堆,而这个题需要大根堆所以就创建优先级队列时传入了比较器,使其变为大根堆。
public int[] smallestK(int[] arr, int k) {
int[] nums=new int[k];
if(arr==null || k==0){
return nums;
}
Queue<Integer> que = new PriorityQueue<>(new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return o2-o1;
}
});
for(int i=0;i<k;i++){
que.offer(arr[i]);
}
for(int i=k;i<arr.length;i++){
if(arr[i]<que.peek()){
que.poll();
que.offer(arr[i]);
}
}
for(int i=0;i<k;i++){
nums[i]=que.poll();
}
return nums;
}