一、K-means算法概述

K-means算法是一种非常经典的聚类算法，其主要目的是将数据点划分为K个集群，以使得每个数据点与其所属集群的中心点（质心）的平方距离之和最小。这种算法在数据挖掘、图像处理、模式识别等领域有着广泛的应用。

二、K-means算法的基本原理

K-means算法的基本原理相对简单直观。算法接受两个输入参数：一是数据集，二是用户指定的集群数量K。算法的输出是K个集群，每个集群都有其中心点以及属于该集群的数据点。

K-means算法的执行过程如下：

1. 初始化：随机选择K个点作为初始集群中心（质心）。
2. 分配数据点到最近的集群：对于数据集中的每个点，计算其与各个质心的距离，并将其分配到距离最近的质心所对应的集群中。
3. 重新计算质心：对于每个集群，计算其内所有数据点的平均值，并将该平均值设为新的质心。
4. 迭代优化：重复步骤2和3，直到满足某个终止条件（如质心的变化小于某个阈值，或者达到最大迭代次数）。

图解说明：

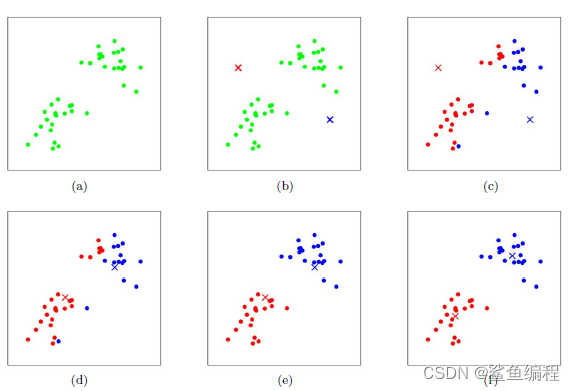
图a表示初始的数据集，在图b中随机找到两个类别质心，接着执行上述的步骤二，得到图c的两个集群，但此时明显不符合我们的要求，因此需要进行步骤三，得到新的类别质心（图d），重复的进行多次迭代（如图e和f），直到达到不错的结果。

三、K-means算法的数学表达

K-means 算法是一种迭代求解的聚类分析算法，其目标是将 $n$ 个观测值划分为 $k$（$k\le n$）个聚类，以使得每个观测值属于离它最近的均值（聚类中心或聚类质心）对应的聚类，以作为聚类的标准。

数学公式

1. 数据表示

   设数据集 D = { x 1 , x 2 , … , x n } D = \{x_1, x_2, \ldots, x_n\} D={ x1​,x2​,…,xn​}，其中每个数据点 $x_i$ 是一个 $d$ 维向量。

2. 聚类中心

   假设我们要将数据集聚成 $k$ 类，那么就会有 $k$ 个聚类中心，记作 { μ 1 , μ 2 , … , μ k } \{\mu_1, \mu_2, \ldots, \mu_k\} { μ1​,μ2​,…,μk​}。

3. 目标函数

   K-means 算法的目标是最小化每个数据点与其所属聚类的聚类中心之间的距离之和。这个距离通常使用欧几里得距离来衡量。目标函数可以表示为：

   $$J=\sum _{j=1}^k\sum _{i=1}^n{w}_{ij}\Vert x_i-{\mu }_j{\Vert }^2$$

   其中， w i j w_{ij}