今天的题，最后一题忘公式了，卡了一会推出来了

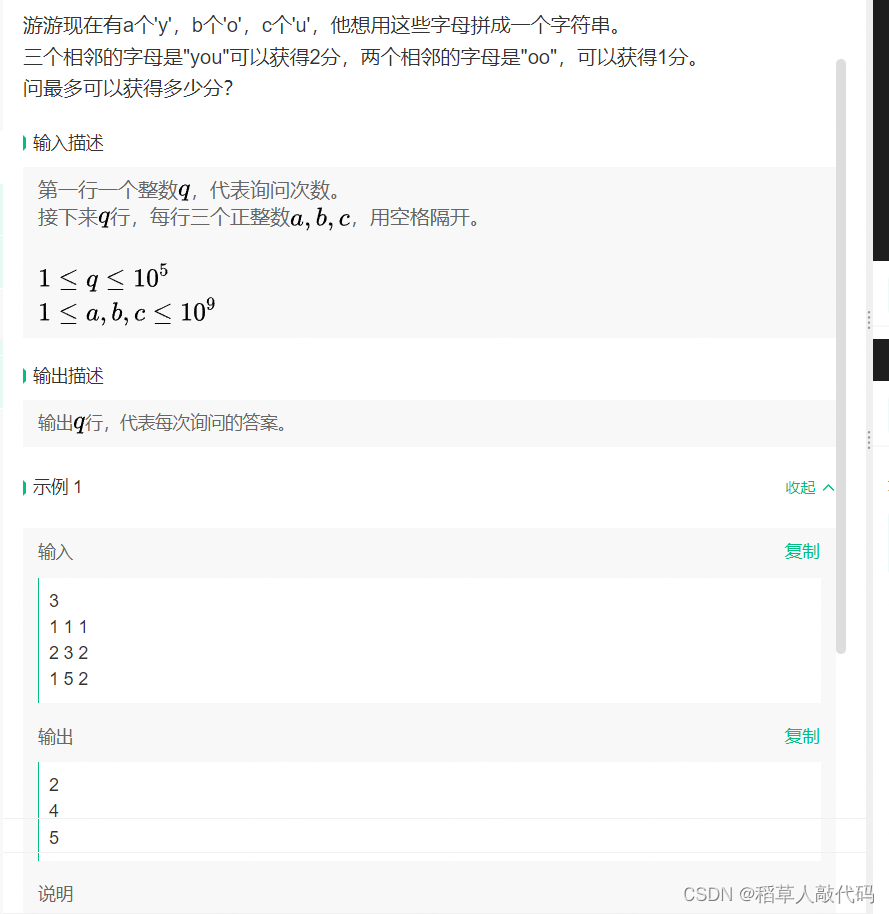
1、游游的you

思路：

看清题目意思就行，这里的相邻两个o可以重复算，也就是说，“ooo”算2分。
先算you的得分，再算oo
对了，不开long long见祖宗！

代码：

#include <iostream>
#include<algorithm>

using namespace std;

int main() {
    long long a, b, c;
    int t;
    cin >> t;
    while (t--) {
        cin >> a >> b >> c;
        long long ans = 0;
        int k = min(min(a, b), c);
        ans = k * 2;
        ans = ans + max((long long)b - k - 1, (long long)0);
        cout << ans << endl;
    }

    return 0;
}

2.腐烂的苹果

思路：

一眼bfs。
从好的苹果开始往外面扩展也可以，从坏的苹果往外扩展也可以。
我选后者。先将所有的坏苹果放在一个队列里，每次都一次性把队列里的元素全部取出来去“感染”。每一次都是一分钟。然后再把这次感染的苹果放回到队列里，用来下次感染就行。

代码：

#define _CRT_SECURE_NO_WARNINGS 1
typedef pair<int, int> PII;
int dx[] = { 0,0,-1,1 };
int dy[] = { -1,1,0,0 };
const int N = 1e3 + 10;
int g[N][N];
bool st[N][N];

class Solution {
public:
    int bfs(vector<vector<int> >& grid) {
        int m = grid.size();
        int n = grid[0].size();
        int cnt = 0;//计算完好苹果的数量
        queue<PII> q;
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (grid[i][j] == 2) {
                    q.push({ i,j });
                    st[i][j] = true;
                }
                else if (grid[i][j] == 1)cnt++;
            }
        }
        int t = -1;//因为开始腐烂的苹果也会算时间，所以初始化为-1，自己手动模拟一下就知道了
        while (!q.empty()) {
            int sz = q.size();
            // cout<<sz<<endl;
            for (int i = 0; i < sz; i++) {
                auto it = q.front();
                q.pop();
                int x = it.first;
                int y = it.second;
                for (int j = 0; j < 4; j++) {
                    int a = x + dx[j];
                    int b = y + dy[j];
                    if (a >= 0 && a < m && b >= 0 && b < n && !st[a][b] && grid[a][b] == 1) {
                        g[a][b] = 2;
                        cnt--;//每有一个好苹果被感染就-1
                        q.push({ a,b });
                        st[a][b] = true;
                    }
                }
            }
            t++;//时间加1
        }

        if (cnt)return -1;
        return t;

    }
    int rotApple(vector<vector<int> >& grid) {
        return bfs(grid);
    }
};

3.孩子们的游戏

思路：

典型的约瑟夫环问题。注意题目要求空间复杂度为O(1),理论上来说也就意味着用队列，链表，数组的方法都是错的！
这里可以通过著名的递推公式去解决：
f(n,m)=(f（n-1，m）+m)%n
其中，f(n,m)表示剩下n个人除掉报数为m的人之后剩下的一个人的坐标。
举例：n=4，m=2.
从后往前推，当n==1时f(1,2)=0.
当n==2时，f(2,2)=(0+2)%2=0;
当n==3时，f(3,2)=(0+2)%3=2;
当n==4时，f(4,2)=(2+2)%4=0;
所以还有4个人的时候，把报2的人全部干掉，最后一个人的坐标就是0.
再将整个递归过程展开为循环，这样空间复杂度就是O(1)了（递归的参数也算空间复杂度）。
这个公式很少考，记住就行，考场推比较浪费时间。我也是一个一个推，看规律得到的。

代码：

class Solution {
public:
    int f(int n, int m) {//递归公式
        if (n == 1)return 0;
        return (f(n - 1, m) + m) % n;
    }
    int LastRemaining_Solution(int n, int m) {
        int t=0;
        int ans=t;
        int c=1;
        for(int i=2;i<=n;i++){
           c++;
           t=(t+m)%c;
        }
        return t;
    }
};