文章目录
- 前言
- 理解轴的两个角度
- 在维度变化方向上计算
- 降维
- 示例剖析
- 写在最后
前言
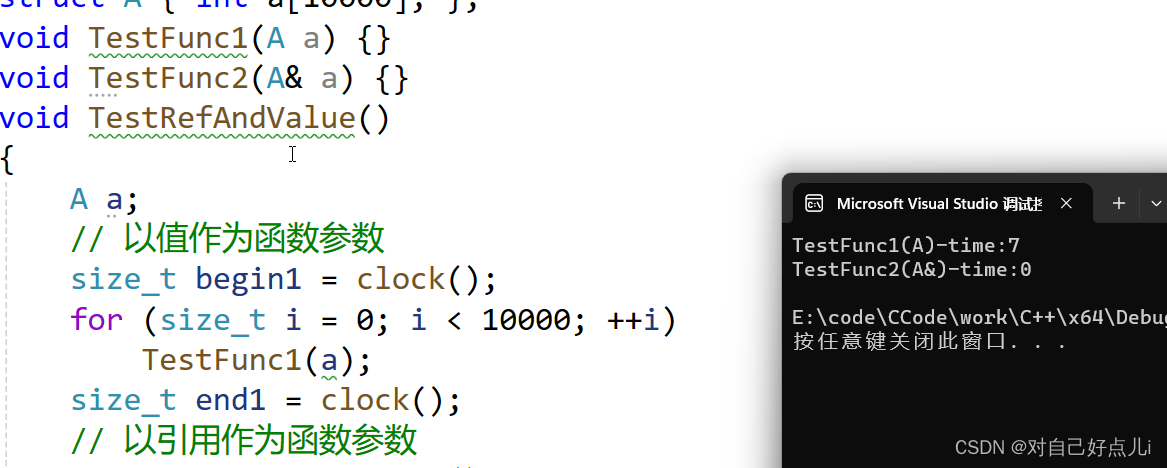
Numpy 是 Python 中一个常用科学计算库,常用来表示向量、矩阵以及多维度数组。在 Numpy 中多对某一个维度(轴)进行相应的操作,这一点经常出错。今天就来讨论一下 Numpy 中的 axis 问题。
axis 从字面来看是轴的意思,在小学阶段,我们就学过坐标系,对轴的这个概念应该都不会陌生。比如,在平面直角坐标系中就有 x 轴 和 y 轴。在NumPy中,array是一个的核心数据结构,用于存储和操作多维数据。array可以是一维的,也可以是多维的。不论是多维数组还是一维数组,其每一个维度表示的都是一个轴。
理解轴的两个角度
对于二维数组有两个轴:axis = 0 和 axis = 1。axis = 0 表示横轴,确切地说是行变换的轴。相应的 axis = 1 表示的是列变化的轴。
imprt numpy as np
matrixA = np.array([[1, 8, 3, 9],
[4, 5, 6, 7]])
np.sum(matrixA, axis=0) # 输出 [5, 13, 9, 16]
在维度变化方向上计算
在这样的一个示例中,matrixA 是一个二维数组,有两个维度,行和列。现在我们要对 matrixA 执行 np.sum 操作,Numpy 参考文档上对于该操作的释义是:Sum of array elements over a given axis. 可以理解为:对横跨指定轴数组元素求和。这里是 axis = 0,因而是对横跨 行 的数组元素求和,也就是在行变化方向上求和。 于是 np.sum(matrixA, axis=0) 的输出结果为 [5, 13, 9, 16]。
降维
还有一种理解方式,对指定轴进行压缩求和。这个例子中就是对行进行压缩求和,将两行压缩成一行,对应位置元素相加,也会得到正确的输出结果。
示例剖析
接下来用三维数组来验证一下我们对于 axis 的理解。三维数组的第一、二、三维度依次是下图中红、绿、蓝三个区域。
imprt numpy as np
a = np.arange(24).reshape((3, 2, 4)) # 利用 np.arange 生成 0~23, 接着用 reshape 修改成维度为 (3, 2, 4) 的array
# a 的输出结果
"""
array([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7]],
[[ 8, 9, 10, 11],
[12, 13, 14, 15]],
[[16, 17, 18, 19],
[20, 21, 22, 23]]])
"""
np.sum(a, axis = 1) # 对第二维度求和
# 输出结果
"""
array([[ 4, 6, 8, 10],
[20, 22, 24, 26],
[36, 38, 40, 42]])
"""

按照 在维度变化方向上计算 来理解,第一维度不变,在第二维度也就是行的变化方向上进行元素相加,于是得到 array([[ 4, 6, 8, 10], [20, 22, 24, 26], [36, 38, 40, 42]])。
按照 降维 来理解,第二维度的多行将被压缩成一行,最后得到的结果也是 array([[ 4, 6, 8, 10], [20, 22, 24, 26], [36, 38, 40, 42]])。
无论是从降维角度还是在维度变化方向上这个角度来看,这些操作本质上都实现了数组的降维。至于选择哪个角度来理解操作,因人而异。
写在最后
如果您发现文章有任何错误或者对文章有任何疑问,欢迎私信博主或者在评论区指出 💬💬💬。
如果大家对于 axis 有更好的理解,欢迎评论区交流。
最后,感谢您的阅读,如果有所收获的话可以给我点一个 👍 哦。