- 🎥 个人主页:Dikz12
- 🔥个人专栏:算法(Java)
- 📕格言:吾愚多不敏,而愿加学
- 欢迎大家👍点赞✍评论⭐收藏
目录
二分查找算法介绍
1.二分查找
题目描述
讲解
编辑
代码实现
2.在排序数组中查找元素的第一个和最后一位置
题目描述
编辑 题解
编辑
代码实现
模版总结
3.山脉数组的峰顶索引
题目描述
题解
代码实现
4.点名
题目描述
题解
代码实现
5.寻找旋转排序数组中的最小值
题目描述
题解
代码实现
二分查找算法介绍
二分查找的使用并不是单单在数组有序的情况下,而是数据能否划分成两段,是否满足“二段性” ;也是细节最多,最容易写出死循环的算法;时间复杂度O(logN),写法模版大致可以分为:
- 朴素的二分查找(局限性)
- 查找左边界
- 查找右边界
写法就在题的里面讲述.
1.二分查找
题目描述

讲解
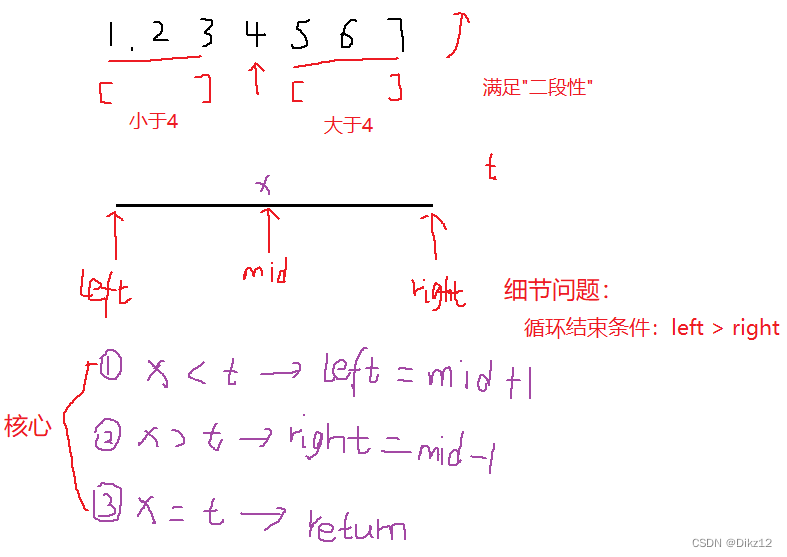
解法:采用最朴素的二分查找.
- 定义 left , right 指针,分别指向数组的左右区间
-
找到待查找区间的中间点 mid ,找到之后分三种情况讨论:
-
arr[mid] == target 说明正好找到,返回 mid 的值;
-
arr[mid] > target 说明 [mid, right] 这段区间都是⼤于 target 的,因此舍去右边区间,在左边 [left, mid -1] 的区间继续查找,即让 right = mid - 1
-
arr[mid] < target 说明 [left, mid] 这段区间的值都是⼩于 target 的,因 此舍去左边区间,在右边 [mid + 1, right] 区间继续查找,即让 left = mid + 1
-
当 left 与 right 错开时,说明整个区间都没有这个数,返回 -1 。
代码实现
public int search(int[] nums, int target) {
int left = 0,right = nums.length - 1;
while(left <= right) {
int mid = left + (right - left) / 2;
if(nums[mid] < target) {
left = mid + 1;
}else if(nums[mid] > target) {
right = mid - 1;
}else{
return mid;
}
}
return -1;
}2.在排序数组中查找元素的第一个和最后一位置
题目描述
 题解
题解
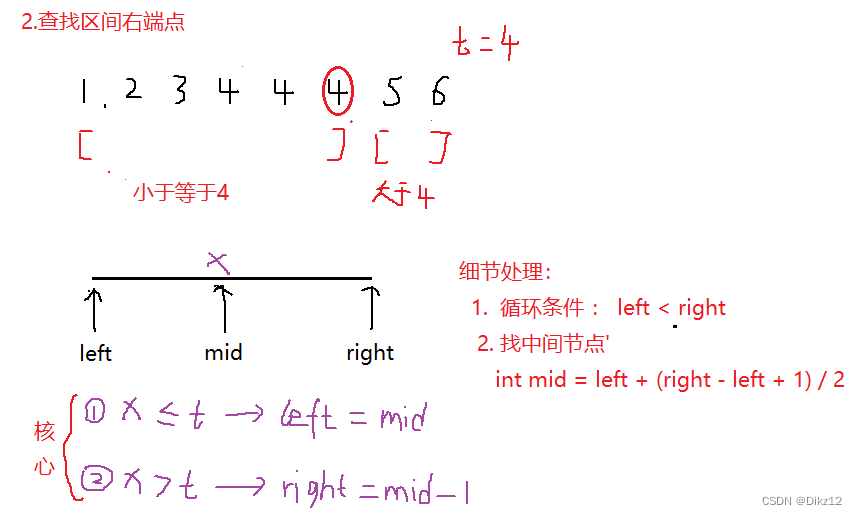
解法:采用查找区间的左端点 和 查找区间的右端点.
1.查找区间左端点.
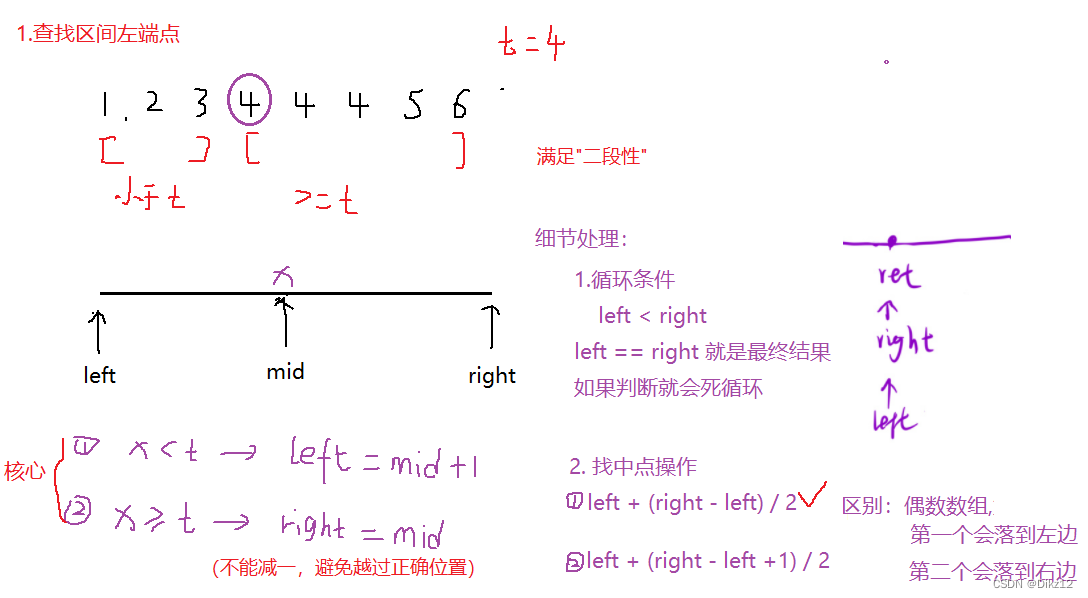
2. 查找区间右端点
代码实现
public int[] searchRange(int[] nums, int target) {
int[] ret = new int[2];
ret[0] = ret[1] = -1;
if(nums.length == 0) {
return ret;
}
//查找左端点
int left = 0,right = nums.length - 1;
while(left < right) {
int mid = left + (right - left) / 2;
if(nums[mid] < target) {
left = mid + 1;
}else {
right = mid;
}
}
if(nums[left] != target) {
return ret;
}else{
ret[0] = right;
}
//查找右端点
// left = 0;
right = nums.length - 1;
while(left < right) {
int mid = left + (right - left + 1) / 2;
if(nums[mid] <= target) {
left = mid;
}else {
right = mid - 1;
}
}
if(nums[left] != target) {
return ret;
}else {
ret[1] = left;
}
return ret;
}模版总结

3.山脉数组的峰顶索引
题目描述

题解

代码实现
public int peakIndexInMountainArray(int[] arr) {
// 删去第一个和最后一个
int left = 1,right =arr.length - 2;
while(left < right) {
int mid = left + (right - left + 1) / 2;
if(arr[mid] > arr[mid - 1]) {
left = mid;
}else {
right = mid - 1;
}
}
return left;
}4.点名
题目描述

题解
解一:暴力解法(直接查询)
解二:借助哈希容器
解三:位运算
解四:高斯求和(数学公式)
解五:二分法
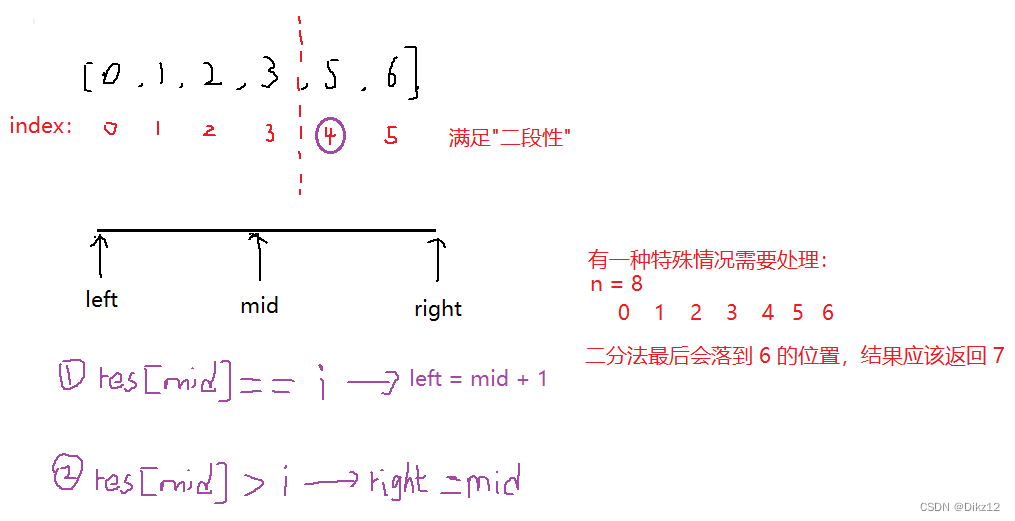
代码实现
public int takeAttendance(int[] records) {
int left = 0,right = records.length - 1;
while(left < right) {
int mid = left + (right - left) / 2;
if(records[mid] == mid) {
left = mid + 1;
}else{
right =mid;
}
}
if(records[left] == left) {
return left + 1;
}
return left;
}5.寻找旋转排序数组中的最小值
题目描述

题解

代码实现
public int findMin(int[] nums) {
int left = 0 ,right = nums.length - 1;
int tmp = nums[right];
while(left < right) {
int mid = left + (right - left) / 2;
if(nums[mid] > tmp) {
left = mid + 1;
}else {
right = mid;
}
}
return nums[left];
}