Vision Transformer (ViT)

概述

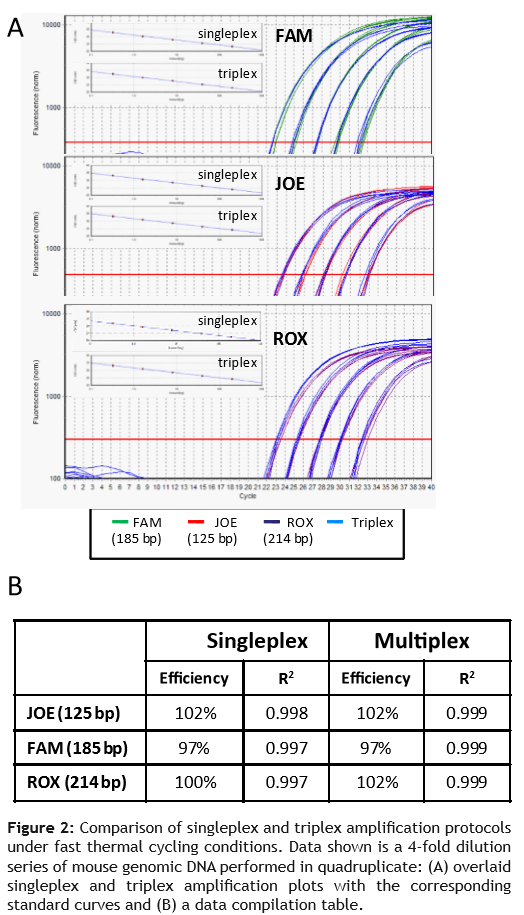
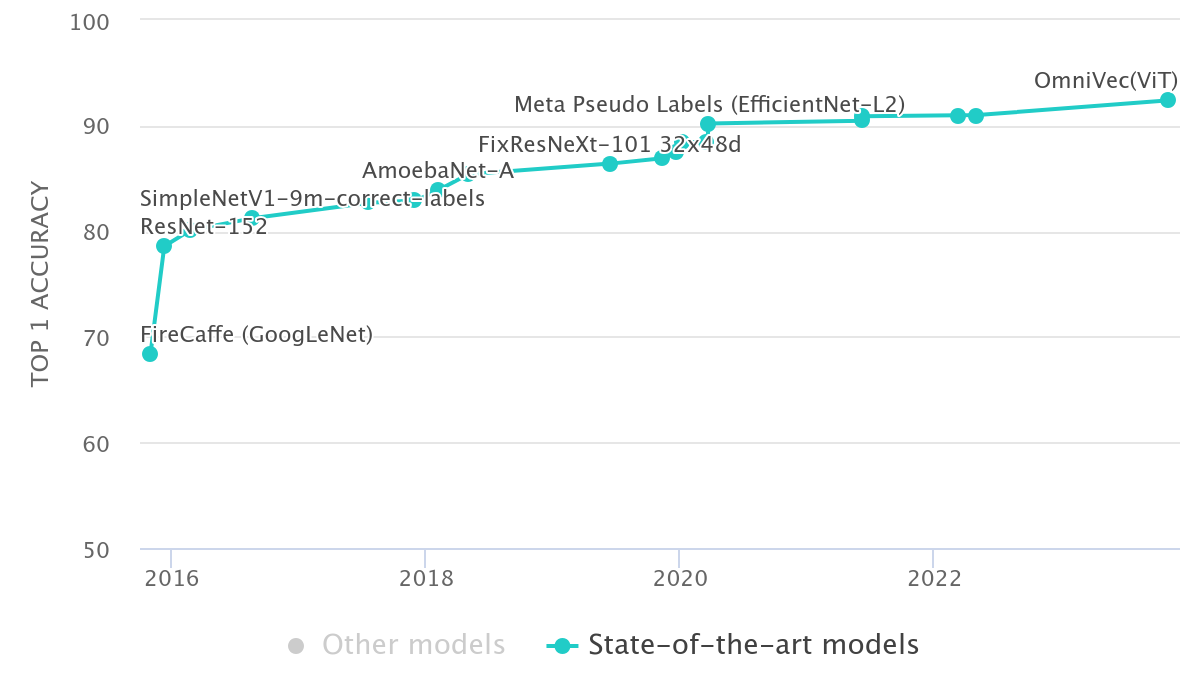
为了将Transformer引入视觉任务，Google团队开发出了Vision Transformer (ViT)，其中ViT模型以及变种在图像分类任务上一骑绝尘

ViT的结构

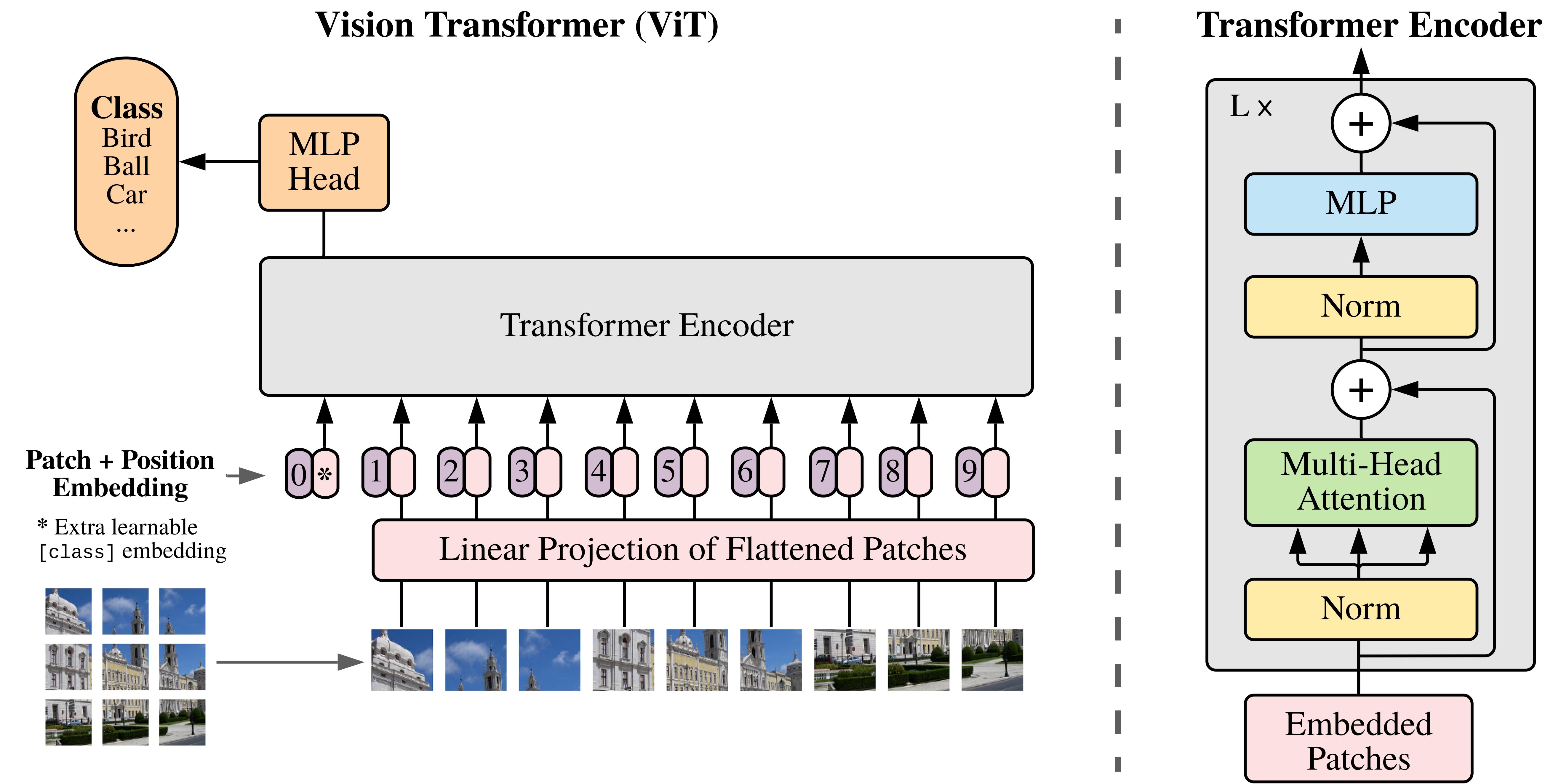
ViT首先将图像(${\mathbb{R}}^{H\times W\times C}$)划分为多个Patch($P\times P$)，Patch的维度为$P^2\times C$。可得图片划分的Patch数目为$N=\frac{HW}{P^2}$。例如输入图片大小为224x224，将图片分为固定大小的patch，patch大小为16x16，则每张图像会生成224x224/16x16=196个patch，即输入序列长度为196，每个patch维度16x16x3=768

然后使每一个Patch展平后进行线性投影为固定长度的向量。在线性投影中直接使用一个卷积核大小为16x16，步距为16，卷积核个数为768的卷积来实现。通过卷积[224, 224, 3] -> [14, 14, 768]，然后把H以及W两个维度展平即可[14, 14, 768] -> [196, 768]，此时正好变成了一个二维矩阵，正是Transformer想要的。并添加一个特殊的token[cls]与token拼接在一起以便表示为图像分类任务，此时token为的维度是197x768。到目前为止，已经通过patch embedding将一个视觉任务就转化为序列问题。

同时ViT没有采用原始Transformer的位置编码方式，而是直接设置为可学习的位置编码（Positional Encoding）。

这个过程可以公式化为：
$$\begin{array}{rlr}{\mathbf{z}}_0& =\left[\begin{array}{c}{\mathbf{x}}_{class};{\mathbf{x}}_p^1\mathbf{E};{\mathbf{x}}_p^2\mathbf{E};...;{\mathbf{x}}_p^N\mathbf{E}\end{array}\right]+{\mathbf{E}}_{pos}& \end{array}$$
表示图块编码和位置编码过程，其中$E$是线性变换矩阵且$E\in$ ${\mathbb{R}}^{(P^2\times C)\times D}$, $E_{pos}\in {\mathbb{R}}^{(N+1)\times D}$, $x_{class}$为人为增加的一个可学习的分类向量。

然后在transformer的多头注意力机制中多头自注意力时，先将输入映射到q，k，v，如果只有一个头，qkv的维度都是197x768，如果有12个头（768/12=64），则qkv的维度是197x64，一共有12组qkv，最后再将12组qkv的输出拼接起来，输出维度是197x768，然后在过一层LN，维度依然是197x768
$${\mathbf{z}}_l^{\prime }=MSA(LN({\mathbf{z}}_{l-1}))+{\mathbf{z}}_{l-1},l=1,2,..L$$
公式表示Transformer 编码器中的多头自注意力 (Multi-head Selfattention)、残差连接与层归一化 (Add &Norm) 过程，重复 L次。

紧接着使用MLP将维度放大再缩小回去
$${\mathbf{z}}_l=MLP(LN({\mathbf{z}}_l^{\prime }))+{\mathbf{z}}_l^{\prime },l=1,2,..L$$
公式表示Transformer编码器中前馈神经网络(Feed Forward Network)、残差连接与层归一化 (Add &Norm) 过程，重复 L 次。

最后使用层归一化处理
$$\mathbf{y}=LN({\mathbf{z}}_L^0)$$
一个block之后维度依然和输入相同，都是197x768，因此可以堆叠多个block。