目录
正文
1 公共密钥密码学的兴起
2 玩具版 RSA 算法
2.1 RSA 基本原理
2.2 RSA 举例说明
1 加密
2 解密
3 不是完美的陷门函数
⚠️ 原文地址:A (Relatively Easy To Understand) Primer on Elliptic Curve Cryptography
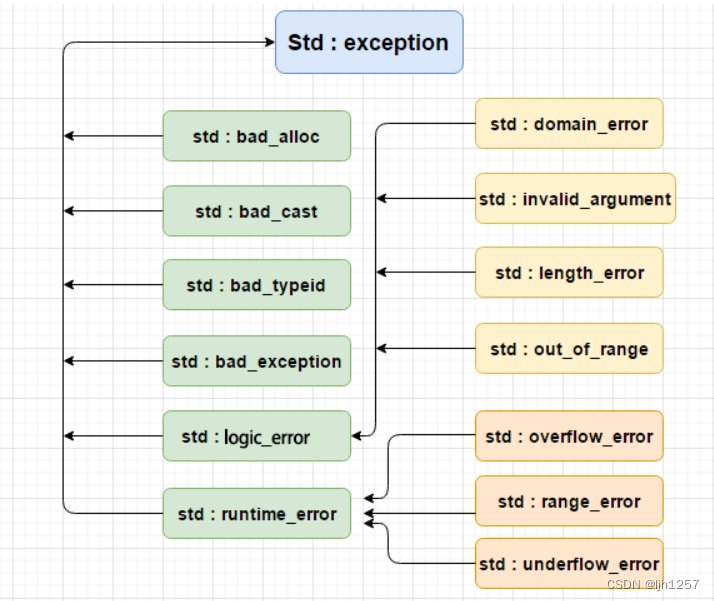
⚠️ 写在前面:本文属搬运博客,自己留着学习。如果你和我一样是小白,那么看完本文我们将仍然不能理解下图具体是在干什么,但能够对 RSA 和椭圆曲线加密的初衷有所了解。

正文
椭圆曲线密码学(ECC)是当今广泛使用但最少被理解的一种密码学类型。在 CloudFlare,我们大量使用 ECC 来保护从客户的 HTTPS 连接到我们在数据中心之间传递数据的方式。
从根本上说,我们认为能够理解任何安全系统背后的技术是信任它的关键。为此,我们在寻找一个好的、相对容易理解的 ECC 入门资料以与用户分享,但没有找到。最终,我们决定自己编写一个。以下是你要阅读的内容。
警告:这是一个复杂的话题,不可能将其浓缩成一篇精炼的博客文章。换句话说,准备好进行一次史诗般的旅程,因为有很多内容需要涵盖。如果你只想了解大意,那么长话短说:ECC 是公共密钥密码学的下一代,根据目前理解的数学,它比第一代公共密钥密码学系统如 RSA 提供了更安全的基石。如果你担心确保最高级别的安全同时保持性能,那么采用 ECC 是有意义的。如果你对细节感兴趣,请继续阅读。
1 公共密钥密码学的兴起
密码学的历史可以分为两个时代:古典时代和现代时代。这两个时代之间的分水岭出现在 1977 年,当时 RSA 算法和 Diffie-Hellman 密钥交换算法都被提出。这些新算法之所以具有革命性,是因为它们代表了首批基于数论理论的可行密码学方案;它们是首批能够在不共享秘密的情况下,在两个双方之间进行安全通信的算法。密码学从关于安全地在全球范围内运输秘密密码簿的活动,转变为了能够证明任何两个方之间通信的安全性,而无需担心有人在密钥交换过程中偷听。
本文没有介绍 Diffie-Hellman 密钥交换算法。
现代密码学的基础理念是,你可以公开你用来加密数据的密钥,而用来解密数据的密钥可以保持私密。因此,这些系统被称为公钥密码系统。
这些系统中最先出现,并且至今仍被广泛使用的是 RSA 算法,它以三位首次公开描述该算法的男性的名字首字母命名:Ron Rivest,Adi Shamir 和 Leonard Adleman 。
要让公钥密码系统工作,你需要一套易于单向处理但难以逆向的算法。在 RSA 的案例中,易于处理的算法是两个质数的乘法。如果乘法是易于的算法,那么其难以逆向的配对算法是将乘积分解为两个质数成分。具有这种特性 —— 单向容易,逆向困难 —— 的算法被称为 陷门函数。找到一个好的陷门函数对于建立一个安全的公钥密码系统至关重要。
简单来说:陷门函数中单向和逆向困难的差距越大,基于它的密码系统的安全性就越高。
2 玩具版 RSA 算法
RSA 算法是最流行且最为人理解的公钥密码系统。它的安全性依赖于 因式分解的缓慢和乘法的快速。以下是对小型 RSA 系统的工作原理的快速概述。
RSA 算法满足 “单向容易,逆向困难”,其中单向是乘法,逆向是因式分解。
2.1 RSA 基本原理
一般来说,公钥加密系统有两个组成部分,公钥和私钥。加密过程是通过将消息应用数学运算得到一个看起来随机的数字。解密过程是将这个看起来随机的数字应用不同的运算得到原始数字。用公钥进行的加密只能通过用私钥进行解密来解除。
计算机处理任意大小的数字不太合适。我们可以通过选择一个最大数,并且只处理小于最大数的数字来确保我们处理的数字不会太大。我们可以将数字看作是模拟时钟上的数字。任何结果大于最大数的计算都会被绕回到有效范围内的一个数。
由于存储空间的限制,计算机是没有办法存储一个很大的数字的原码的,因此人们引入了补码的概念,也就是对原码进行模运算。—— 计算机系统结构
在 RSA 中,这个最大值(我们称之为 max)是通过乘以两个随机质数来获得的。公钥和私钥是两个特别选择的数字,它们大于零且小于最大值,我们称它们为 pub 和 priv 。要加密一个数字,你需要将它乘以自身 pub 次,确保当你达到最大值时绕回。要解密消息,你需要将它乘以自身 priv 次,然后你就能回到原始数字。这听起来可能很惊讶,但实际上它是有效的。这一属性在被发现时是一个重大的突破。
为什么定义最大值 max?答:这个 max 实际上就是模,到时候待加密数字要对它取余。
创建 RSA 密钥对:
- 首先随机选择两个质数来获得最大值(max)。
- 然后随机选择一个数字作为公钥 pub 。
- 只要你知道这两个质数,你就可以根据这个公钥计算出相应的私钥 priv 。
这就是因式分解与破解 RSA 的关系 —— 将最大数分解为其质数成分允许你从公钥计算出某人的私钥,并解密他们的私人消息。
针对 “只要你知道这两个质数,你就可以根据这个公钥计算出相应的私钥 priv”,下文说是根据 “扩展欧几里得算法” 得到的。这又是什么算法。。。
2.2 RSA 举例说明
让我们通过一个例子来使这个概念更具体。取质数 13 和 7,它们的乘积给我们最大值 91 。让我们将公钥设置为数字 5 。然后使用我们知道 7 和 13 是 91 的因数这一事实,并应用扩展欧几里得算法这个算法,我们得到私钥是数字 29 。
这些参数(max: 91, pub: 5, priv: 29)定义了一个完全功能的 RSA 系统。你可以取一个数字,乘以自身 5 次来加密它,然后取那个数字,乘以自身 29 次,你就能得到原始数字。
让我们使用这些值来加密消息 "CLOUD" 。
1 加密
为了将消息数学化,我们必须将字母转换为数字。拉丁字母的常见表示是 UTF-8 。每个字符对应一个数字。在这种编码下,CLOUD 对应的数字是 67, 76, 79, 85, 68 。每个这些数字都小于我们的最大值 91,所以我们可以单独加密它们。让我们从第一个字母 C 开始。
我们需要将它乘以自身 5 次来得到加密值。
- 第 1 次:67(本身)
- 第 2 次:67 × 67 = 4489 = 30
- 第 3 次:30 × 67 = 2010 = 8
- 第 4 次:8 × 67 = 536 = 81
- 第 5 次:81 × 67 = 5427 = 58
这意味着 67 的加密版本是 58 。
只要乘积结果大于最大值(max),我们都需要通过除以 91 来取余数。
对于每个字母重复这个过程,我们得到加密的消息 CLOUD 变成了:
58, 20, 53, 50, 87
2 解密
为了解密这个混乱的消息,我们取每个数字并乘以自身 29 次:
- 第 1 次:58(本身)
- 第 2 次:58 × 58 = 3364 = 88
- 第 3 次:88 × 58 = 5104 = 8
- ……
- 第 29 次:9 × 58 = 522 = 67
你看看,我们又回到了 67 。这对于其他数字也有效,结果是原始消息。结论是,你可以取一个数字,乘以自身多次得到一个看起来随机的数字,然后乘以自身一个秘密的次数回到原始数字。
同样地,只要乘积结果大于最大值(max),我们都需要通过除以 91 来取余数。
3 不是完美的陷门函数
RSA 和 Diffie-Hellman 之所以强大,是因为它们伴随着严格的安全性证明。作者证明了破解系统等同于解决一个被认为难以解决的数学问题。
因式分解是一个非常著名的问题,自古以来就有人研究(参见埃拉托斯特尼筛法)。任何突破都会是重大新闻,并会给发现者带来巨大的经济利益。话说回来,因式分解在位对位的基础上并不是最困难的问题。专门算法如二次筛法和一般数域筛法被创造出来解决素数因子分解问题,并且取得了一定的成功。这些算法比简单猜测已知素数的朴素方法更快,计算强度更低。
这些因式分解算法随着被分解数字大小的增加而变得更加高效。因式分解大数字的难度与乘法大数字的难度之间的差距随着数字(即密钥的位长度)的增加而缩小。随着解密数字的计算资源的增加,需要的密钥大小必须增长得更快。这对于计算能力有限的移动和低功耗设备来说是不可持续的。因式分解和乘法之间的差距在长期内是不可持续的。
个人理解,这里的意思是:数字越大,人们所提出的因式分解算法越容易对其进行分解。在这种情况下,“因式分解的难度” 变小了,“乘法的难度” 变大了,从而二者之间的差距变小了。与此同时,RSA 算法又是一种陷门函数,二者差距的减小会导致 RSA 算法所依赖的安全性减少。
所有这些都意味着 RSA 不是密码学未来的理想系统。在理想的陷门函数中,简单方式和困难方式以相同的速率随着被讨论数字的大小变难。我们需要一个基于更好陷门函数的公钥系统。