机器学习理论入门---线性回归从理论到实践

news2025/1/19 17:20:46

线性回归是机器学习里面最简单也是最常用的算法，理解了线性回归的推导之后对于后续的学习有很大帮助，所以我决定从这里开始深入学习相关的机器学习模型。
本篇首先从矩阵求导开始切入，然后介绍一次线性回归的推导，再到代码实现。本人也是入门哈，有什么错误望轻喷。

求导

简单求导规则

首先先不管模型本身，对于机器学习来说，各种矩阵的运算非常重要，而求导又是最基础的，所以就放在最前面。（主要参考）

矩阵和标量之间的求导：形状取决于矩阵（矩阵包括向量），无论是标量对矩阵求导，矩阵对标量求导，形状都和矩阵一致，每个元素都是标量求导。

矩阵对矩阵求导：矩阵求导本质上是把向量化为标量的过程，假设存在变量 y → m × 1 \overrightarrow{y}_{m×1} y ​m×1​和对应的函数 f ( y → ) n × 1 f(\overrightarrow{y})_{n×1} f(y ​)n×1​，其中每一行为 f i ( y → ) f_{i}(\overrightarrow{y}) fi​(y ​)，此时存在求导法则：
∂ f ( y → ) ∂ y → = ( ∂ f 1 ( y → ) ∂ y 1 ⋯ ∂ f 1 ( y → ) ∂ y m ⋮ ⋱ ⋮ ∂ f n ( y → ) ∂ y 1 ⋯ ∂ f n ( y → ) ∂ y m ) n × m \frac{ \partial f(\overrightarrow{y}) }{ \partial \overrightarrow{y} }=\begin{pmatrix} \frac{ \partial f_{1}(\overrightarrow{y}) }{ \partial {y_1} } & \cdots & \frac{ \partial f_{1}(\overrightarrow{y}) }{ \partial {y_m} }\\ \vdots & \ddots & \vdots\\ \frac{ \partial f_{n}(\overrightarrow{y}) }{ \partial {y_1} } & \cdots & \frac{ \partial f_{n}(\overrightarrow{y}) }{ \partial {y_m} } \end{pmatrix}_{n×m} ∂y ​∂f(y ​)​= ​∂y1​∂f1​(y ​)​⋮∂y1​∂fn​(y ​)​​⋯⋱⋯​∂ym​∂f1​(y ​)​⋮∂ym​∂fn​(y ​)​​ ​n×m​
在矩阵运算中，由于存在行列的概念，因此需要区别两种布局方式：分子布局和分母布局：
分子布局：分子布局指的是求导后的矩阵行数和分子对应行数相等。
分母布局：分母布局指的是求导后的矩阵行数和分母对应行数相等。
显然，上面的公式为分子布局，因为分子 n n n行 ( f n × 1 ) (f_{n×1}) (fn×1​)，最终结果也是 n n n行，下面都采用分子布局计算。

下面有两个常用的偏导式，可以用于加速导数计算：
假设存在方阵 A A A和向量 y → \overrightarrow{y} y ​，

  1. ∂ A y → ∂ y → = A T \frac{ \partial A\overrightarrow{y} }{ \partial \overrightarrow{y} }=A^T ∂y ​∂Ay ​​=AT
  2. ∂ y → T A y → ∂ y → = A y → + A T y → \frac{ \partial \overrightarrow{y}^TA\overrightarrow{y} }{ \partial \overrightarrow{y} }=A\overrightarrow{y}+A^T\overrightarrow{y} ∂y ​∂y ​TAy ​​=Ay ​+ATy ​（二次型相关）,若 A A A是对称矩阵，那么可以以进一步化为 2 A y → 2A\overrightarrow{y} 2Ay ​。
    简单证明一下1：

在这里插入图片描述
这一段证明可能有点抽象，建议可以自己写一下感受一下，我简单说一下我的想法。可以看到，最后对应的每个导数，上面是 f f f，下面是 y y y，先看第一行，第一行都是对 y 1 y_1 y1​求导，从左往右分别是 f 1 f_{1} f1​到 f m f_m fm​，因此m对 y 1 y_1 y1​的求导从左往右是 ∂ f 1 ( y → ) ∂ y 1 , ∂ f 2 ( y → ) ∂ y 2 . . . , ∂ f m ( y → ) ∂ y m \frac{ \partial f_1(\overrightarrow{y}) }{ \partial {y_1} },\frac{ \partial f_2(\overrightarrow{y}) }{ \partial {y_2} }...,\frac{ \partial f_m(\overrightarrow{y}) }{ \partial {y_m} } ∂y1​∂f1​(y ​)​,∂y2​∂f2​(y ​)​...,∂ym​∂fm​(y ​)​，这其实就对应了 A A A第一列的系数，也就是 a 11 , a 21 , . . . , a m 1 a_{11},a_{21},...,a_{m1} a11​,a21​,...,am1​，相当于把列转为了行。
还有一个2我没证过，也可以尝试一下熟悉熟悉规则。

链式求导

对于一般的标量函数 f ( g ( x ) ) f(g(x)) f(g(x))，此时对于 f ( x ) f(x) f(x)和 x x x存在链式求导法则：
∂ f ( g ( x ) ) ∂ x = ∂ f ( x ) ∂ g ( x ) ∂ g ( x ) ∂ x \frac{ \partial f(g(x)) }{ \partial x }=\frac{\partial f(x)}{\partial g(x)}\frac{\partial g(x)}{\partial x} ∂x∂f(g(x))​=∂g(x)∂f(x)​∂x∂g(x)​
但是对于矩阵来说，由于矩阵的乘法一般不满足交换律，此时链式求导法则如下：
∂ f ( g ( x ) ) ∂ x = ∂ g → ∂ x → ∂ f ∂ g → \frac{ \partial f(g(x)) }{ \partial x }=\frac{\partial \overrightarrow{g}}{\partial \overrightarrow{x}}\frac{\partial f}{\partial \overrightarrow{g}} ∂x∂f(g(x))​=∂x ∂g ​​∂g ​∂f​
可以看到，大求导在后面，小求导在前面，直接面向自变量的在第一个。
下面给出一个例题，假设存在 x k + 1 = A x k + B u k x_{k+1}=Ax_k+Bu_{k} xk+1​=Axk​+Buk​，令 J = x k + 1 T x k + 1 J=x^T_{k+1}x_{k+1} J=xk+1T​xk+1​（J其实是一个控制系统里面的损失函数）,计算 ∂ J ∂ u k \frac{ \partial J }{ \partial u_{k} } ∂uk​∂J​：

在这里插入图片描述
注意其中有一步，也就是 ∂ J ∂ x k + 1 \frac{ \partial J }{ \partial x_{k+1} } ∂xk+1​∂J​，这个利用了二次型转换，相当于中间的 A A A就是单位阵 I I I， I I I是一定对称的，所以结果是 2 x k + 1 2x_{k+1} 2xk+1​。

线性回归

原理

首先是第一个模型：线性回归。可以先考虑一元线性回归，这个是最简单的回归模型，表达式为 y = w x + b y=wx+b y=wx+b，需要计算的就是两个参数： w , b w,b w,b，
用矩阵计算的相对要复杂一点（但是扩展性强），可以先考虑用标量求导的方式来证明，如下：（参考证明)
在这里插入图片描述
这个就计算到了求出导数这一步，没算出解析解，后面代码是用的梯度下降算的。
下面用矩阵的方式求解，这种方法的扩展性比较强（多元线性回归的证明也是这样，本质一样），假设 x , y x,y x,y均为 n × 1 n×1 n×1矩阵，假设结果为一列 m × 1 m×1 m×1向量 t t t，前面 m − 1 m-1 m−1个为 w w w，最后一个是 b b b，经过证明，其结果为：
t = ( x T x ) − 1 y T x t=(x^Tx)^{-1}y^Tx t=(xTx)−1yTx
下面是简单的证明，这里还是一元一次线性回归的：
在这里插入图片描述
最后的 x T y x^Ty xTy是一个 2 × 1 2×1 2×1向量，导数是 2 × 1 2×1 2×1的，分别对应 w , b w,b w,b的偏导，当偏导都为0，也就对应了最小值，所以本质还是解方程，解两个偏导方程）。有的证明会把损失函数前面加上 1 / 2 n 1/2n 1/2n,也就是除掉样本数，但本质其实是一样的，不影响求解。
我一开始其实写错了，上面打叉的就是第一次写错的，还是后面写代码的时候才发现的（所以动手实践一下还是很重要的）。
注意：损失函数本身是一个标量( 1 × 1 1×1 1×1)，其导数是 2 × 1 2×1 2×1的，对应了求解的参数矩阵。

代码

一元一次线性回归

首先是基于解方程的思路，也就是直接算出数值解（对应于上面基于矩阵的证明部分）。

def my_lr(x,y):
    n = x.shape[0]
    x = np.hstack((x,np.ones((n,1)))) # 加上一列n
    # print(x.shape) # (n,2)
    t = (inv(dot(x.T,x))@x.T@y) # t=(xx^T)^(-1)y^Tx, @表示矩阵乘法,dot也是矩阵乘法
    w,b=t[0][0],t[1][0]
    # 下面进行拟合
    y_hat = w*x[:,0]+b # 取第一列,第二列是增广的
    return y_hat

上面的本质在解方程，下面用梯度下降的思路求解：
简单概括梯度下降就是： w = w − α ▽ w=w-α▽ w=w−α▽，其中 ▽ ▽ ▽是梯度（多元情况的导数）， ▽ = ∂ J ∂ w ▽=\frac{ \partial J}{ \partial w } ▽=∂w∂J​， α α α是学习率。
首先是基于标量方式求解各个变量的，也就是用 w , b w,b w,b这样的形式写出来，然后求梯度迭代：

def my_gradi_lr(x,y):
    print('--------------基于标量的梯度下降--------------')
    # 定义损失函数:T(w,b)=1/(2m)*∑(yi_hat-yi),yi_hat=wxi-b
    # w=w-α(1/m*∑xi(yi_hat-yi)) b=b-α(1/m*∑(yi_hat-yi))
    m = x.shape[0]
    w,b=0,0
    alpha=0.01
    epochs=50
    for i in range(epochs):
        y_hat = w*x+b # 计算拟合值
        w=(w-alpha*(x.T@(y_hat-y))/m)# ∑xi(yi_hat-yi)/m
        b=(b-alpha*(np.sum(y_hat-y))/m) # ∑(yi_hat-yi)/m
        y_hat = w * x + b # 更新新y_hat计算loss
        loss = 1/(2*m)*(y_hat-y).T@(y_hat-y) # 1/(2m)*∑(yi_hat-yi)
        print('epoch:%d loss:%.4f'%(i+1,loss))
    # print(w,b)
    return w*x+b

推导的过程就是链式求导，因为是完全标量的，还是比较简单的。
下面是基于矩阵的，推导过程跟前面矩阵求解里面是一致的，如果一定要比较的话，上面那种标量直观一点，但是参数多了就不方便了，下面的适合更多参数，比如之后应该会提到的多元线性回归。

def my_mat_gradi_lr(x,y):
    print('--------------基于矩阵的梯度下降--------------')
    n = x.shape[0]
    x = np.hstack((x,np.ones((n,1)))) # 加上一列n
    alpha=0.01
    epochs=50
    t=np.zeros((2,1)) # 系数矩阵
    for i in range(epochs):
        gradi = 2*(x.T@x@t-x.T@y)/(2*n)
        t=t - alpha * gradi
        loss = (t.T@x.T@x@t+y.T@y-2*y.T@x@t)/(2*n)
        print('epoch:%d loss:%.4f' % (i + 1, loss))
    return x@t # y_hat

这两种是完全一样的，具体可以看迭代的过程，loss的变化是一模一样的。
下面是运算的结果，sklearn（sklearn model）的可以视为标答，数值解（my model）的答案是和sklearn的是一样的，说明结果是对的。两个grendient都是对应的梯度下降的解法，两种迭代的算法是一样的，从迭代过程中的loss可以看出（可以运行一下代码），由于迭代次数次数比较少（50），所以和精确解还是有一定距离。
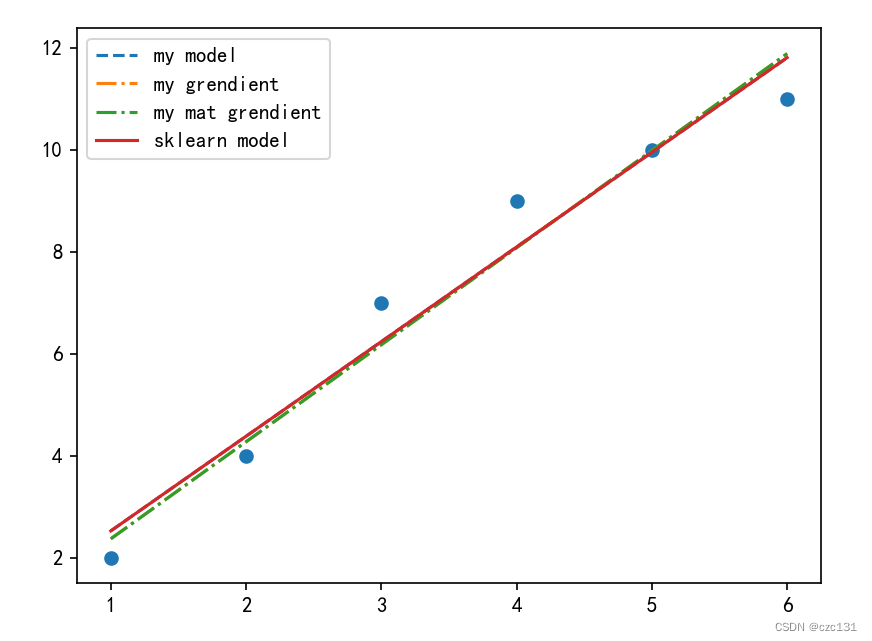
在这里插入图片描述
下面是代码：

# 一元一次线性回归

import numpy as np
from matplotlib import pyplot as plt
from numpy import dot
from numpy.linalg import inv
from sklearn.linear_model import LinearRegression
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

def my_lr(x,y):
    n = x.shape[0]
    x = np.hstack((x,np.ones((n,1)))) # 加上一列n
    # print(x.shape)
    t = (inv(dot(x.T,x))@x.T@y) # t=(xx^T)^(-1)y^Tx, @表示矩阵乘法,dot也是矩阵乘法
    # print(t.shape)
    # print(t)
    w,b=t[0][0],t[1][0]
    # print(w,b)
    # 下面进行拟合
    y_hat = w*x[:,0]+b # 取第一列,第二列是增广的
    return y_hat

def skle_lr(x,y):
    model = LinearRegression()
    model.fit(x, y)
    return model.predict(x)

# 利用梯度下降求解(基于标量链式求导)
def my_gradi_lr(x,y):
    print('--------------基于标量的梯度下降--------------')
    # 定义损失函数:T(w,b)=1/(2m)*∑(yi_hat-yi),yi_hat=wxi-b
    # w=w-α(1/m*∑xi(yi_hat-yi)) b=b-α(1/m*∑(yi_hat-yi))
    m = x.shape[0]
    w,b=0,0
    alpha=0.01
    epochs=50
    for i in range(epochs):
        # print('epoch:',i+1)
        y_hat = w*x+b # 计算拟合值
        w=(w-alpha*(x.T@(y_hat-y))/m)# ∑xi(yi_hat-yi)/m
        b=(b-alpha*(np.sum(y_hat-y))/m) # ∑(yi_hat-yi)/m
        y_hat = w * x + b # 更新新y_hat计算loss
        loss = 1/(2*m)*(y_hat-y).T@(y_hat-y) # 1/(2m)*∑(yi_hat-yi)
        print('epoch:%d loss:%.4f'%(i+1,loss))
    # print(w,b)
    return w*x+b

# 采用矩阵形式的梯度下降
def my_mat_gradi_lr(x,y):
    print('--------------基于矩阵的梯度下降--------------')
    n = x.shape[0]
    x = np.hstack((x,np.ones((n,1)))) # 加上一列n
    alpha=0.01
    epochs=50
    t=np.zeros((2,1)) # 系数矩阵
    for i in range(epochs):
        # print(x.T.shape)
        # print(t.shape)
        # print((x.T@x@t).shape)
        gradi = 2*(x.T@x@t-x.T@y)/(2*n)
        t=t - alpha * gradi
        loss = (t.T@x.T@x@t+y.T@y-2*y.T@x@t)/(2*n)
        print('epoch:%d loss:%.4f' % (i + 1, loss))
    return x@t # y_hat


if __name__ == '__main__':
    x=np.array([1,2,3,4,5,6]).reshape(-1,1)
    y=np.array([2,4,7,9,10,11]).reshape(-1,1) # 列向量
    my_y_hat = my_lr(x,y)
    skle_y_hat = skle_lr(x,y)
    my_gradi_y_hat = my_gradi_lr(x,y)
    my_mat_gradi_y_hat = my_mat_gradi_lr(x,y)
    plt.scatter(x,y)
    plt.plot(x,my_y_hat,linestyle='--',label='my model')
    plt.plot(x,my_gradi_y_hat,linestyle='-.',label='my grendient')
    plt.plot(x,my_mat_gradi_y_hat,linestyle='-.',label='my mat grendient')
    plt.plot(x,skle_y_hat,linestyle='-',label='sklearn model')
    plt.legend()
    plt.show()

多元一次线性回归

对于多元线性回归，其实本质上还是一样的，下面提供多元线性回归的代码，使用的例子是一个三元一次线性回归。具体的证明和上面矩阵证明的过程是完全一致的，解析求解的方式（求逆）的代码和一元的一样，用梯度下降方式的就改一点点就可以（其实一元也就是特殊的多元，下面这段代码也可以用）。

# 采用矩阵形式的梯度下降
def my_mat_gradi_lr(x,y):
    print('--------------基于矩阵的梯度下降--------------')
    n = x.shape[0]
    n_samples = x.shape[1]
    x = np.hstack((x,np.ones((n,1)))) # 加上一列n
    alpha=0.01
    epochs=50
    t=np.zeros((n_samples+1,1)) # 系数矩阵,唯一变化的地方
    for i in range(epochs):
        gradi = 2*(x.T@x@t-x.T@y)/(2*n)
        t=t - alpha * gradi
        loss = (t.T@x.T@x@t+y.T@y-2*y.T@x@t)/(2*n)
        print('epoch:%d loss:%.4f' % (i + 1, loss))
    return x@t # y_hat

这里因为不方便画出图像，就画出y的比较了，每个点都是实际点，线对应的都是拟合值，x轴表示第几个点。
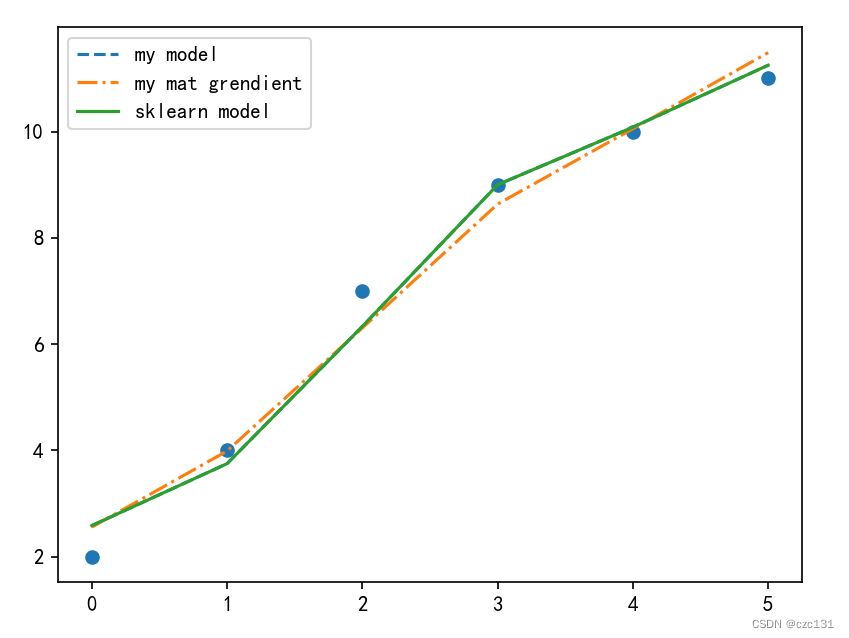
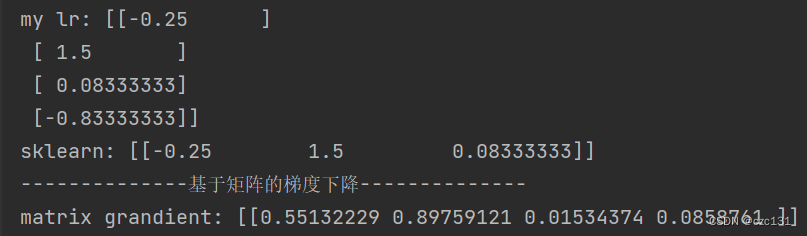
在这里插入图片描述
从结果中看解析解和sklearn得到是一样的，就是精确解，梯度下降还是差的比较多，是因为迭代次数少（50），提高到5000或者改变学习率（alpha）就可以得到更好的结果。
在这里插入图片描述
贴出代码：

# 多元线性回归
import numpy as np
from matplotlib import pyplot as plt
from numpy import dot
from numpy.linalg import inv
from sklearn.linear_model import LinearRegression

plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

def my_lr(x,y):
    n = x.shape[0]
    x = np.hstack((x,np.ones((n,1)))) # 加上一列n
    # print(x.shape)
    t = (inv(dot(x.T,x))@x.T@y) # t=(xx^T)^(-1)y^Tx, @表示矩阵乘法,dot也是矩阵乘法
    # 下面进行拟合
    print('my lr:',t)
    return x@t


def skle_lr(x,y):
    model = LinearRegression()
    model.fit(x, y)
    print('sklearn:',model.coef_)
    return model.predict(x)


# 采用矩阵形式的梯度下降
def my_mat_gradi_lr(x,y):
    print('--------------基于矩阵的梯度下降--------------')
    n = x.shape[0]
    n_samples = x.shape[1]
    x = np.hstack((x,np.ones((n,1)))) # 加上一列n
    alpha=0.01
    epochs=50
    t=np.zeros((n_samples+1,1)) # 系数矩阵
    for i in range(epochs):
        gradi = 2*(x.T@x@t-x.T@y)/(2*n)
        t=t - alpha * gradi
        loss = (t.T@x.T@x@t+y.T@y-2*y.T@x@t)/(2*n)
        # print('epoch:%d loss:%.4f' % (i + 1, loss))
    print('matrix grandient:',t.T)
    return x@t # y_hat


if __name__ == '__main__':
    x=np.array([[1,2,3,4,5,6],[2,3,5,7,8,9],[8,7,5,4,2,1]]).T
    y=np.array([2,4,7,9,10,11]).reshape(-1,1) # 列向量
    my_y_hat = my_lr(x,y)
    skle_y_hat = skle_lr(x,y)
    my_mat_gradi_y_hat = my_mat_gradi_lr(x,y)
    plot_x = np.arange(y.shape[0])
    plt.scatter(plot_x,y)
    plt.plot(plot_x,my_y_hat,linestyle='--',label='my model')
    plt.plot(plot_x,my_mat_gradi_y_hat,linestyle='-.',label='my mat grendient')
    plt.plot(plot_x,skle_y_hat,linestyle='-',label='sklearn model')
    plt.legend()
    plt.show()

❀❀❀完结撒花❀❀❀

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1602814.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

2024第十五届蓝桥杯JavaB组省赛部分题目

2024第十五届蓝桥杯JavaB组省赛部分题目

目录 第三题 第四题 第五题 第六题 第七题 第八题 转载请声明出处，谢谢！ 填空题暂时可以移步另一篇文章：2024第十五届蓝桥杯 Java B组 填空题-CSDN博客 第三题 第四题 第五题 第六题 第七题 第八题 制作不易，还请点个赞支持…
阅读更多...
PyTorch深度学习之旅：从入门到精通的十个关键步骤

PyTorch深度学习之旅：从入门到精通的十个关键步骤

在人工智能的浪潮中，深度学习框架扮演着至关重要的角色。PyTorch作为其中的佼佼者，以其简洁、直观和灵活的特性，吸引了众多开发者与研究者。本文将引导您逐步掌握PyTorch，从基础概念到高级应用，让您在深度学习的道路上…
阅读更多...
LLM推理框架Triton Inference Server学习笔记(二): Triton模型部署流程(stey by stey)

LLM推理框架Triton Inference Server学习笔记(二): Triton模型部署流程(stey by stey)

官方文档查阅: TritonInferenceServer文档 1. 写在前面 上一篇文章对triton inference server进行了一个整体的介绍，解答了三个经典问题what, why, how。 这篇文章就开始转入实践， 从实践的角度整理Triton模型部署的全流程， 如果我有一个训…
阅读更多...
一篇文章带你快速认识边缘计算（必看）

一篇文章带你快速认识边缘计算（必看）

引言 5G时代带来了万物互联的飞跃，但随之而来的是数据量爆炸性增长与集中式数据中心处理模式的瓶颈：响应延迟、带宽压力、安全隐忧。边缘计算应运而生，借鉴生物智能分布式原理，将计算与分析推向数据源头，有效解决了以上…
阅读更多...
Promise模块化编程ES6新特性

Promise模块化编程ES6新特性

文章目录 Promise&模块化编程1.Promise基本介绍2.快速入门1.需求分析2.原生ajax jQuery3.Promise使用模板 3.课后练习1.原生ajax jQuery2.promise 4.模块化编程基本介绍5.CommonJS基本介绍6.ES5模块化编程1.题目2.示意图3.代码实例—普通导入导出function.jsuse.js 4.代码…
阅读更多...
一文搞懂Kotlin符号处理接口KSP

一文搞懂Kotlin符号处理接口KSP

公众号「稀有猿诉」 原文链接 一文搞懂Kotlin符号处理接口KSP Kotlin符号处理（Kotlin Symbol Processing）即KSP是可以用于开发轻量级编译器插件的一套API。是Kotlin原生的，Kotlin语法友好的编译器插件。使用简单且易于上手&#xff0c…
阅读更多...
同城货运系统的开发与货运搬家软件的技术性探讨和市场分析

同城货运系统的开发与货运搬家软件的技术性探讨和市场分析

一、市场前景展望 随着城市化进程的加快和电商物流的蓬勃发展，同城货运市场展现出了巨大的潜力。尤其是在快节奏的生活环境中，个人和企业对于快速、便捷、可靠的货运搬家服务需求日益增长。同城货运系统与货运搬家软件作为连接货主与货运司机的桥梁&…
阅读更多...
2024还想走c++后端的同学，该如何准备才有机会成功上岸拿到offer

2024还想走c++后端的同学，该如何准备才有机会成功上岸拿到offer

c后端，一个被网上说没有市场的c方向。但是对于想从事c后端的同学该如何准备呢？ 就目前的市场需求来说，c后端的需求市真不大，中小厂基本没有，大部分集中在大厂。 那么，如果大家想求职c后端，第一…
阅读更多...
野生动物保护视频AI智能监管方案，撑起智能保护伞，守护野生动物

野生动物保护视频AI智能监管方案，撑起智能保护伞，守护野生动物

一、背景 在当今世界，野生动物保护已经成为全球性的重要议题。然而，由于野生动物生存环境的不断恶化以及非法狩猎等活动的盛行，保护野生动物变得尤为迫切。为了更有效地保护野生动物，利用视频智能监管技术成为一种可行的方案。 …
阅读更多...
docker方式 部署jenkins服务，实现持续集成（CI/CD）功能

docker方式 部署jenkins服务，实现持续集成（CI/CD）功能

一、背景： 因公司需求，需要部署一套jenkins自动化部署服务，并且是通过docker容器的方式部署的。 二、jenkins简介： 什么是Jenkins ？ Jenkins是一个开源软件，是基于Java开发的一种持续集成工具，用…
阅读更多...
VS集成vcpkg

VS集成vcpkg

VS集成vcpkg 下载vcpkg 下载vcpkg git clone https://github.com/Microsoft/vcpkg.git安装vcpgk，文件目录 .\bootstrap-vcpkg.bat集成到vs2022中 # 集成到项目 vcpkg integrate project vcpkg integrate installPS C:\Users\Administrator> vcpkg integrate…
阅读更多...
Python入门教程完整版（懂中文就能学会）

Python入门教程完整版（懂中文就能学会）

网友虐我千百遍，我待网友如初恋，因为今天又给大家带来了干货，Python入门教程完整版，完整版啊！完整版！ 为了吸取教训，小编一定要分享一下攻略，“怎样获得小编分享的教程呢&#xff1…
阅读更多...
多线程同步：使用 std::mutex 和 std::unique_lock 保护共享资源

多线程同步：使用 std::mutex 和 std::unique_lock 保护共享资源

在当今的软件开发中，多线程编程是一项至关重要的技术，它允许程序同时执行多个任务，从而提高应用程序的效率和响应速度。然而，多线程环境也带来了数据安全和一致性的挑战。在多个线程需要访问和修改同一数据资源的情况下&#xff0…
阅读更多...
【SAP NWDI】创建DC（Development component）（三）

【SAP NWDI】创建DC（Development component）（三）

一、准备DC组件包 首先需要下载下面这7个sca 的组件包，找到对应的ME版本的组件包，可以找对应的Basis帮忙下载。然后把这7个组件包放入到服务器中根目录的这个目录中，如果目录没有的需要自己创建出来。 二、导入DC组件包 注意：下面的的图中 有需要填写 in 和 out 的连个目…
阅读更多...
RabbitMQ-核心特性

RabbitMQ-核心特性

已经不需要为RabbitMQ交换机的离去而感到伤心了，接下来登场的是RabbitMQ-核心特性!!! 文章目录 核心特性消息过期机制消息确认机制死信队列 核心特性 消息过期机制 官方文档：https://www.rabbitmq.com/ttl.html 可以给每条消息指定一个有效期&#xf…
阅读更多...
富文本在线编辑器 - tinymce

富文本在线编辑器 - tinymce

tinymce 项目是一个比较好的富文本编辑器. 这里有个小demo, 下载下来尝试一下, 需要配置个本地服务器才能够访问, 我这里使用的nginx, 下面是我的整个操作过程: git clone gitgitee.com:chick1993/layui-tinymce.git cd layui-tinymcewget http://nginx.org/download/nginx-1.…
阅读更多...
监控系统泛滥：CTO 面临的隐形成本危机

监控系统泛滥：CTO 面临的隐形成本危机

在信息技术飞速发展的今天，构建和维护现代化的数字系统变得日益复杂和关键；在这样的背景下，监控系统的作用变得尤为突出。正如业界广泛流传的一句经验之谈“无监控，不运维”所揭示的道理一样，对于任何具有一定复杂性的…
阅读更多...
Redis（Windows版本下载安装和使用）

Redis（Windows版本下载安装和使用）

天行健，君子以自强不息；地势坤，君子以厚德载物。 每个人都有惰性，但不断学习是好好生活的根本，共勉！ 文章均为学习整理笔记，分享记录为主，如有错误请指正，共同学习进步。…
阅读更多...
lua 光速入门

lua 光速入门

文章目录 安装注释字符串变量逻辑运算条件判断循环函数Table (表)常用全局函数模块化 首先明确 lua 和 js Python一样是动态解释性语言，需要解释器执行。并且不同于 Python 的强类型与 js 的弱类型，它有点居中，倾向于强类型。 安装 下载解释…
阅读更多...
AI预测福彩3D第38弹【2024年4月17日预测--第8套算法开始计算第6次测试】

AI预测福彩3D第38弹【2024年4月17日预测--第8套算法开始计算第6次测试】

今天咱们继续测试第8套算法和模型，今天是第5次测试，目前的测试只是为了记录和验证，为后续的模型修改和参数调整做铺垫，所以暂时不建议大家盲目跟买~废话不多说了，直接上结果！ 2024年4月17日3D的七码预测结果…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023