备战2024年蓝桥杯 -- 每日一题
Python大学A组
试题一:公约数
试题二:最大公约数
试题三:等差数列
试题四:最大比例
试题五:Hankson的趣味题
试题一:公约数
【题目描述】
给定两个正整数 a 和 b。你需要回答 q 个询问。每个询问给定两个整数 l,r,你需要找到最大的整数 x,满足:
- x 是 a 和 b 的公约数。
- l≤x≤r。
【输入格式】
第一行包含两个整数 a,b。
第二行包含一个整数 q。
接下来 q 行,每行包含两个整数 l,r。
【输出格式】
每个询问输出一行答案,即满足条件的最大的 x,如果询问无解,则输出 −1。
【数据范围】
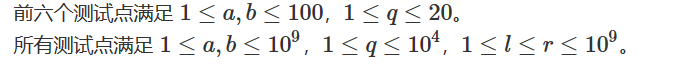
【输入样例】
9 27
3
1 5
10 11
9 11【输出样例】
3
-1
9【解题思路】
a和b的公约数一定是a,b最大公因数的约数。所以直接枚举出gcd(a,b)的所有约数,然后找l,r范围内的最大的一个。
【Python程序代码】
from math import *
a,b = map(int,input().split())
ca,cb = [],[]
i = 1
while i*i<=a:
if a%i==0:
ca.append(i)
if a//i !=i:ca.append(a//i)
i += 1
i = 1
while i*i<=b:
if b%i==0:
cb.append(i)
if b//i !=i:cb.append(b//i)
i += 1
ca.sort(); cb.sort()
con = []
for i in ca:
if i in cb:con.append(i)
con.sort()
q = int(input())
#print(con)
for _ in range(q):
a,b = map(int,input().split())
l,r = 0,len(con)-1
while l<r:
mid = (l+r)>>1
if con[mid]>=a:r=mid
else:l=mid+1
ll,rr=0,len(con)-1
while ll<rr:
mid = (ll+rr+1)>>1
if con[mid]<=b:ll=mid
else:rr=mid-1
#print("r = %d rr = %d"%(r,rr))
if con[r]>=a and con[rr]<=b:
if con[r]<=b and con[rr]>=a:
print(max(con[r],con[rr]))
elif con[r]<=b and con[rr]<a:
print(con[r])
elif con[r]>b and con[rr]>=a:
print(con[rr])
else:
print(-1)
else:
print(-1)
试题二:最大公约数
【题目描述】
给定 n对正整数 ai,bi,请你求出每对数的最大公约数。
【输入格式】
第一行包含整数 n。
接下来 n行,每行包含一个整数对 ai,bi。
【输出格式】
输出共 n 行,每行输出一个整数对的最大公约数。
【数据范围】
1≤n≤105,
1≤ai,bi≤2×109
【输入样例】
2
3 6
4 6【输出样例】
3
2【解题思路】
模板题
【Python程序代码】
from math import *
def gcd1(a,b):
if b==0:return a
return gcd1(b,a%b)
n = int(input())
for i in range(n):
a,b = map(int,input().split())
print(gcd(a,b))试题三:等差数列
【题目描述】
数学老师给小明出了一道等差数列求和的题目。但是粗心的小明忘记了一部分的数列,只记得其中 N 个整数。现在给出这 N 个整数,小明想知道包含这 N 个整数的最短的等差数列有几项?
【输入格式】
输入的第一行包含一个整数 N。
第二行包含 N 个整数 A1,A2,⋅⋅⋅,AN。(注意 A1∼AN 并不一定是按等差数列中的顺序给出)
【输入格式】
输出一个整数表示答案。
【数据范围】
2≤N≤100000
0≤Ai≤109
【输入样例】
5
2 6 4 10 20【输出样例】
10【解题思路】
排序后,求出相邻数差的最大公约数
【Python程序代码】
from math import *
n = int(input())
a = list(map(int, input().split()))
a.sort()
d = a[1]-a[0]
if d==0:
print(len(a))
else:
for i in range(1,n):
d = min(d,gcd(a[i]-a[i-1],d))
print( (a[-1]-a[0])//d+1 )试题四:最大比例
【题目描述】
X星球的某个大奖赛设了 M 级奖励。每个级别的奖金是一个正整数。并且,相邻的两个级别间的比例是个固定值。也就是说:所有级别的奖金数构成了一个等比数列。比如:16,24,36,54,其等比值为:3/2。现在,我们随机调查了一些获奖者的奖金数。请你据此推算可能的最大的等比值。
【输入格式】
第一行为数字 N ,表示接下的一行包含 N 个正整数。
第二行 N 个正整数 Xi,用空格分开,每个整数表示调查到的某人的奖金数额。
【输出格式】
一个形如 A/B 的分数,要求 A、B 互质,表示可能的最大比例系数。
【输入样例】
3
1250 200 32【输出样例】
25/4【解题思路】
先排个序,然后分子分母分别除以a[0],b[0]。然后分子分母序列进行辗转相减法,由于是指数上的运算应写成除法。
【Python程序代码】
from math import *
n = int(input())
s = list(map(int,input().split()))
s = list(set(s))
s.sort()
a,b = [],[]
for i in range(1,len(s)):
co = gcd(s[i],s[0])
a.append(s[i]//co)
b.append(s[0]//co)
up,down = a[0],b[0]
def gcd_sub(a,b):
if a<b:a,b=b,a
if b==1:return a
return gcd_sub(b,a//b)
for i in range(1,len(a)):
up = gcd_sub(up,a[i])
down = gcd_sub(down,b[i])
print("%d/%d"%(up,down))
试题五:Hankson的趣味题
【题目描述】
Hanks 博士是 BT(Bio-Tech,生物技术)领域的知名专家,他的儿子名叫 Hankson。现在,刚刚放学回家的 Hankson 正在思考一个有趣的问题。今天在课堂上,老师讲解了如何求两个正整数 c1 和 c2的最大公约数和最小公倍数。现在 Hankson 认为自己已经熟练地掌握了这些知识,他开始思考一个“求公约数”和“求公倍数”之类问题的“逆问题”,这个问题是这样的:已知正整数 a0,a1,b0,b1,设某未知正整数 x 满足:
- x 和 a0的最大公约数是 a1;
- x 和 b0的最小公倍数是 b1。
Hankson 的“逆问题”就是求出满足条件的正整数 x。但稍加思索之后,他发现这样的 x 并不唯一,甚至可能不存在。因此他转而开始考虑如何求解满足条件的 x 的个数。请你帮助他编程求解这个问题。
【输入格式】
输入第一行为一个正整数 n,表示有 n 组输入数据。
接下来的 n 行每行一组输入数据,为四个正整数 a0,a1,b0,b1,每两个整数之间用一个空格隔开。
输入数据保证 a0能被 a1 整除,b1 能被 b0 整除。
【数据范围】
1≤n≤2000,
1≤a0,a1,b0,b1≤2∗109
【输入样例】
2
41 1 96 288
95 1 37 1776【输出样例】
6
2【解题思路】
首先x一定是b1的约数,所以直接枚举b1的约数,判断是否满足那两个条件。
【Python程序代码】
from math import *
import sys
input = sys.stdin.readline
n = int(input())
for i in range(n):
a0,a1,b0,b1 = map(int,input().split())
tep = []
i = 1
while i*i<=b1:
if b1%i==0:
tep.append(i)
if b1//i!=i:tep.append(b1//i)
i += 1
res = 0
for x in tep:
if gcd(x,a0)==a1 and x*b0//gcd(x,b0)==b1:res+=1
print(res)