Map与Set的模拟实现封装

news2024/11/24 14:37:44

目录

一.   底层原理

 二.   红黑树节点的定义

三.   仿函数封装

四.   基本函数的封装

五.   迭代器的封装

5.1   迭代器的基本定义

5.2   *与->操作

5.3  迭代器的++操作

5.3.1   右子树不为空

5.3.2   右子树为空 

5.4   迭代器的--操作

5.4.1   当前节点的父节点为空

 5.4.2   左子树不为空

5.4.3   左子树为空

5.5   ==与！=操作

六.   Map整体封装

七.   Set整体封装

八.   红黑树整体封装

一.   底层原理

        我们需要知道的是Map和Set底层是由红黑树封装的。而我们红黑树的底层又是kv结构。那我们可以把红黑树的V变成Map和Set传参的地方，Map传的是Key，Set传的是pair<Key,value>。

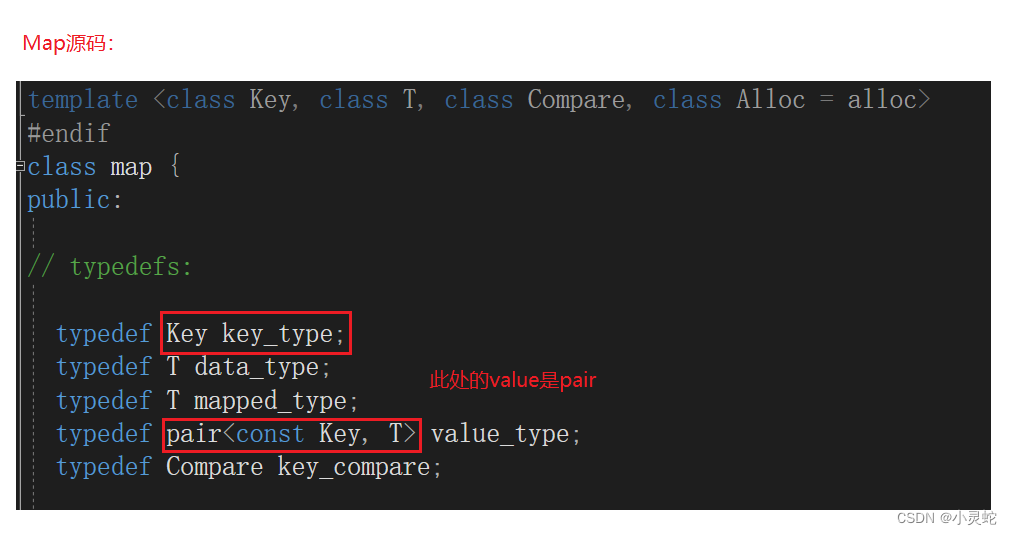
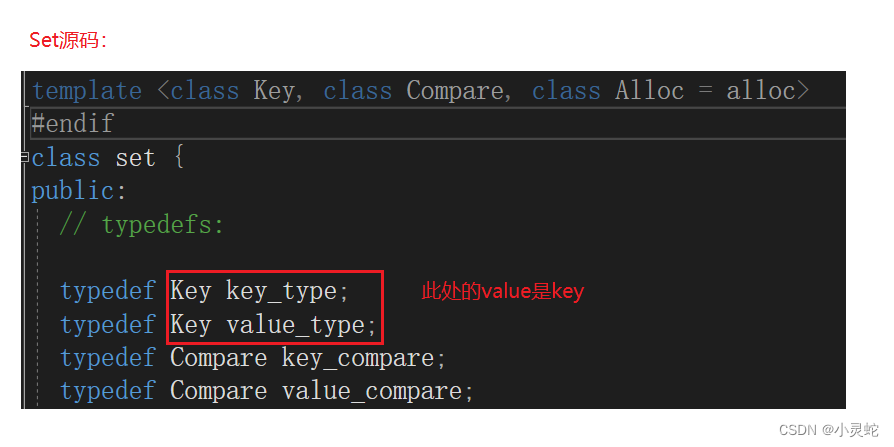
因此我们可以为了识别到底是Map还是Set定义一个模板参数T。

template<class K,class T>
class RBTree{};

此处参数K依旧是Key，只不过参数T可以是Set的Key，也可以是Map的pair<Key,Value>。

如果是Map，那么传参就是：

template<class K,class T>
class Map
{
private:
	RBTree<K, pair<K,T>> _map;
};

而如果是Set，那么传参就是：

template<class K>
class Set
{
private:
	RBTree<K,K> _set;
};

我们可以看见，无论是Map还是Set，好像T参数已经包含了K参数，那为什么还要第一个参数K参数呢？

因为我们除了去insert(const Value& v)以外，还有find(const Key& k)操作，而find函数就需要第一个参数K，而如果不要第一个参数Set是不能满足的，所以第一个参数是必需的。

 二.   红黑树节点的定义

这里节点的定义我们与前面普通的红黑树(具体的定义可看：http://t.csdnimg.cn/hlYqJ)不一样的是，我们需要去考虑到底是Map还是Set，也就是传的参数不一样。所以可以用一个模板参数来定义：

enum Colour
{
	RED,
	BLACK
};
template<class T>
struct RBTreeNode
{
	RBTreeNode<T>* _left;
	RBTreeNode<T>* _right;
	RBTreeNode<T>* _parent;
	Colour _col;
	T _data;
	RBTreeNode(const T& data)
		:_left(nullptr)
		,_right(nullptr)
		,_parent(nullptr)
		,_col(RED)
		,_data(data)
	{}
};

此处T，Map就传pair<Key,Value>，而Set就传Key。

三.   仿函数封装

我们可以看见对于Map的pair我们是不能做比较，也做不了比较的，但是我们可以知道的是Key是能做比较的，因此我们需要将pair中的Key取出来作比较，这里就能用到我们的仿函数。

仿函数(functor)是一种在C++中使用的概念，它允许一个类的对象表现得像函数一样。仿函数通过在其类定义中重载函数调用运算符operator()来实现这种行为。

  • 对于Map我们需要取出pair键值对中的第一个元素Key。
namespace yjy {
	template<class K,class T>
	class Map
	{
		struct MapKeyOfT
		{
			const K& operator()(const pair<K,T>& kt)
			{
				return kt.first;
			}
		};
	private:
		RBTree<K, pair<K,T>, MapKeyOfT> _map;
	};
}
  • 对于Set我们直接返回自带的Key就行。
namespace yjy {
	template<class K>
	class Set
	{
		struct SetKeyOfT
		{
			const K& operator()(const K& key)
			{
				return key;
			}
		};
	private:
		RBTree<K,K, SetKeyOfT> _set;
	};
}

 整体的仿函数传参即：

 那么有了我们的仿函数之后，我们就可以运用在下面这样的比较之中：

bool Find(const T& data)
{
	KeyOfT _rot;
	Node* cur = _root;
	while (cur)
	{
		if (_rot(cur->_data) < _rot(data))
		{
			cur = cur->_right;
		}
		else if (_rot(cur->_data) > _rot(data))
		{
			cur = cur->_left;
		}
		else
		{
			return true;
		}
	}
	return false;
}

四.   基本函数的封装

我们有了仿函数之后，就可以对一些基本操作函数进行编写(此处只是在红黑树的基础上加上了仿函数，如果对操作还有不懂的，可以去看：http://t.csdnimg.cn/577bU)。

bool Find(const T& data)
{
	KeyOfT _rot;
	Node* cur = _root;
	while (cur)
	{
		if (_rot(cur->_data) < _rot(data))
		{
			cur = cur->_right;
		}
		else if (_rot(cur->_data) > _rot(data))
		{
			cur = cur->_left;
		}
		else
		{
			return true;
		}
	}
	return false;
}
bool Insert(const T& data)
{
	if (_root == nullptr)
	{
		_root = new Node(data);
		_root->_col = BLACK;
		return true;
	}
	KeyOfT _rot;
	Node* parent = nullptr;
	Node* cur = _root;
	while (cur)
	{
		if (_rot(cur->_data) > _rot(data))
		{
			parent = cur;
			cur = cur->_left;
		}
		else if (_rot(cur->_data) < _rot(data))
		{
			parent = cur;
			cur = cur->_right;
		}
		else
		{
			return true;
		}
	}
	cur = new Node(data);
	Node* newnode = cur;
	if (_rot(parent->_data) < _rot(data))
	{
		parent->_right = cur;
	}
	else
	{
		parent->_left = cur;
	}
	cur->_parent = parent;
	while (parent && parent->_col == RED)
	{
		Node* grandparent = parent->_parent;
		Node* uncle = nullptr;
		//parent和uncle是grandparent的左还是右不影响结果
		//cur是parent的左还是右不影响结果
		if (parent == grandparent->_left)
		{
			uncle = grandparent->_right;
			//uncle存在且为红
			if (uncle && uncle->_col == RED)
			{
				parent->_col = BLACK;
				uncle->_col = BLACK;
				grandparent->_col = RED;
				if (grandparent == _root)
				{
					grandparent->_col = BLACK;
				}
				else
				{
					cur = grandparent;
					parent = cur->_parent;
				}
			}
			else
			{
				//		g
				//	p		u
				//c
				if (cur == parent->_left)
				{
					RotaleR(grandparent);
					parent->_col = BLACK;
					grandparent->_col = RED;
				}
				//		g
				//	p		u
				//		c
				else
				{
					RotaleL(parent);
					RotaleR(grandparent);
					cur->_col = BLACK;
					grandparent->_col = RED;
				}
				break;
			}
		}
		else
		{
			uncle = grandparent->_left;
			if (uncle && uncle->_col == RED)
			{
				parent->_col = BLACK;
				uncle->_col = BLACK;
				grandparent->_col = RED;
				if (grandparent == _root)
				{
					grandparent->_col = BLACK;
				}
				else
				{
					cur = grandparent;
					parent = cur->_parent;
				}
			}
			else
			{
				//		g
				//	u		p
				//				c
				if (cur == parent->_right)
				{
					RotaleL(grandparent);
					parent->_col = BLACK;
					grandparent->_col = RED;
				}
				//		g
				//	u		p
				//		c
				else
				{
					RotaleR(parent);
					RotaleL(grandparent);
					cur->_col = BLACK;
					grandparent->_col = RED;
				}
				break;
			}
		}
	}
	return true;
}
void RotaleL(Node* parent)
{
	Node* subR = parent->_right;
	Node* subRL = subR->_left;
	parent->_right = subRL;
	subR->_left = parent;
	if (subRL)
	{
		subRL->_parent = parent;
	}
	Node* ppnode = parent->_parent;
	parent->_parent = subR;
	if (parent == _root)
	{
		_root = subR;
		subR->_parent = nullptr;
	}
	else
	{
		if (parent == ppnode->_left)
		{
			ppnode->_left = subR;
		}
		else if (parent == ppnode->_right)
		{
			ppnode->_right = subR;
		}
		subR->_parent = ppnode;
	}
}
void RotaleR(Node* parent)
{
	Node* subL = parent->_left;
	Node* subLR = subL->_right;
	parent->_left = subLR;
	subL->_right = parent;
	if (subLR)
	{
		subLR->_parent = parent;
	}
	Node* ppnode = parent->_parent;
	parent->_parent = subL;
	if (parent == _root)
	{
		_root = subL;
		subL->_parent = nullptr;
	}
	else
	{
		if (ppnode->_left == parent)
		{
			ppnode->_left = subL;
		}
		else if (ppnode->_right == parent)
		{
			ppnode->_right = subL;
		}
		subL->_parent = ppnode;
	}
}

五.   迭代器的封装

我们写出了仿函数之后，一切都水到渠成了，就可以继续对迭代器进行封装了。

5.1   迭代器的基本定义

template<class T,class Ptr,class Ref>//此处Ptr是T*，Ref是T&
struct RBTreeIterator
{
	typedef RBTreeNode<T> Node;
	typedef RBTreeIterator<T,Ptr,Ref> Self;
	Node* _node;
	RBTreeIterator(Node* node)
		:_node(node)
	{}
}

5.2   *与->操作

对于*操作，就是返回数据的引用，而->操作，就是返回数据的地址，即指针。

Ref operator*()
{
	return _node->_data;
}
Ptr operator->()
{
	return &_node->_data;
}

5.3  迭代器的++操作

此处我们需要分为右子树不为空和右子树为空两种情况。为什么呢？

我们可以根据二叉树的中序遍历来看，根节点遍历完了，就该遍历右子树，如果右子树为空，则直接跳到上一层，如果不为空，则进入右子树。那么我们下面来细讲一下这两种情况。 

Self& operator++()
{
	if (_node->_right)//右边不为空
	{
		//右子树的最左边节点
		Node* subright = _node->_right;
		while (subright->_left)
		{
			subright = subright->_left;
		}
		_node = subright;
	}
	else
	{
		//祖先里面孩子是父亲左的那个
		Node* cur = _node;
		Node* subparent = _node->_parent;
		while (subparent&&subparent->_right == cur)
		{
			cur = subparent;
			subparent = subparent->_parent;
		}
		_node = subparent;
	}
	return *this;
}

5.3.1   右子树不为空

 我们可以根据中序来解释，进入右子树之后，我们应该进入右子树的最左节点。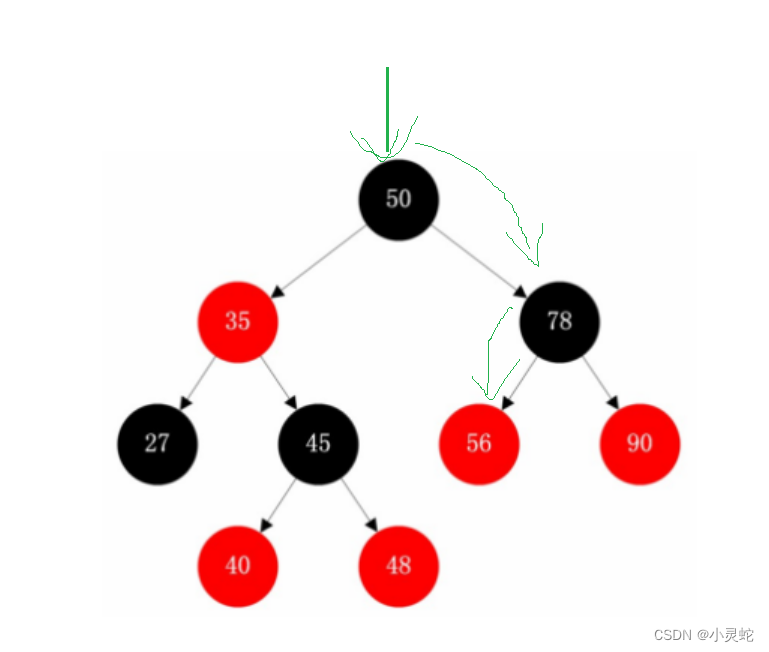

 如图，当前节点是50，右子树不为空，则走到右子树的最左节点56。

5.3.2   右子树为空 

当右子树为空的情况出现时，我们可以知道后面一步需要遍历到当前节点的父节点，那么我们再进一步思考一下，当前节点是父节点的右节点时，又说明父节点的右子树遍历完了，又需要向上迭代。所以我们要迭代到什么时候才行呢？

应该是迭代到当前节点是父节点的左节点时，此时后面一步就是到父节点。

如图：当前节点是48，右节点为空，则向上走，一直走到35的时候，此时35是50的左节点。 

5.4   迭代器的--操作

--操作与++操作不同，不只是迭代的方向不同，情况也有所不同。

我们这里要先判断当前节点的父节点是否为空节点。为什么呢？咱们下面再说。除了这种情况外，还有左子树不为空和左子树为空两种情况。

Self& operator--()
{
	if (_node->_parent==nullptr)
	{
		Node* maxright = _node;
		while (maxright->_right)
		{
			maxright = maxright->_right;
		}
		_node = maxright;
	}
	else if (_node->_left)//左边不为空
	{
		//左子树的最右边节点
		Node* subright = _node->_left;
		while (subright->_right)
		{
			subright = subright->_right;
		}
		_node = subright;
	}
	else
	{
		//祖先里面孩子是父亲右的那个
		Node* cur = _node;
		Node* subparent = _node->_parent;
		while (subparent && subparent->_left == cur)
		{
			cur = subparent;
			subparent = subparent->_parent;
		}
		_node = subparent;
	}
	return *this;
}

5.4.1   当前节点的父节点为空

当前节点的父节点为空，证明当前节点是此时的根节点。我们再进行--的话，就要走到最右边节点。因为在STL库定义中，是如下图一样的结构：

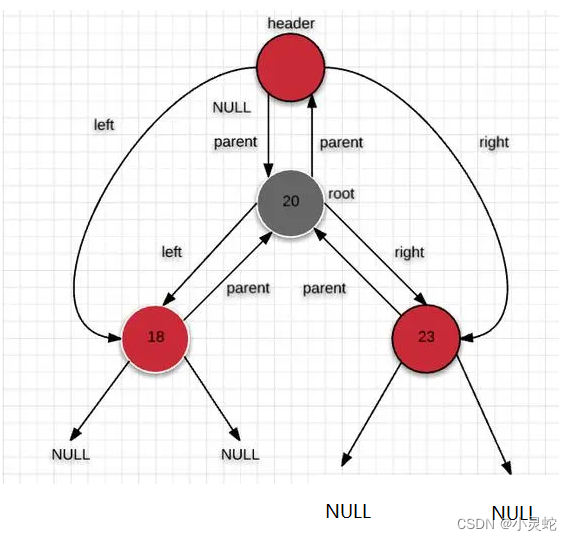
我们这里就没有定义header头结点，但是我们还是可以看到，根节点之后应该到最右节点。

 5.4.2   左子树不为空

此时根据++操作右子树不为空时的情况可以得到此时应该走到左子树的最右节点。

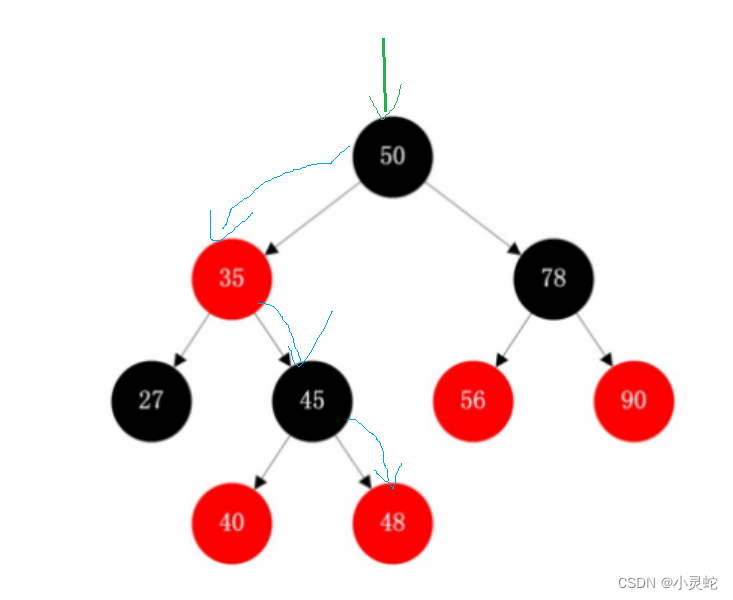
如图：当前节点是50，此后应该迭代到左子树的最右节点，即48。 

5.4.3   左子树为空

此时也应该向上迭代，到什么时候结束呢？

应该到当前节点是父节点的右节点为止，因为如果当前节点是父节点的左节点时，又说明左子树走完了，又要向上迭代。所以我们要一直迭代到当前节点是父节点的右节点时。

 

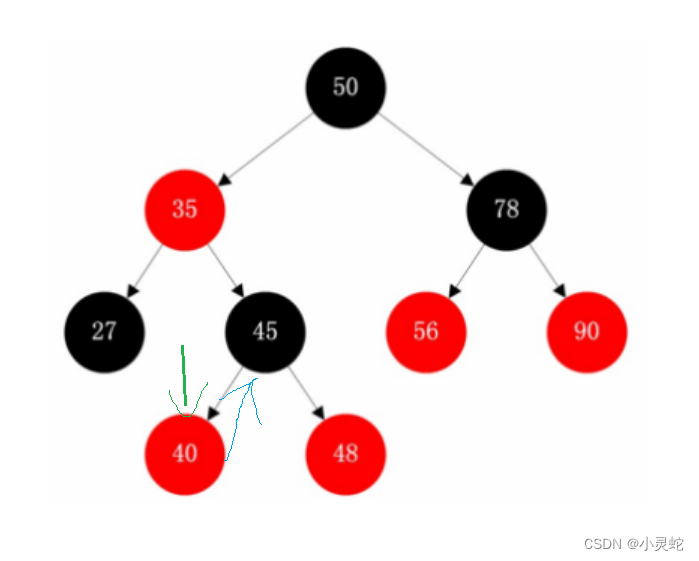
如图：当前节点是40，应该迭代到当前节点是父节点的右节点时，所以要迭代到45。 

5.5   ==与！=操作

对于==与！=操作就是判断数据是否相等。

bool operator!=(const Self& s)
{
	return _node != s._node;
}
bool operator==(const Self& s)
{
	return _node == s._node;
}

六.   Map整体封装

对于Map来说，需要多一个operator[]操作。

由于我们知道，Map里面的Key是不能随意改变的，所以加上const修饰。

namespace yjy {
	template<class K,class T>
	class Map
	{
		struct MapKeyOfT
		{
			const K& operator()(const pair<K,T>& kt)
			{
				return kt.first;
			}
		};
	public:
		typedef typename RBTree<K, pair<const K,T>, MapKeyOfT>::iterator iterator;
		typedef typename RBTree<K, pair<const K,T>, MapKeyOfT>::const_iterator const_iterator;
		iterator begin()
		{
			return _map.begin();
		}
		iterator end()
		{
			return _map.end();
		}
		const_iterator begin() const
		{
			return _map.begin();
		}
		const_iterator end() const
		{
			return _map.end();
		}
		pair<iterator,bool> Insert(const pair<K,T>& kt)
		{
			return _map.Insert(kt);
		}
		iterator Find(const K& k)
		{
			return _map.Find(k);
		}
		T& operator[](const K& key)
		{
			pair<iterator, bool> ret = Insert(make_pair(key, T()));
			return ret.first->second;
		}
	private:
		RBTree<K, pair<const K,T>, MapKeyOfT> _map;
	};
}

七.   Set整体封装

此处的Key也要加上const修饰，因为是不可改变的。

namespace yjy {
	template<class K>
	class Set
	{
		struct SetKeyOfT
		{
			const K& operator()(const K& key)
			{
				return key;
			}
		};
	public:
		typedef typename RBTree<K,const K, SetKeyOfT>::iterator iterator;
		typedef typename RBTree<K, const K, SetKeyOfT>::const_iterator const_iterator;

		iterator begin()
		{
			return _set.begin();
		}
		iterator end()
		{
			return _set.end();
		}
		const_iterator begin() const
		{
			return _set.begin();
		}
		const_iterator end() const
		{
			return _set.end();
		}
		pair<iterator, bool> Insert(const K& key)
		{
			return _set.Insert(key);
		}
		iterator Find(const K& k)
		{
			return _set.Find(k);
		}
	private:
		RBTree<K,const K, SetKeyOfT> _set;
	};
}

八.   红黑树整体封装

#include<iostream>
#include<vector>
using namespace std;
enum Colour
{
	RED,
	BLACK
};
template<class T>
struct RBTreeNode
{
	RBTreeNode<T>* _left;
	RBTreeNode<T>* _right;
	RBTreeNode<T>* _parent;
	Colour _col;
	T _data;
	RBTreeNode(const T& data)
		:_left(nullptr)
		,_right(nullptr)
		,_parent(nullptr)
		,_col(RED)
		,_data(data)
	{}
};
template<class T,class Ptr,class Ref>
struct RBTreeIterator
{
	typedef RBTreeNode<T> Node;
	typedef RBTreeIterator<T,Ptr,Ref> Self;
	Node* _node;
	RBTreeIterator(Node* node)
		:_node(node)
	{}
	Ref operator*()
	{
		return _node->_data;
	}
	Ptr operator->()
	{
		return &_node->_data;
	}
	Self& operator++()
	{
		if (_node->_right)//右边不为空
		{
			//右子树的最左边节点
			Node* subright = _node->_right;
			while (subright->_left)
			{
				subright = subright->_left;
			}
			_node = subright;
		}
		else
		{
			//祖先里面孩子是父亲左的那个
			Node* cur = _node;
			Node* subparent = _node->_parent;
			while (subparent&&subparent->_right == cur)
			{
				cur = subparent;
				subparent = subparent->_parent;
			}
			_node = subparent;
		}
		return *this;
	}
	Self& operator--()
	{
		if (_node->_parent==nullptr)
		{
			Node* maxright = _node;
			while (maxright->_right)
			{
				maxright = maxright->_right;
			}
			_node = maxright;
		}
		else if (_node->_left)//左边不为空
		{
			//左子树的最右边节点
			Node* subright = _node->_left;
			while (subright->_right)
			{
				subright = subright->_right;
			}
			_node = subright;
		}
		else
		{
			//祖先里面孩子是父亲右的那个
			Node* cur = _node;
			Node* subparent = _node->_parent;
			while (subparent && subparent->_left == cur)
			{
				cur = subparent;
				subparent = subparent->_parent;
			}
			_node = subparent;
		}
		return *this;
	}
	bool operator!=(const Self& s)
	{
		return _node != s._node;
	}
	bool operator==(const Self& s)
	{
		return _node == s._node;
	}
};

//Set->RBTree<K,K,SetKeyOfT>
//Map->RBTree<K,pair<K,V>,MapKeyOfT>

//KeyOfT仿函数，取出T对象中的key
template<class K,class T,class KeyOfT>
class RBTree
{
	typedef RBTreeNode<T> Node;
public:
	typedef RBTreeIterator<T,T*,T&> iterator;
	typedef RBTreeIterator<T,const T*,const T&> const_iterator;
	iterator begin()
	{
		Node* subleft = _root;
		while (subleft&&subleft->_left)
		{
			subleft = subleft->_left;
		}
		return iterator(subleft);
	}
	const_iterator begin() const
	{
		Node* subleft = _root;
		while (subleft && subleft->_left)
		{
			subleft = subleft->_left;
		}
		return const_iterator(subleft);
	}
	iterator end()
	{
		return iterator(nullptr);
	}
	const_iterator end() const
	{
		return const_iterator(nullptr);
	}
	iterator Find(const T& data)
	{
		KeyOfT _rot;
		Node* cur = _root;
		while (cur)
		{
			if (_rot(cur->_data) < _rot(data))
			{
				cur = cur->_right;
			}
			else if (_rot(cur->_data) > _rot(data))
			{
				cur = cur->_left;
			}
			else
			{
				return iterator(cur);
			}
		}
		return end();
	}
	pair<iterator,bool> Insert(const T& data)
	{
		if (_root == nullptr)
		{
			_root = new Node(data);
			_root->_col = BLACK;
			return make_pair(iterator(_root), true);
		}
		KeyOfT _rot;
		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (_rot(cur->_data) > _rot(data))
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (_rot(cur->_data) < _rot(data))
			{
				parent = cur;
				cur = cur->_right;
			}
			else
			{
				return make_pair(iterator(cur),true);
			}
		}
		cur = new Node(data);
		Node* newnode = cur;
		if (_rot(parent->_data) < _rot(data))
		{
			parent->_right = cur;
		}
		else
		{
			parent->_left = cur;
		}
		cur->_parent = parent;
		while (parent && parent->_col == RED)
		{
			Node* grandparent = parent->_parent;
			Node* uncle = nullptr;
			//parent和uncle是grandparent的左还是右不影响结果
			//cur是parent的左还是右不影响结果
			if (parent == grandparent->_left)
			{
				uncle = grandparent->_right;
				//uncle存在且为红
				if (uncle && uncle->_col == RED)
				{
					parent->_col = BLACK;
					uncle->_col = BLACK;
					grandparent->_col = RED;
					if (grandparent == _root)
					{
						grandparent->_col = BLACK;
					}
					else
					{
						cur = grandparent;
						parent = cur->_parent;
					}
				}
				else
				{
					//		g
					//	p		u
					//c
					if (cur == parent->_left)
					{
						RotaleR(grandparent);
						parent->_col = BLACK;
						grandparent->_col = RED;
					}
					//		g
					//	p		u
					//		c
					else
					{
						RotaleL(parent);
						RotaleR(grandparent);
						cur->_col = BLACK;
						grandparent->_col = RED;
					}
					break;
				}
			}
			else
			{
				uncle = grandparent->_left;
				if (uncle && uncle->_col == RED)
				{
					parent->_col = BLACK;
					uncle->_col = BLACK;
					grandparent->_col = RED;
					if (grandparent == _root)
					{
						grandparent->_col = BLACK;
					}
					else
					{
						cur = grandparent;
						parent = cur->_parent;
					}
				}
				else
				{
					//		g
					//	u		p
					//				c
					if (cur == parent->_right)
					{
						RotaleL(grandparent);
						parent->_col = BLACK;
						grandparent->_col = RED;
					}
					//		g
					//	u		p
					//		c
					else
					{
						RotaleR(parent);
						RotaleL(grandparent);
						cur->_col = BLACK;
						grandparent->_col = RED;
					}
					break;
				}
			}
		}
		return make_pair(iterator(newnode),true);
	}
	void RotaleL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;
		parent->_right = subRL;
		subR->_left = parent;
		if (subRL)
		{
			subRL->_parent = parent;
		}
		Node* ppnode = parent->_parent;
		parent->_parent = subR;
		if (parent == _root)
		{
			_root = subR;
			subR->_parent = nullptr;
		}
		else
		{
			if (parent == ppnode->_left)
			{
				ppnode->_left = subR;
			}
			else if (parent == ppnode->_right)
			{
				ppnode->_right = subR;
			}
			subR->_parent = ppnode;
		}
	}
	void RotaleR(Node* parent)
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;
		parent->_left = subLR;
		subL->_right = parent;
		if (subLR)
		{
			subLR->_parent = parent;
		}
		Node* ppnode = parent->_parent;
		parent->_parent = subL;
		if (parent == _root)
		{
			_root = subL;
			subL->_parent = nullptr;
		}
		else
		{
			if (ppnode->_left == parent)
			{
				ppnode->_left = subL;
			}
			else if (ppnode->_right == parent)
			{
				ppnode->_right = subL;
			}
			subL->_parent = ppnode;
		}
	}
private:
	Node* _root=nullptr;
};

总结

好了，到这里今天的知识就讲完了，大家有错误一点要在评论指出，我怕我一人搁这瞎bb，没人告诉我错误就寄了。

祝大家越来越好，不用关注我（疯狂暗示）

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1600740.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

CentOS 7开机启动过程，引导和服务，密码的修改

CentOS 7开机启动过程，引导和服务，密码的修改

开机启动过程&#xff1a; 引导过程&#xff1a;1.开机自检(BIOS)->2.MBR引导->GRUB菜单->加载内核kernel->systemd进程初始化 程序&#xff1a;执行特定任务的一串代码&#xff0c;静态&#xff0c;存在硬盘中。 进程&#xff1a;运行中的程序叫进程&#xff0…
阅读更多...
第十一章数据仓库和商务智能10分

第十一章数据仓库和商务智能10分

【数据仓库-后端&#xff0c;商务智能-前端】 基本算法&#xff1a;关联关系&#xff08;牵手-谈恋爱&#xff09;&#xff0c;集群关系&#xff08;杭州人爱吃酸甜口&#xff09;&#xff0c;决策树&#xff0c;线性回归&#xff0c;贝叶斯&#xff0c;神经网络&#xff0c;时…
阅读更多...
【Linux】磁盘扩容到根目录逻辑卷（LVM）

【Linux】磁盘扩容到根目录逻辑卷（LVM）

目录 一、物理卷和逻辑卷 1.物理卷和逻辑卷的区别 2.在Linux系统中查看所有物理卷的信息 3.在Linux系统中查看所有逻辑卷的信息 二、文件系统 三、实操-对root&#xff08;/&#xff09;目录进行扩容 1.使用lsblk命令查看新加入的磁盘信息 2.fdisk -l命令查看系统中磁盘…
阅读更多...
景区导览系统平台|智能导览|数字人导游|VR游园

景区导览系统平台|智能导览|数字人导游|VR游园

随着人工智能、元宇宙等技术的飞速发展&#xff0c;文旅行业正迎来一场前所未有的变革。道可云文旅元宇宙平台以其独特的智慧景区导览系统、元宇宙空间以及数字人导游等创新应用&#xff0c;为景区和游客带来了全新的旅游体验&#xff0c;也标志着文旅行业正式步入了元宇宙时代…
阅读更多...
含多种需求响应及电动汽车的微网/虚拟电厂日前优化调度

含多种需求响应及电动汽车的微网/虚拟电厂日前优化调度

1 主要内容 程序主要建立一个微网/虚拟电厂的日前优化调度模型&#xff0c;以燃气轮机运行成本、购售电费用、电动汽车电池损耗成本以及需求响应费用之和为目标&#xff0c;在日前经济调度模型中&#xff0c;加入了电动汽车模型&#xff0c;考虑了电动汽车出行规律以及充放电规…
阅读更多...
华硕ROG幻16笔记本电脑模式切换管理工具完美替代华硕奥创中心管理工具

华硕ROG幻16笔记本电脑模式切换管理工具完美替代华硕奥创中心管理工具

文章目录 华硕ROG幻16笔记本电脑模式切换管理工具完美替代华硕奥创中心管理工具1. 介绍2. 下载3. 静音模式、平衡模式、增强模式配置4. 配置电源方案与模式切换绑定5. 启动Ghelper控制面板6. 目前支持的设备型号 华硕ROG幻16笔记本电脑模式切换管理工具完美替代华硕奥创中心管理…
阅读更多...
环境搭建创建项目_使用DevEco开发工具进行开发_创建项目_认识项目结构---HarmonyOS4.0+鸿蒙NEXT工作笔记001

环境搭建创建项目_使用DevEco开发工具进行开发_创建项目_认识项目结构---HarmonyOS4.0+鸿蒙NEXT工作笔记001

首先去下载DevEco Studio然后再去安装就可以了 安装下一步下一步非常简单 首先去安装nodejs,可以看到,有两个安装方法,左边是自己安装的制定文件夹就可以了,然后 右边是使用鸿蒙自带的,我们选择第二个 然后我们看这个ohpm其实就跟npm是一个意思,用来管理鸿蒙的包的. 这里我们…
阅读更多...
JavaEE：JVM

JavaEE：JVM

基本介绍 JVM&#xff1a;Java虚拟机&#xff0c;用于解释执行Java字节码 jdk&#xff1a;Java开发工具包 jre&#xff1a;Java运行时环境 C语言将写入的程序直接编译成二进制的机器语言&#xff0c;而java不想重新编译&#xff0c;希望能直接执行。Java先通过javac把.java…
阅读更多...
【机器学习】贝叶斯算法在机器学习中的应用与实例分析

【机器学习】贝叶斯算法在机器学习中的应用与实例分析

贝叶斯算法在机器学习中的应用与实例分析 一、贝叶斯算法原理及重要性二、朴素贝叶斯分类器的实现三、贝叶斯网络在自然语言处理中的应用四、总结与展望 在人工智能的浪潮中&#xff0c;机器学习以其独特的魅力引领着科技领域的创新。其中&#xff0c;贝叶斯算法以其概率推理的…
阅读更多...
用于密集视觉冲击的紧凑三维高斯散射Compact 3D Gaussian Splatting For Dense Visual SLAM

用于密集视觉冲击的紧凑三维高斯散射Compact 3D Gaussian Splatting For Dense Visual SLAM

Compact 3D Gaussian Splatting For Dense Visual SLAM 用于密集视觉冲击的紧凑三维高斯散射 Tianchen Deng 邓天辰11Yaohui Chen 陈耀辉11Leyan Zhang 张乐妍11Jianfei Yang 杨健飞22Shenghai Yuan 圣海元22Danwei Wang 王丹伟22Weidong Chen 陈卫东11 Abstract 摘要 …
阅读更多...
通过腾讯云搭建跨境电商demo的详细操作过程(建站系统 保姆级指导，巨详细)

通过腾讯云搭建跨境电商demo的详细操作过程(建站系统 保姆级指导，巨详细)

引言&#xff1a; 有许多做跨境电商的朋友&#xff0c;或者为跨境电商服务的小企业&#xff0c;都会面临搭建电商平台V1.0的问题 因此&#xff0c;花了点时间&#xff0c;找了一个开源的项目&#xff0c;让大家可以跑起来&#xff0c;一方面了解平台都有哪些模块&#xff0c;另…
阅读更多...
Unity 左右折叠显示与隐藏UI的简单实现

Unity 左右折叠显示与隐藏UI的简单实现

要实现一个简单的UI左右折叠显示与隐藏&#xff0c;可以结合遮罩&#xff0c;通过代码控制UI区块的宽度和位移来实现。 具体可以按以下步骤实现&#xff1a; 1、新建一个Image组件&#xff0c;并添加精灵&#xff0c;调整大小后&#xff0c;复制一份作为该UI的父物体&#xf…
阅读更多...
1、MYSQL系列-深入理解Mysql索引底层数据结构与算法

1、MYSQL系列-深入理解Mysql索引底层数据结构与算法

索引的本质 索引是帮助MySQL高效获取数据的排好序的数据结构 索引数据结构 二叉树红黑树Hash表BTree B-Tree B-Tree 叶节点具有相同的深度&#xff0c;叶节点的指针为空&#xff0c;所有索引元素不重复&#xff0c;节点中的数据索引从左到右递增排列 BTree(B-Tree变种) 非叶…
阅读更多...
Pytorch搭建GoogleNet神经网络

Pytorch搭建GoogleNet神经网络

一、创建卷积模板文件 因为每次使用卷积层都需要调用Con2d和relu激活函数&#xff0c;每次都调用非常麻烦&#xff0c;就将他们打包在一起写成一个类。 in_channels&#xff1a;输入矩阵深度作为参数输入 out_channels: 输出矩阵深度作为参数输入 经过卷积层和relu激活函数…
阅读更多...
Qt对象池，单例模式，对象池可以存储其他类的对象指针

Qt对象池，单例模式，对象池可以存储其他类的对象指针

代码描述&#xff1a; 写了一个类&#xff0c;命名为对象池&#xff08;ObjectPool &#xff09;&#xff0c;里面放个map容器。 3个功能&#xff1a;添加对象&#xff0c;删除对象&#xff0c;查找对象 该类只构建一次&#xff0c;故采用单例模式功能描述&#xff1a;对象池可…
阅读更多...
04 MySQL --DQL 专题--Union、exists

04 MySQL --DQL 专题--Union、exists

1. UNION、UNION ALL UNION 关键字的作用&#xff1f; 合并两个或多个 SELECT 语句的结果。发挥的作用与 or 非常相似 UNION关键字生效的前提&#xff1f; 每个 SELECT 语句必须拥有相同数量的列。每个 SELECT 语句中的列的顺序必须相同。列必须拥有相似的数据类型。 SELEC…
阅读更多...
WebRTC直播间搭建记录

WebRTC直播间搭建记录

考虑到后续增加平台直播的可能性&#xff0c;笔记记录一下WebRTC相关. 让我们分别分析两种情况下的WebRTC连接建立过程&#xff1a; 情况一&#xff1a;AB之间可以直接通信 1.信令交换&#xff1a; 设备A和设备B首先通过信令服务器交换SDP&#xff08;Session Description Pr…
阅读更多...
负载均衡集群——LVS

负载均衡集群——LVS

目录 1.LVS简介 2.LVS体系结构 3.LVS相关术语 4. LVS工作模式 5. LVS调度算法 6.LVS集群介绍 6.1 LVS-DR模式 6.2 LVS – NAT 模式 6.3 LVS – TUN 模式 7.LVS 集群构建 7.1 LVS/NAT 模式配置 实验操作步骤 步骤 1 Nginx1 和 Nginx2 配置 步骤 2 安装和配置 LVS …
阅读更多...
R语言使用installr包对R包进行整体迁移

R语言使用installr包对R包进行整体迁移

今天分享一个R语言的实用小技巧&#xff0c;如果咱们重新安装了电脑&#xff08;我重装了电脑&#xff09;或者因为需要卸载旧版本的R软件&#xff0c;安装新版本的R&#xff0c;那么必然会造成R包的库缺失&#xff0c;需要重新下载&#xff0c;有些还不是官方的R包&#xff0c…
阅读更多...
如何从零开始创建React应用：简易指南

如何从零开始创建React应用：简易指南

&#x1f31f; 前言 欢迎来到我的技术小宇宙&#xff01;&#x1f30c; 这里不仅是我记录技术点滴的后花园&#xff0c;也是我分享学习心得和项目经验的乐园。&#x1f4da; 无论你是技术小白还是资深大牛&#xff0c;这里总有一些内容能触动你的好奇心。&#x1f50d; &#x…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023