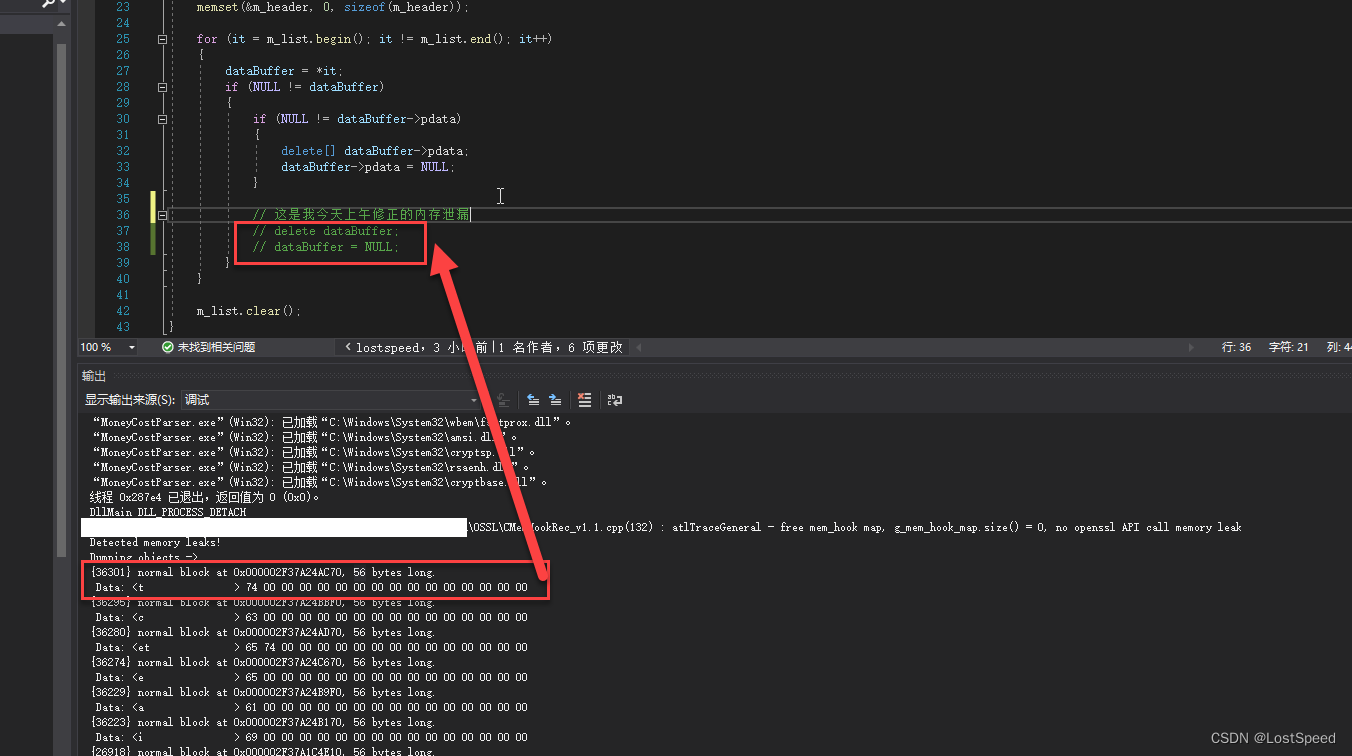
• 任何一个函数都可以看成是若干个三角函数的加权和

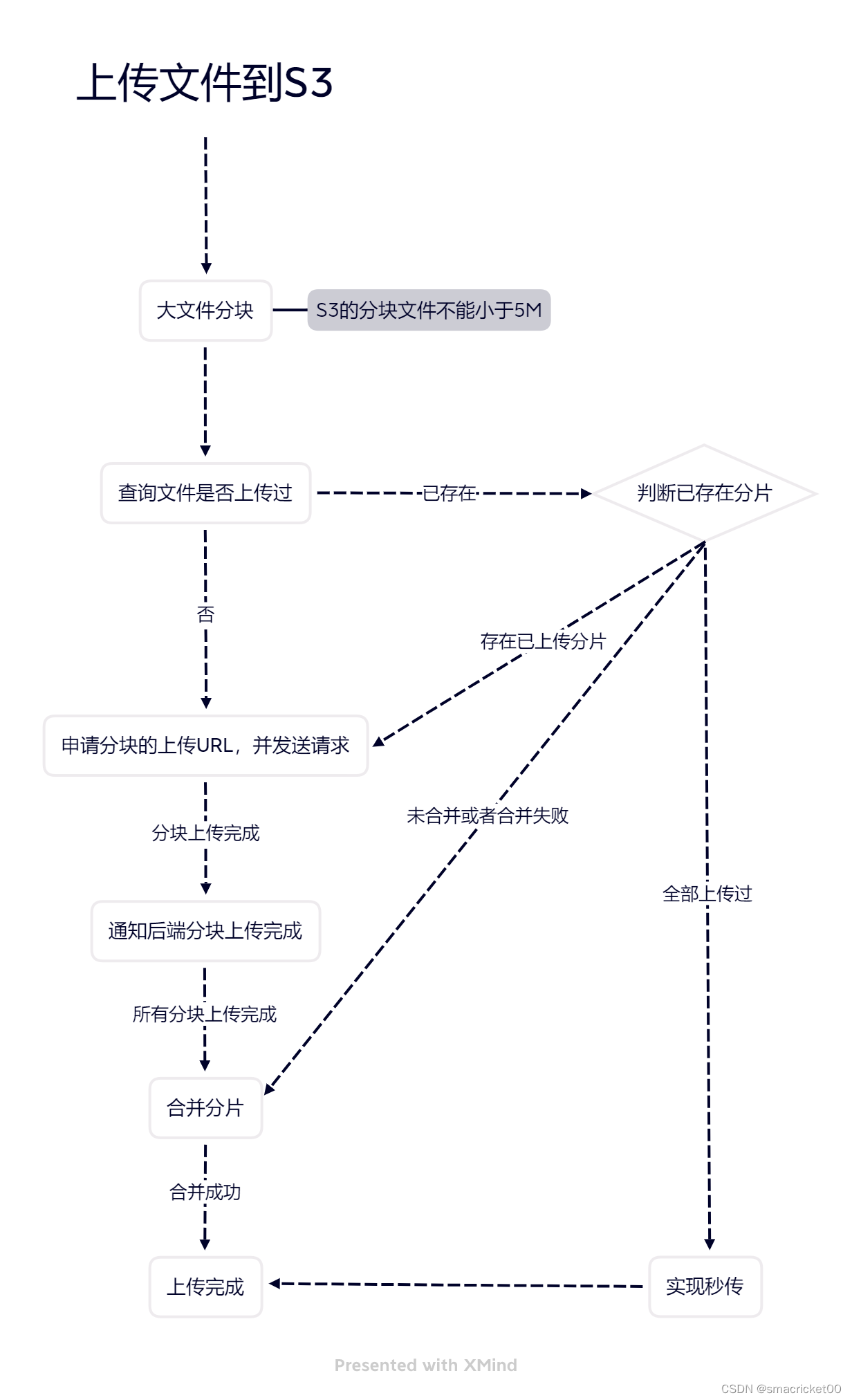
一、傅里叶变换

1、推导过程

资料：https://www.bilibili.com/video/BV1pW411J7s8/?spm_id_from=333.1007.top_right_bar_window_history.content.click

（1）$e^{i\theta }$代表复数域内的旋转

• 上面的公式是欧拉公式，右侧表示的几何意义就是在复数平面内（横轴是实数、纵轴是虚数）旋转$\theta$。

（2）将一个正弦波缠绕在圆上

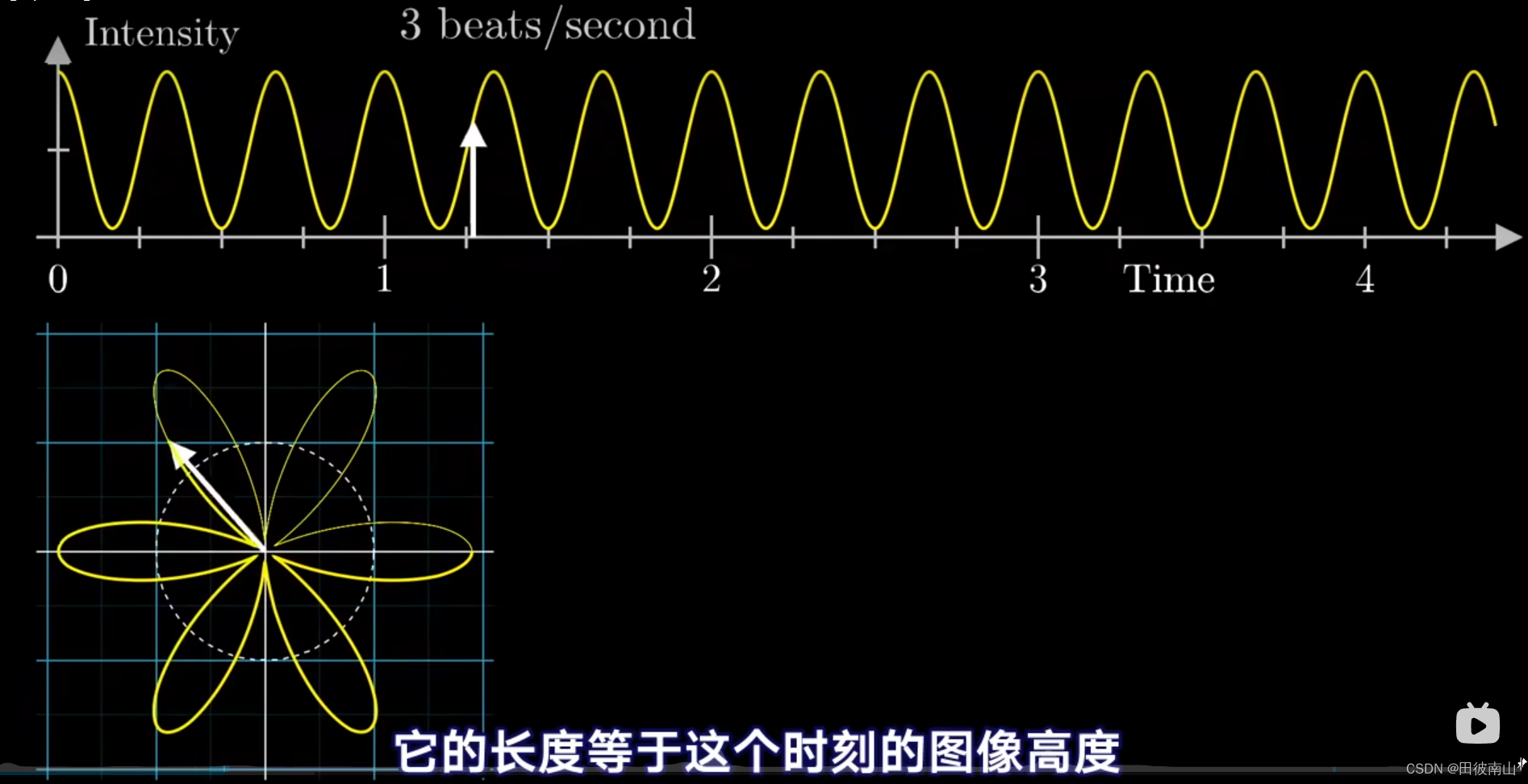
• 上图中将一个有固定频率的三角函数缠绕成了一个圆上，白色的箭头代表一个向量，向量的长度代表上面三角函数的幅度，向量的角度代表上面的向量移动的位置。当向量以特定的速度平移时，一圈上“突出”的个数也是相同的，这个速度可以转换到这个圆上的一个频率，比如图中的3拍每秒。
  

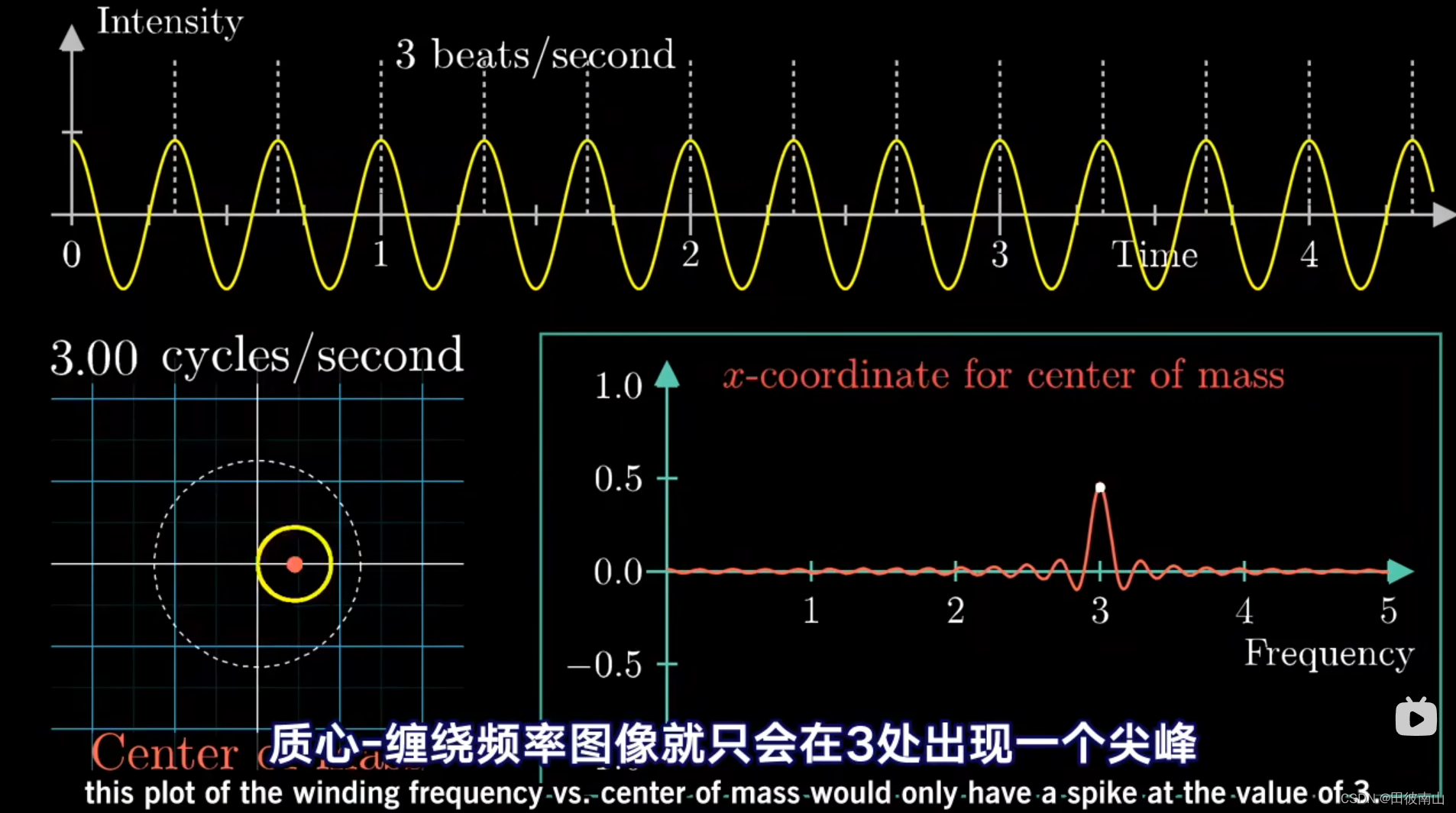
• 当上面说的这个频率是与三角函数本身的频率相同时，整个图形的质心会很特别的偏离中心。以这个偏离程度为纵轴，向量的频率为横轴，就可以画出右下角那个图。通过这个方法，如果我们可以调节这个向量的频率并采集质心的位置就可以获得这个三角函数的频率。

（3）多个正弦波的叠加组成

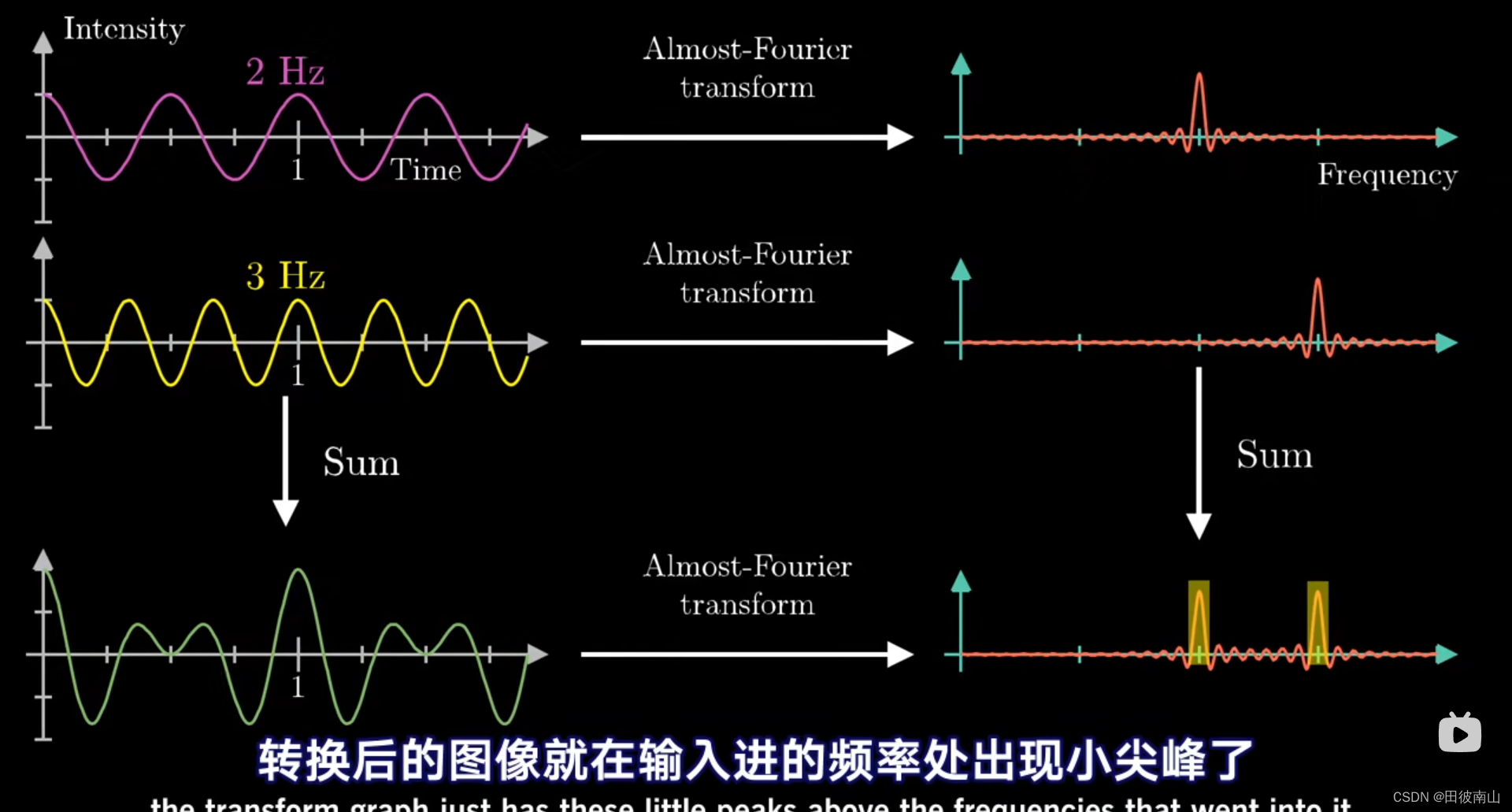
• 上图中是将两个余弦波叠加后，通过之前提到的那个方法，找到了两个余弦的频率。
• 参考最开始的那个结论，就可以找到组成任意函数的若干三角函数

（4）如何获得质心的位置

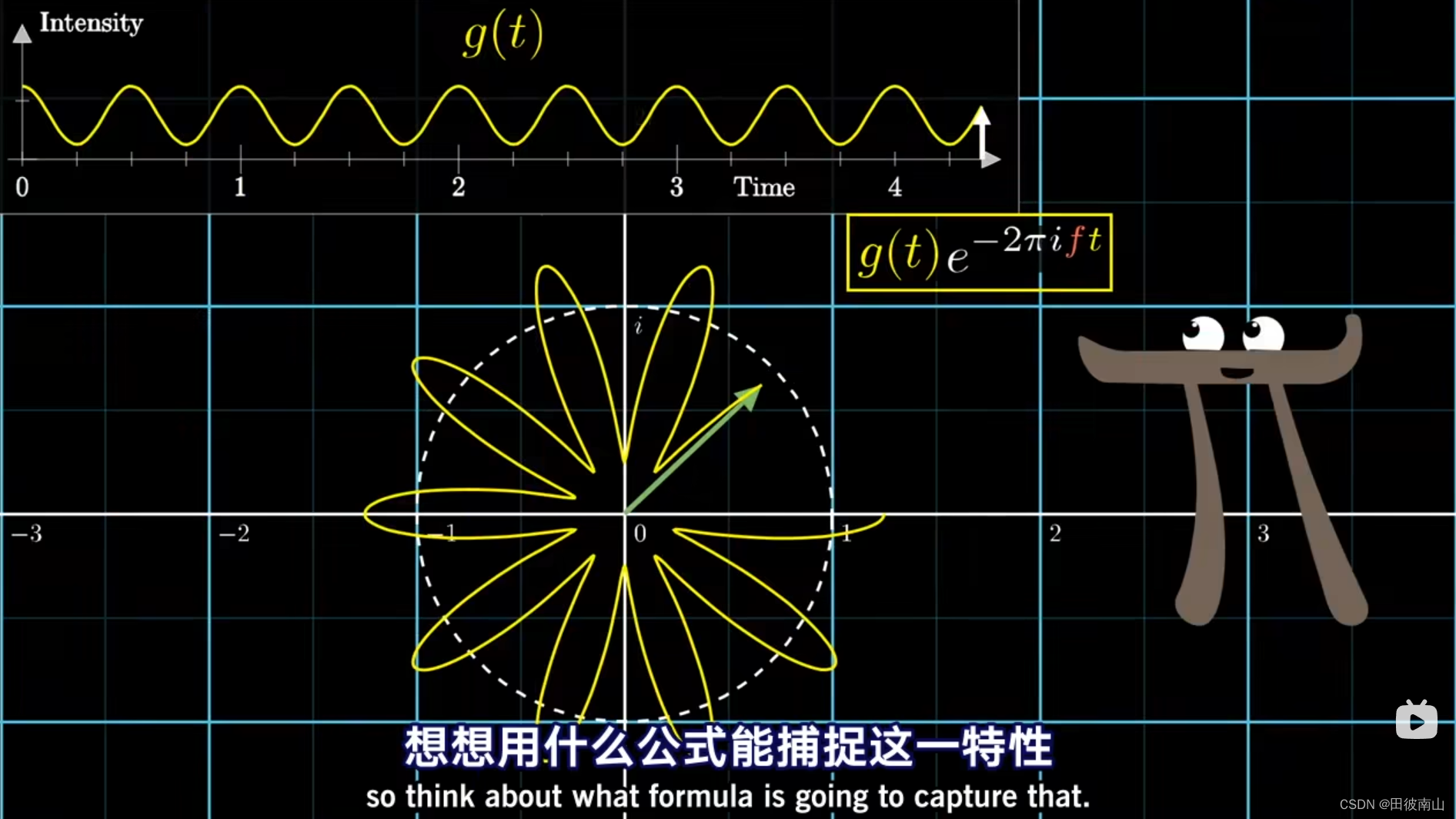
• 上图中g(t)是三角函数，黄色框框柱的是缠绕在圆上的这个图像。
  

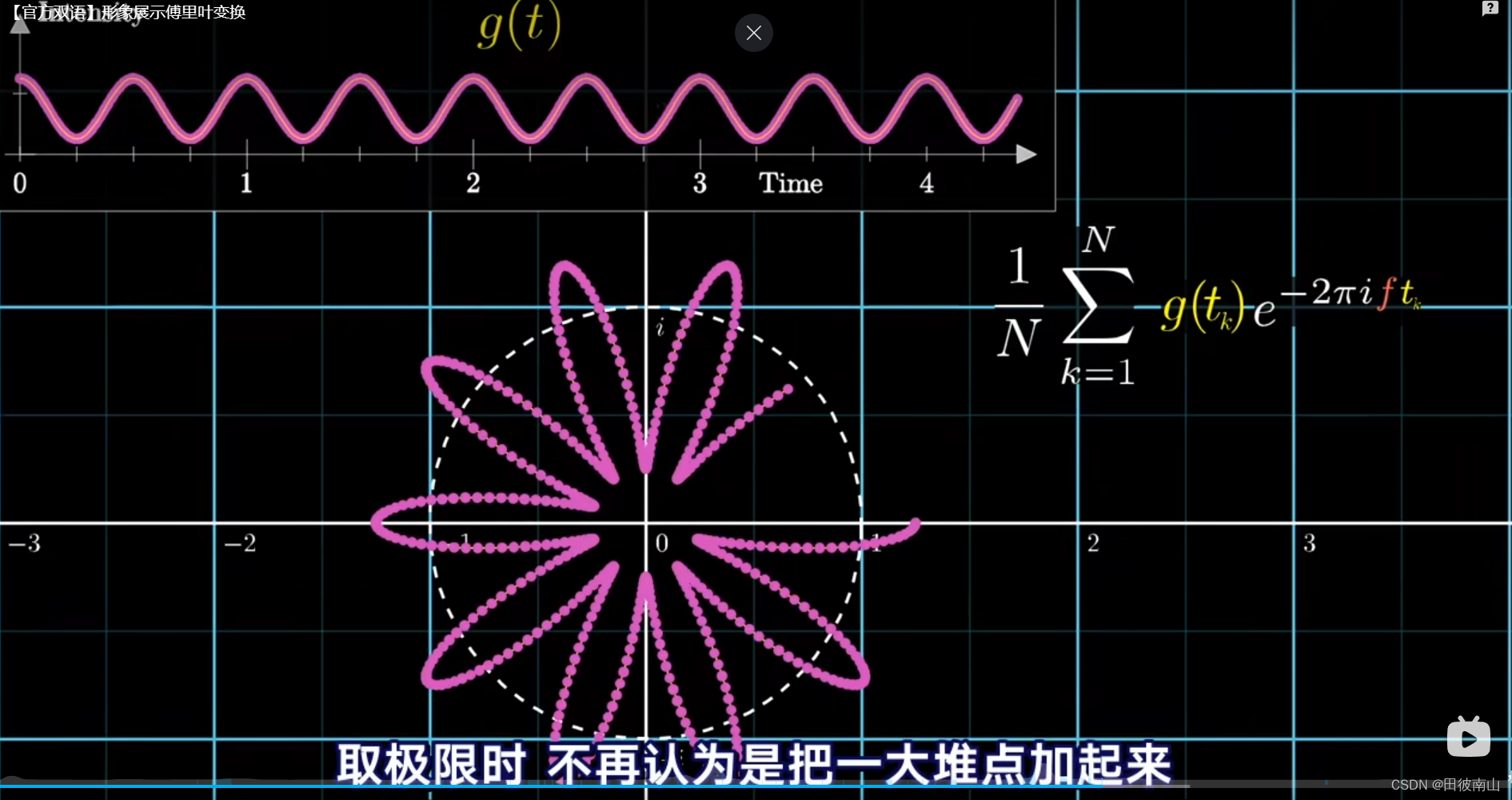
• 在这缠绕在圆上的图像上采集若干个点并且平均，那么这个结果就应该是质心的位置。
  

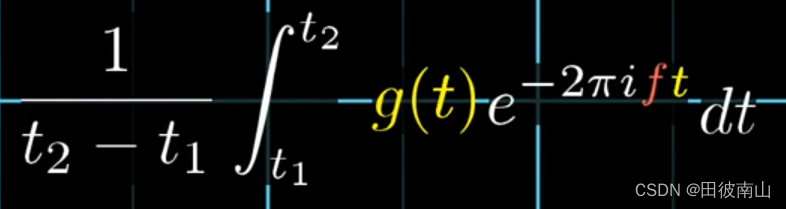
• 将若干个点推广到无穷多个点后，就用积分代替累加符号，得到上面这个公式

（5）最终获得傅里叶变换

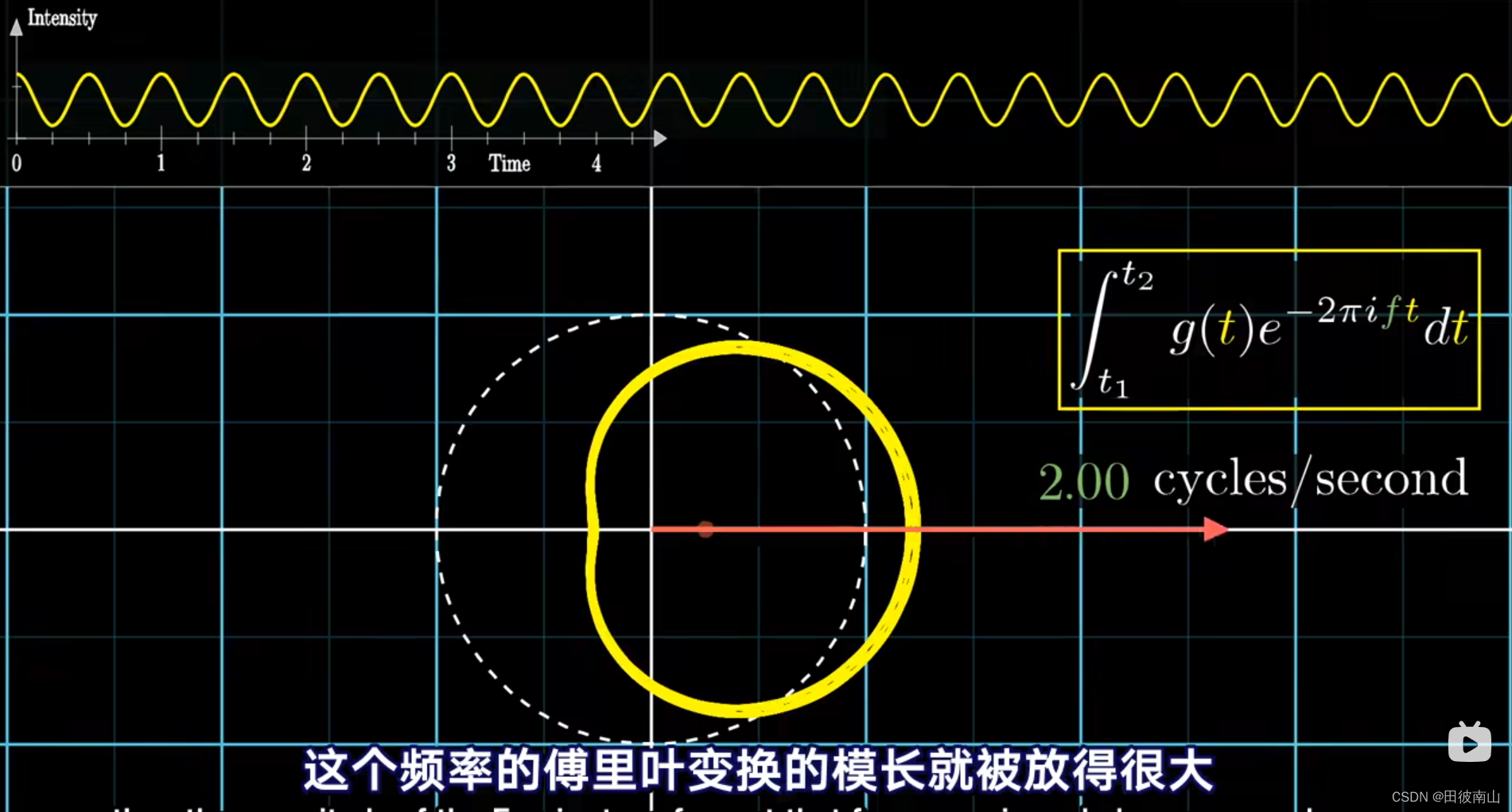
• 考虑到我们实际的用处，如果一个频率的信号反复持续，那么其模长应该不断累计，所以不再需要除以时间。
  
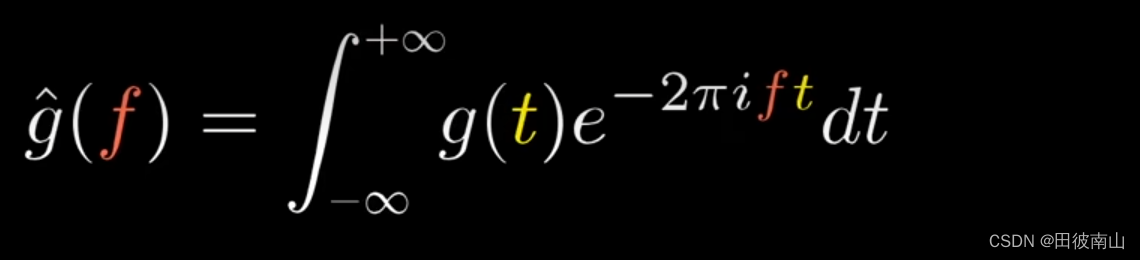
• 将上面的公式中积分的时间上下界拓宽到正负无穷
  
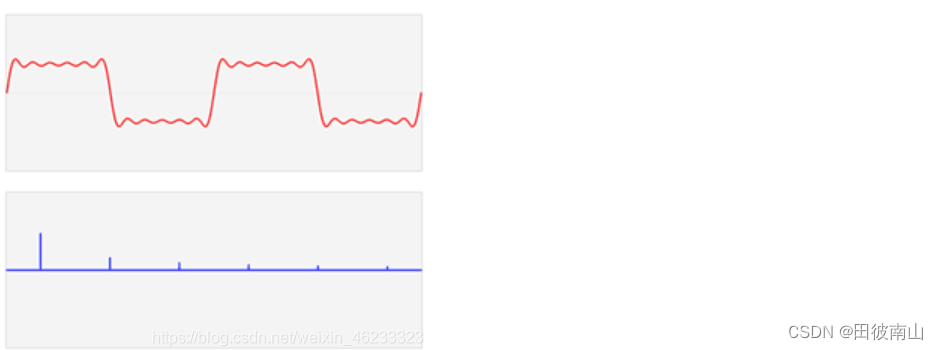
• 通过上面的操作，红色的信号可以被分解为下面的频谱图，横轴是频率，纵轴是幅度

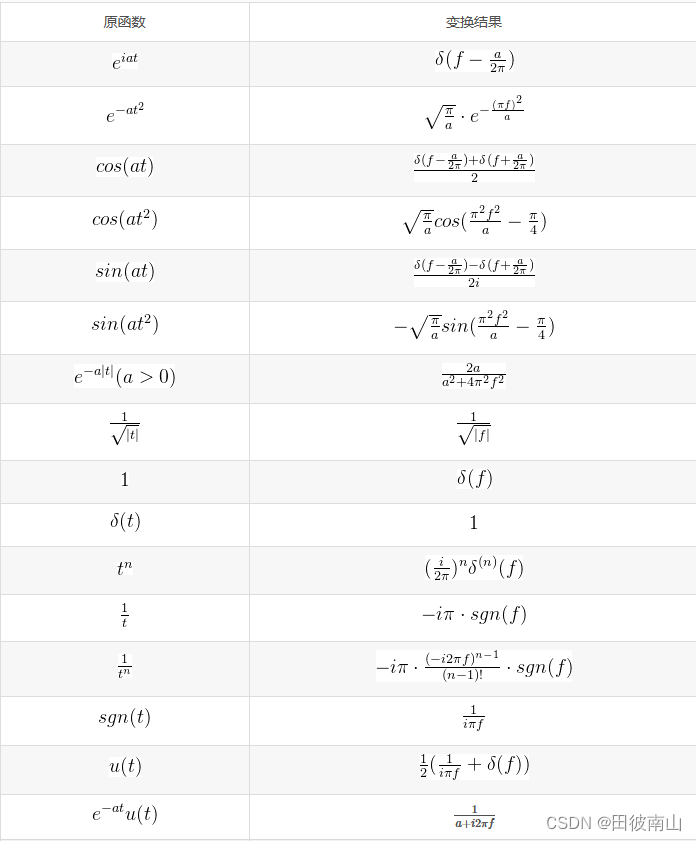
2、常见傅里叶变换

性质：https://blog.csdn.net/Chandler_river/article/details/133827638
计算过程：https://blog.csdn.net/qq_42667481/article/details/107976565

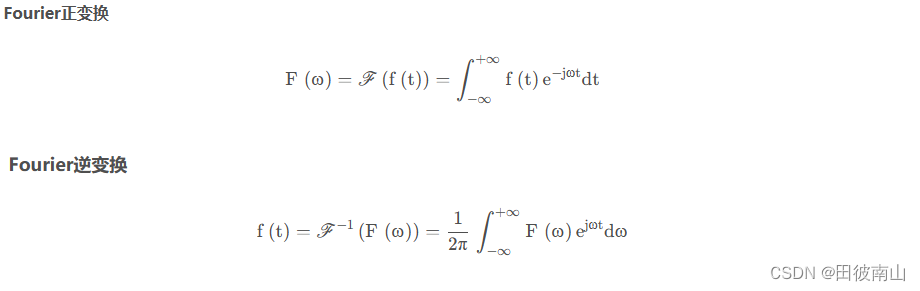
二、拉普拉斯变换

• 个人理解拉普拉斯变换只是傅里叶变换的延伸，将其从频域转换到实用性更广并且便于计算的复数域
  资料：https://blog.csdn.net/wh_STUDY/article/details/126403817

三、Z变换

1、离散傅里叶变换

资料：https://www.bilibili.com/video/BV1kg4y1U7gc/?spm_id_from=333.788.top_right_bar_window_default_collection.content.click&vd_source=a686d8f8b0e9b94066f2d4ba714466e7

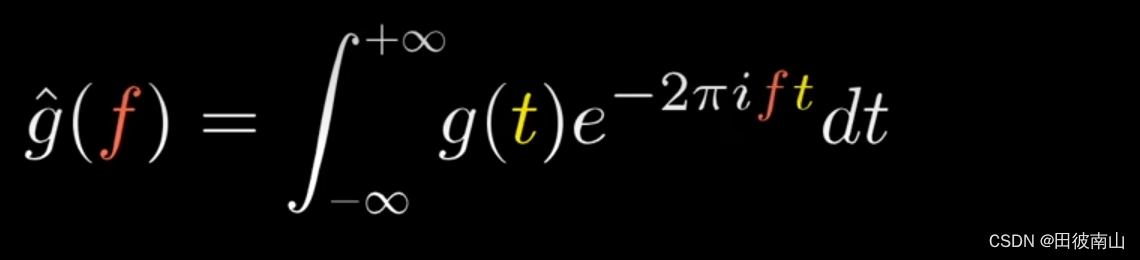
• K对应频率f，n对应时间t，

2、Z变换

资料：https://www.bilibili.com/video/BV1XW411s7s9/?spm_id_from=333.788.top_right_bar_window_default_collection.content.click