代码随想录算法训练营第四十一天|343.整数拆分、96.不同的二叉搜索树
343.整数拆分
给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k >= 2 ),并使这些整数的乘积最大化。
返回 你可以获得的最大乘积 。
示例 1:
输入: n = 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1。
题解:将数字尽可能拆分成m个近似相等的子数,这样乘积才最大。
- dp[i]:数 I 拆分后对应的子数的乘积
- 递推公式:dp[i]=max(dp[j]*dp[i-j],dp[i])
- dp数组初始化 : dp[0]=1,dp[1]=0,dp[2]=1;
- 遍历顺序:从前向后
- 打印dp数组
代码:
class Solution {
public int integerBreak(int n) {
//数 n 对应的数组大小是n+1;
int [] dp=new int[n+1];
dp[1]=0;
dp[2]=1;
for(int i=3;i<=n;i++){
for(int j=1;j<=i-j;j++){
//数的划分可以分成两种情况,分成 j 和 i-j ;j 和 dp[i-j]
//将数分成两个整数,或者将整数拆分成两个及两个以上的整数
dp[i]=Math.max(dp[i],Math.max(j*(i-j),j*dp[i-j]));
}
}
return dp[n];
}
}
96.不同的二叉搜索树
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
示例 1:
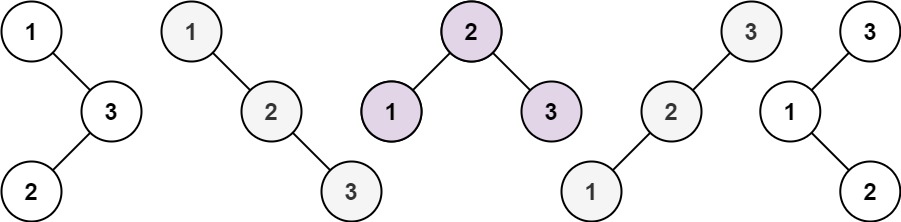
输入:n = 3
输出:5
题解:
-
dp[i]:输入 i 有 dp[i]种不同的二叉树
-
递推公式:二叉树的个数=左子树的个数*右子树的个数。
dp[i]+=dp[j-1]*dp[i-j];dp[j-1] :左节点个数 dp[i-j]:右节点个数 -
初始化:dp[0]=0 dp[1]=1
-
遍历顺序:从前往后
-
打印dp数组
代码:
class Solution {
public int numTrees(int n) {
int [] dp=new int[n+1];
//空节点也是一颗二叉树
dp[0]=1;
dp[1]=1;
for(int i=2;i<=n;i++){
//遍历直到 i 为头结点的情况
for(int j=1;j<=i;j++){
dp[i]+=dp[j-1]*dp[i-j];
}
}
return dp[n];
}
}