4/14/2024
128.最长连续序列
自己的
这是前两天做一半的题目了。这题给我的教训就是用哈希表的时候一定一定要考虑重复元素的问题!!!!
这题让我想到了最长递增子序列,只是名字有点像。子序列和子数组还不一样一个连续一个不连续。自己一开始的做法是把每个元素作为key,是否被访问过作为value来存入hash表里,然后对数组元素进行遍历,访问了首先value为true,然后双指针分别标记前一个数 nums-1 和后一个数nums+1 ,分别向前和向后迭代更新,指针相减即为长度,迭代最大长度即可。
注意boolean的布尔类型为Boolean
一个for循环引发的错误,但是你这个方法也好慢啊。。

class Solution {
public int longestConsecutive(int[] nums) {
HashMap<Integer, Boolean> hash = new HashMap<>();
int res = 0;
for(int x : nums){
hash.put(x, false);
}
for(int i = 0; i < nums.length; i++){
// 原来的这个if条件写在了for循环的条件里
// 这样不就只找了一次,
if(hash.get(nums[i]) == false){
//我说怎么慢,访问这个元素也要改为true,之前忘了
hash.replace(nums[i], true);
int low = 0;
int fast = 0;
int cur = nums[i];
while(hash.containsKey(cur - 1)){
low--;
hash.replace(cur - 1, true);
cur = cur - 1;
}
// 重置cur;
// 相同元素?
cur = nums[i];
while(hash.containsKey(cur + 1)){
fast++;
hash.replace(cur + 1, true);
cur = cur + 1;
}
int p = fast - low + 1;
res = res > p ? res : p;
}
else continue;
}
return res;
}
}官方
128. 最长连续序列 - 力扣(LeetCode)
官方的题解写的挺好的,用的是hashSet。特别是时间复杂度后面为什么是 O(n) 的时候。

因为每个都会被枚举
class Solution {
public int longestConsecutive(int[] nums) {
Set<Integer> num_set = new HashSet<Integer>();
for (int num : nums) {
num_set.add(num);
}
int longestStreak = 0;
for (int num : num_set) {
if (!num_set.contains(num - 1)) {
int currentNum = num;
int currentStreak = 1;
while (num_set.contains(currentNum + 1)) {
currentNum += 1;
currentStreak += 1;
}
longestStreak = Math.max(longestStreak, currentStreak);
}
}
return longestStreak;
}
}
72.编辑距离
求从word1转换到word2所需的最小操作次数。而操作包括:
插入,删除,替换一个字符。也就是三种。
看了题解,首先长度要一致,如果长度:
- word1 > word2,那么word1要删除字符去对标word2,也等价于word2增加字符,因为求的是次数,这两种次数是一样的。
- word1 < word2,那么word1要增加字符去对标word2,也等价于word2删减字符。
- word1 = word2, 长度匹配了。
那么我们如何定义dp数组的含义?很巧妙的是dp[ i ][ j ]表示从word1的下标(从0开始)为 i 的单词转换为 word2 下标为 j 的单词的最小操作数。
分类讨论,dp[ i ][ j ]从何而来?多维dp也就是二维dp吧,从周围的三个元素:
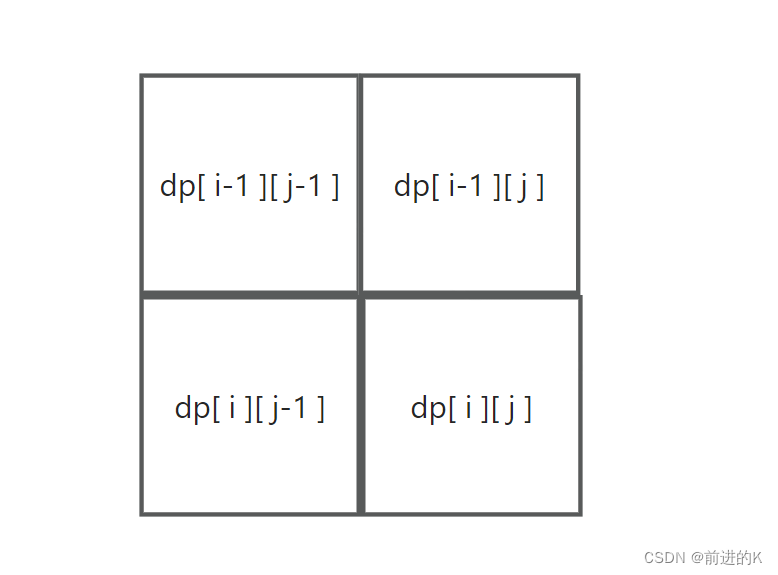
- 如果已知dp[ i -1 ][ j ],也就是知道了从单词1的 i -1 个字符转换到(替换为)单词2 的 j 个字符所需的次数(或者说从单词2的 j 转换为/替换成单词1的 i-1 的最小次数),这里该怎么想呢,还是看了一下题解,
- 如果想得到dp[i][j],也就是对于单词1的第 i 个字符,只要在单词2的前j个单词后面添加一个相同在字符,就可以得到单词1的前i个字符了。
- 这里不要觉得添加一个字符就是j+1了,添加只是一个操作,j代表的是当前遍历到的下标,要求的是次数。而且无论dp[i][j]是从单词1还是单词2变过来的都无所谓,因为是这个变化是等价的,次数是一定的。
- 可以这样理解,我就看单词2的前 j 个字符,固定住,我知道了从单词2的前 j 个字符转换到单词1的前 i -1 个字符的编辑距离/最小操作次数为dp[i-1][j],
- 那么从单词2的前 j 个字符转换到单词1的前 i 个字符,只需要在dp[i-1][j]的这个变化的基础上,(单词2的前 j 个字符已经转换到单词1的前 i -1 个字符)在加一次操作,在单词2的前 j 个字符后加上单词1的第i个字符。
72. 编辑距离 - 力扣(LeetCode)
class Solution {
public int minDistance(String word1, String word2) {
int n = word1.length();
int m = word2.length();
// 有一个字符串为空串
if (n * m == 0) {
return n + m;
}
// DP 数组
int[][] D = new int[n + 1][m + 1];
// 边界状态初始化
for (int i = 0; i < n + 1; i++) {
D[i][0] = i;
}
for (int j = 0; j < m + 1; j++) {
D[0][j] = j;
}
// 计算所有 DP 值
for (int i = 1; i < n + 1; i++) {
for (int j = 1; j < m + 1; j++) {
int left = D[i - 1][j] + 1;
int down = D[i][j - 1] + 1;
int left_down = D[i - 1][j - 1];
if (word1.charAt(i - 1) != word2.charAt(j - 1)) {
left_down += 1;
}
D[i][j] = Math.min(left, Math.min(down, left_down));
}
}
return D[n][m];
}
}