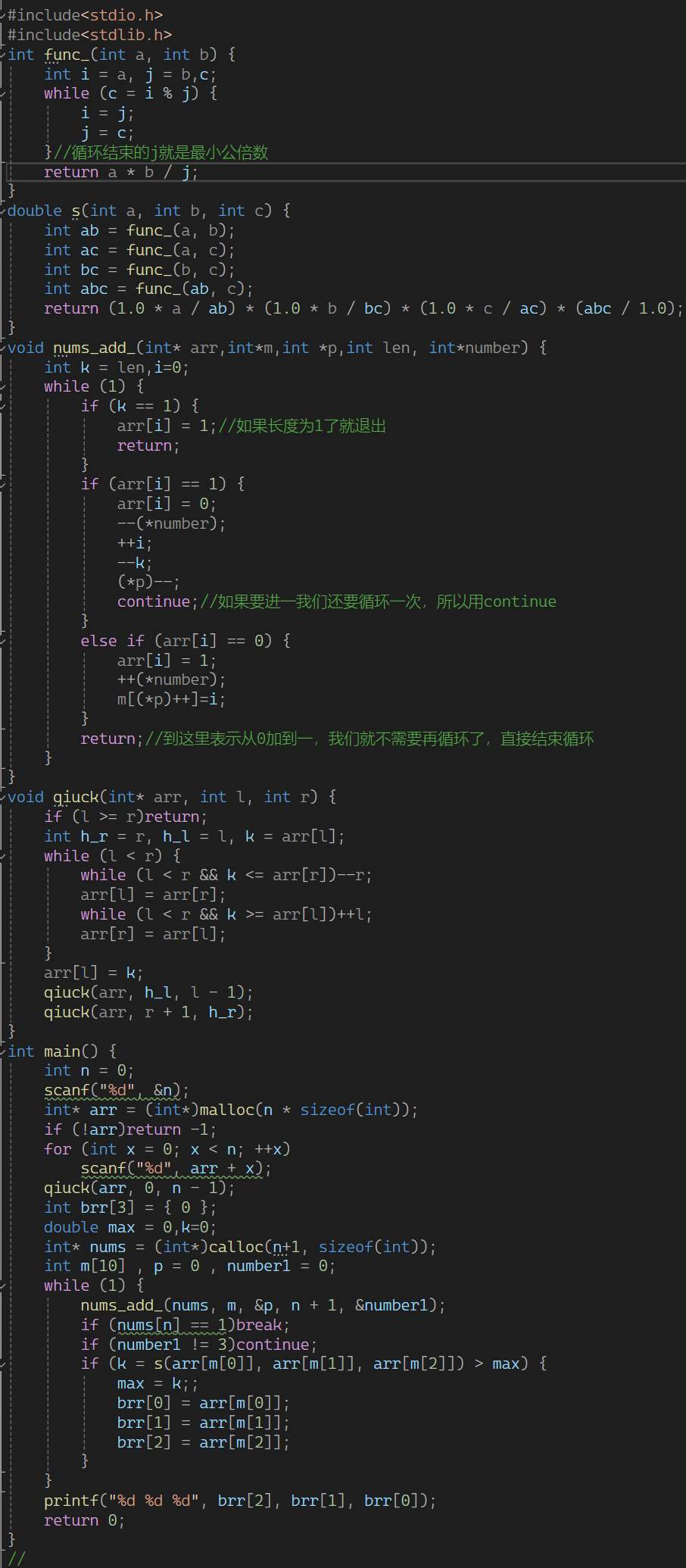
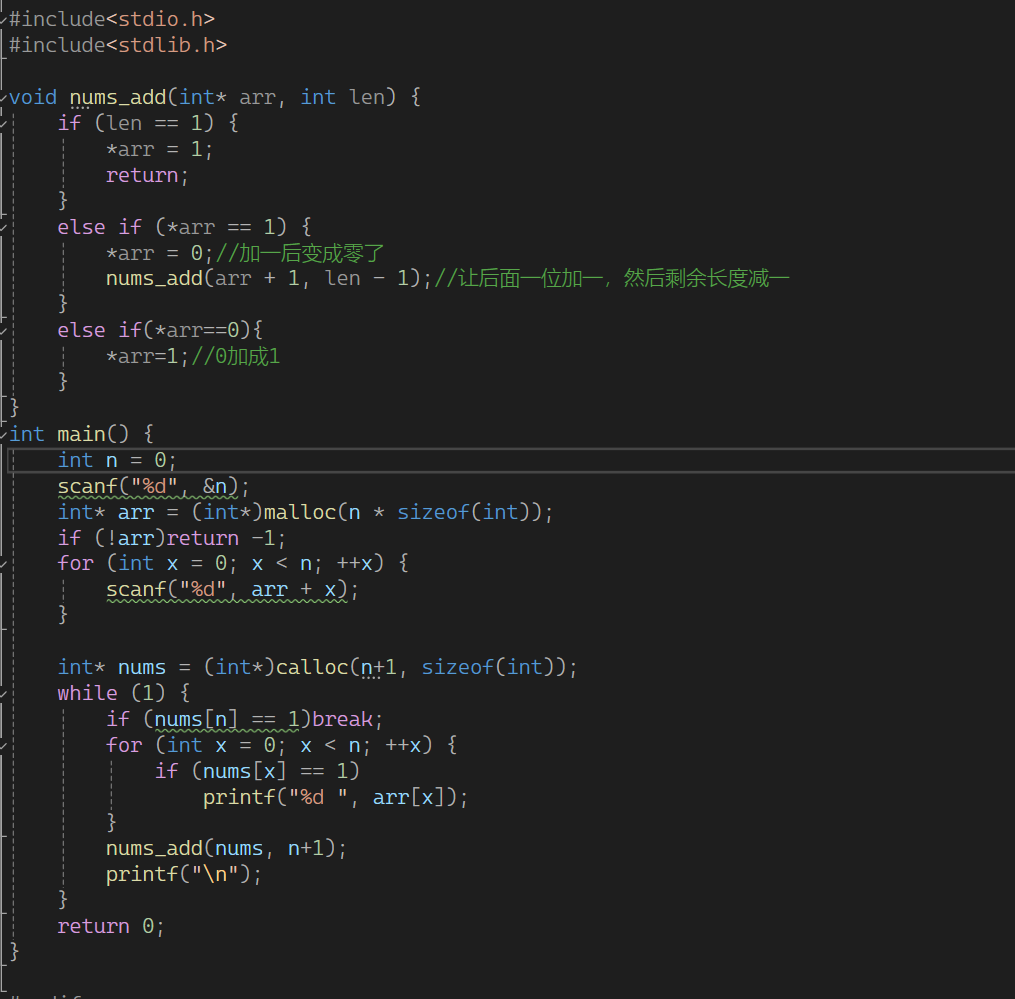
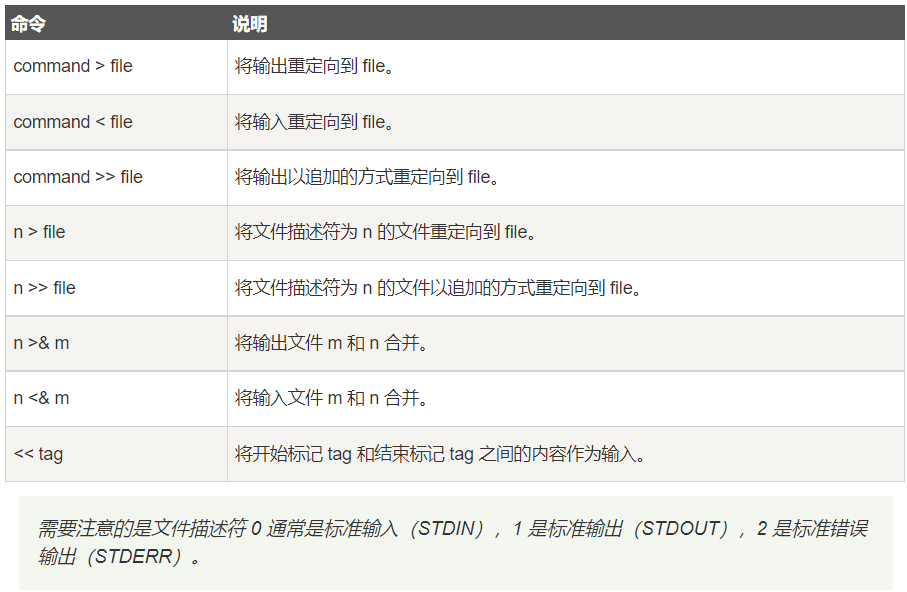
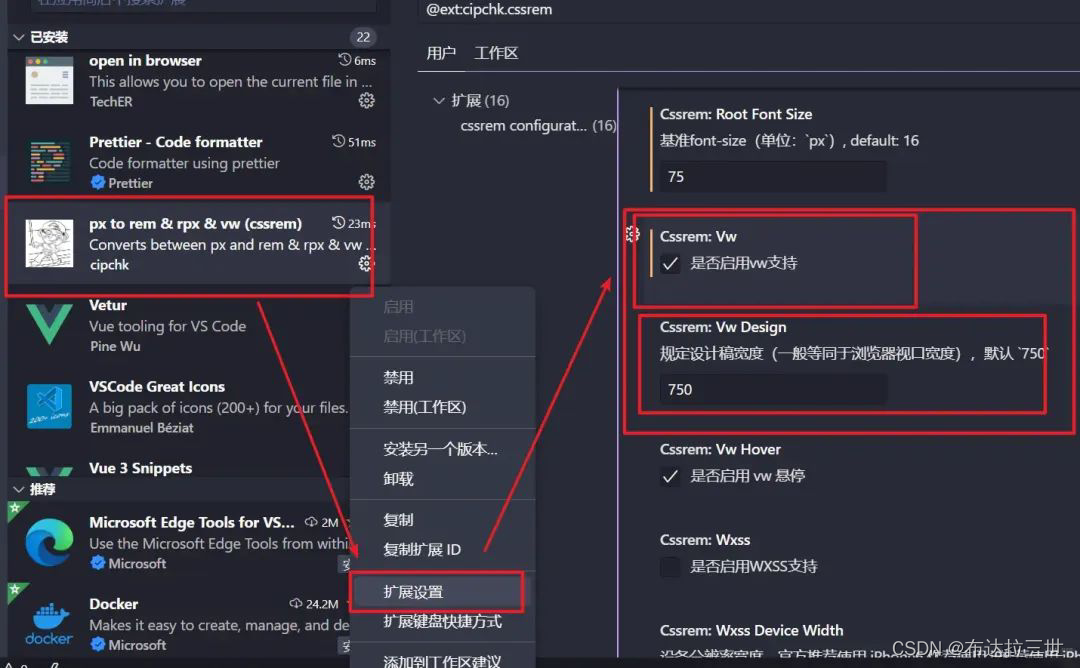
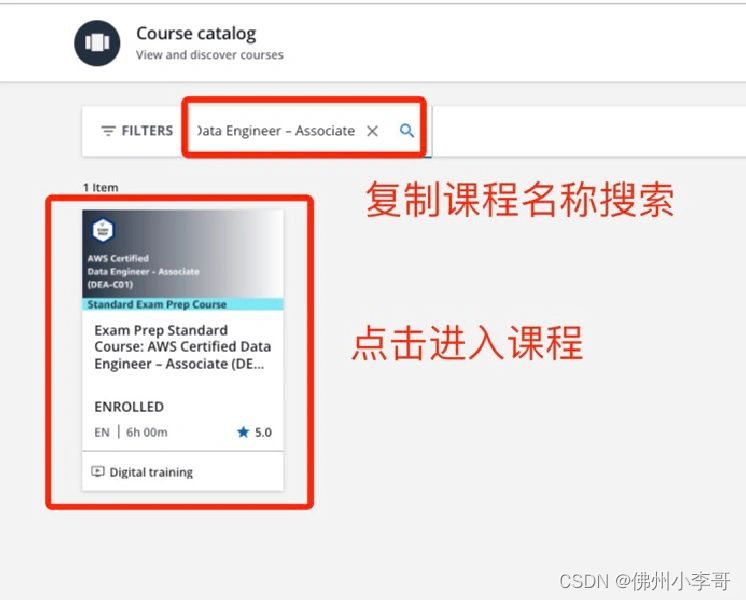
先展示题目


声明
以下代码仅是我的个人看法,在自己考试过程中的优化版,本人考试就踩了很多坑,我会—一列举出来。代码可能很多,但是总体时间复杂度不高只有0(N²)
函数里面的动态数组我没有写开辟判断和free,这里我忽略掉了。
正文
先直接抛出最后的代码:

我也觉得太长了,大家可以当做知识点的掌握来看吧。
从数据中取出n个数的问题-->可以拓展到取出所有子集问题
先讲子集问题
这个问题我们可以用三个for循环来做,但是时间复杂度太高了。所以我们有以下的方法。
一个数取不取就有两种情况。我们可以用0或1来表示。那么我们就可以用二进制来表示我们的取或不取,用每位二进制的位置来对于每个元素。
例如:有1 2 两个数字。我们就可以用两位二进制来表示:00 01 10 11分别表示 不取任何数 取2 取1 都取。一共有2^2次方中情况
那么我们推广到n,就有2^n种。
我们来尝试写一下代码。
直接用二进制
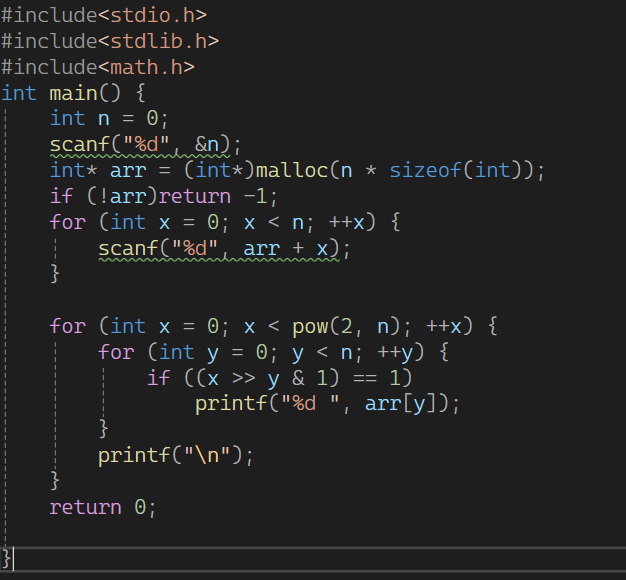

完全没问题。
用数组模拟二进制
这里有一个问题不知道大家看到没:2^n 容易溢出。因此我们可以用数组来模拟二进制的自增。
自增问题涉及到进一问题,所以我们需要运用到递归,递归的判断终止条件就是n+1位由0变成1。
所以我们需要开辟n+1长度的数组nums。
用类似递归来实现
用循环(最优解)

这里几个continue和return一定要有,不然逻辑就错了
这样的话我们就可以遍历任何长度的数组的子集了!
下面把代码给大家
#include<stdio.h>
#include<stdlib.h>
void nums_add(int* arr, int len) {
if (len == 1) {
*arr = 1;
return;
}
else if (*arr == 1) {
*arr = 0;//加一后变成零了
nums_add(arr + 1, len - 1);//让后面一位加一,然后剩余长度减一
}
else if(*arr==0){
*arr=1;//0加成1
}
}
void nums_add_(int* arr, int len) {
int k = len,i=0;
while (1) {
if (k == 1) {
arr[i] = 1;//如果长度为1了就退出
return;
}
if (arr[i] == 1) {
arr[i] = 0;
++i;
--k;
continue;//如果要进一我们还要循环一次,所以用continue
}
else if (arr[i] == 0) {
arr[i] = 1;
}
return;//到这里表示从0加到一,我们就不需要再循环了,直接结束循环
}
}
int main() {
int n = 0;
scanf("%d", &n);
int* arr = (int*)malloc(n * sizeof(int));
if (!arr)return -1;
for (int x = 0; x < n; ++x) {
scanf("%d", arr + x);
}
int* nums = (int*)calloc(n+1, sizeof(int));
int m[3];
while (1) {
nums_add_(nums, n + 1);
if (nums[n] == 1)break;
int k = 0;
for (int x = 0; x < n; ++x) {
if (nums[x] == 1)
{
if (k == 3)break;//已经有三个了还要存,直接跳过这个
m[k++] = arr[x];
}
}
if (k!=3)continue;//如果不等于三个,直接跳过到下一个循环
printf("%d %d %d",m[0],m[1],m[2]);
printf("\n");
}
return 0;
}
因为递归会开辟内存,所以后面的代码我们都用第二种非递归的
取出长度固定的所有子集
如果我们只要里面长度为3的子集怎么办呢?
自增变量来判断
我们可以在for循环里面先用一个长度为三的数组来存储我们的数据,再用一个变量来看是否满足。满足就打印。

在递归/非递归的时候就检测好
递归的时候我们完全就可以把1的数量统计好,所以可以做以下改变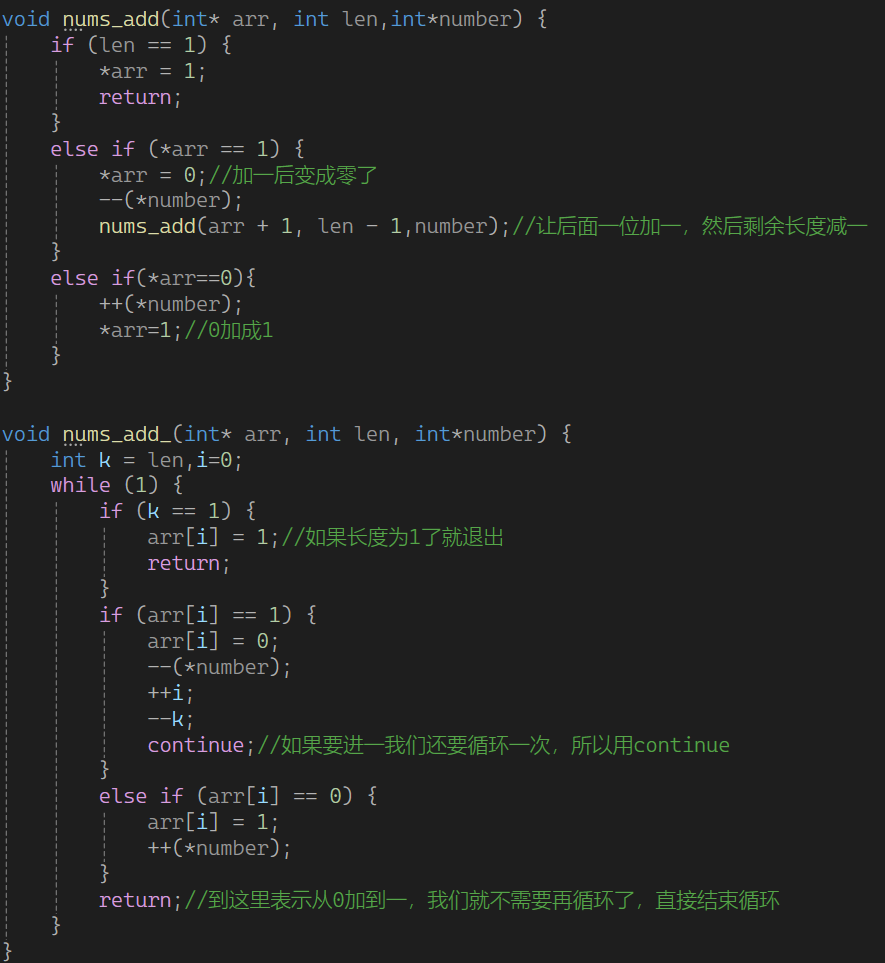

但是这样也没怎么变化嘛,那么我们既然可以知道1了,我们再储存一下有1的数组的位置可以吧?



这里我们发现是反着来的,我们把打印的顺序反过来就行了。因为这里的m数组相当于栈。
#include<stdio.h>
#include<stdlib.h>
void nums_add(int* begain_arr, int* arr, int* m, int* p, int len, int* number) {
if (len == 1) {
*arr = 1;
return;
}
else if (*arr == 1) {
*arr = 0;//加一后变成零了
--(*number);
if (*p>0) {
--p;
}
nums_add(arr,arr + 1,m,p, len - 1,number);//让后面一位加一,然后剩余长度减一
}
else if(*arr==0){
++(*number);
*arr=1;//0加成1
if (*p < 3) {
m[(*p)++] = (int)(arr - begain_arr);
}
}
}
void nums_add_(int* arr,int*m,int *p,int len, int*number) {
int k = len,i=0;
while (1) {
if (k == 1) {
arr[i] = 1;//如果长度为1了就退出
return;
}
if (arr[i] == 1) {
arr[i] = 0;
--(*number);
++i;
--k;
if (*p>0) {
--(*p);
}
continue;//如果要进一我们还要循环一次,所以用continue
}
else if (arr[i] == 0) {
arr[i] = 1;
++(*number);
if (*p < 3) {
m[(*p)++] =i;
}
}
return;//到这里表示从0加到一,我们就不需要再循环了,直接结束循环
}
}
int A_(int m, int n) {//非递归型
int k = 1, i = m, j = n;
while (1) {
if (i == 1)return k * j;
else {
k *= j;
--i;
--j;
}
}
}
int C_(int m, int n) {
return m == 0 ? 1 : A_(m, n) / A_(m, m);
}
int main() {
int n = 0;
scanf("%d", &n);
int* arr = (int*)malloc(n * sizeof(int));
if (!arr)return -1;
for (int x = 0; x < n; ++x) {
scanf("%d", arr + x);
}
int* nums = (int*)calloc(n+1, sizeof(int));
int m[3] , p = 0 , number1 = 0;//定义number1存储我们的1的数量
while (1) {
nums_add_(nums,m,&p, n + 1, &number1);
if (nums[n] == 1)break;
int k = 0;
if (number1 != 3)continue;
printf("%d %d %d",m[2],m[1],m[0]);
printf("\n");
}
return 0;
}
那么我们第一部分终于也是完成了,我嘞个豆真是多!!!!!!!!!!!!!!!!!!!!!!!!!
a,b的最小公倍数和最大公约数
我们题目要求的是最小公倍数,那么求这个我们可以枚举,但是时间复杂度复很高,所以我们就有特殊的算法。
我们首先要了解一个知识点就是
a*b=最大公约数(a,b)*最小公倍数(a,b)
我们求最小公倍数可能没有优秀的算法,但是我们最大公约数有优秀的算法。那么就可以通过这个式子进行转化。
辗转相除法求最大公约数
举个例子:求16 和 24的最大公约数
24%16 =8
16%8 = 0
所以答案是8
如果开始两个数字交换呢?
16%24=16
24%16=8
16%8=0
我们发现就是多了一部,没有太大差别。
那么我们开始实现
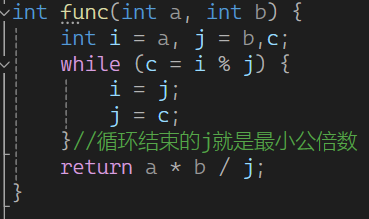
这里return的是最大公约数。
如果求三者的最大公约数或者最小公倍数,把其中两个数的先求出来,再看成整体和另一个求。
S
那么图中的表达式我们就可以算了
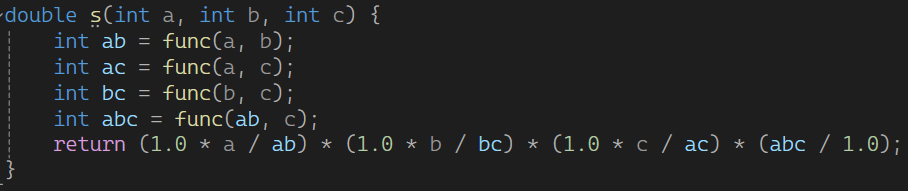
这里同样的,先除法再乘法,防止溢出了。
创建二维数组来存储三个都是1的数据。
我们就要用一个二维数组来储存我们的数据。那么每一个数组的长度是多少呢?
根据组合数我们要C(3,n)长度。排列组合在编程里面也很常见,我们也要知道他是怎么算出来的,排列组合我在下面讲到
排列组合函数
先是讲A(m,n)
如果m=n,那么就是算的阶乘。
我们可以通过A(m,n)=A(m-1,n-1)*n 来计算

C(m,n)
它有两个公式可以算,一个是C(m,n)=A(m,n)/A(n,n) 另一个是C(m,n)=n!/m!/(n-m)!
那么那个好呢?当然是第一个,第一个数字间相乘的次数少,不容易溢出。

储存后方便我们后面再取。
我们再用一个变量来存储S的最大值

那么我们的宝石问题就完成了。
真的完成了吗?
no no no
存储根本不需要二维数组,我写到这才发现,我们只要用一个长度为3个数组来储存最大的数据就行了
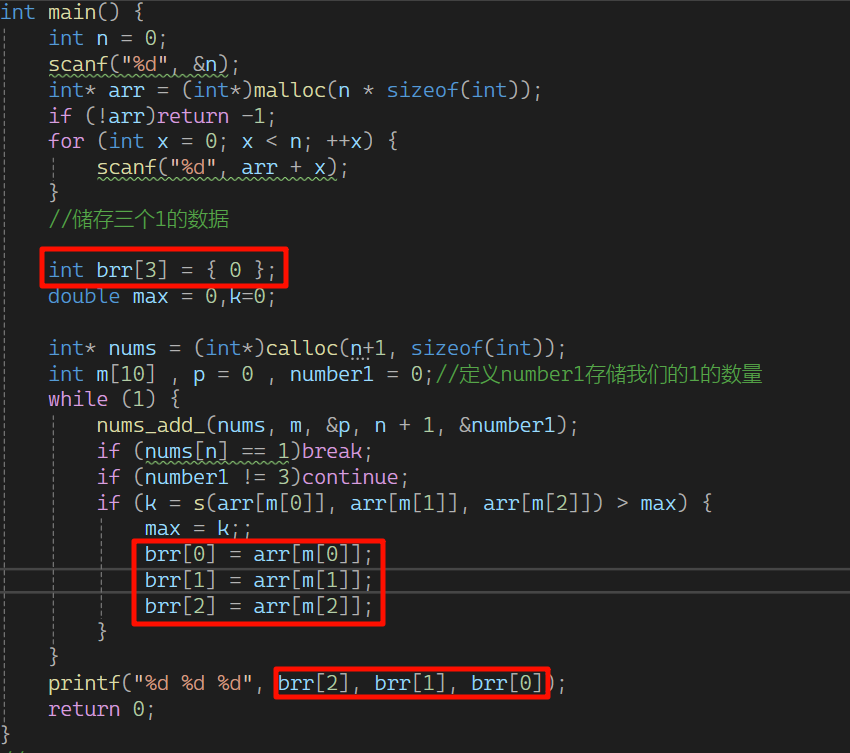
那么我们的排列组合函数就不需要了。
另外补充
我们m数组的长度定义的太短了,会产生越界访问。所以可以将m数组的长度定义长一点。可以和arr的数组一样长.
提前排序来解决字典序要求
我们的代码已经可以计算了,但是还有最后一个坑。例如我们逆向输入
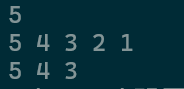
因为S(5,4,3)和S(1,2,3)的值是一样的,所以我们不会存后面字典序小的数据。我们最要先将数据进行排序。
这里我们光速搓一个快排出来

在计算之前排好序就行了。
最终的代码