简介

二叉树是一种常见的树形数据结构，它由节点组成，每个节点最多有两个子节点，分别称为左子节点和右子节点。这些节点以层次结构的方式组织在一起，每个节点都有一个父节点，除了根节点外，每个节点都有一个唯一的父节点。

二叉树具有以下特性：

1. 每个节点最多有两个子节点，分别为左子节点和右子节点。
2. 左子节点和右子节点的顺序不能颠倒，即左子节点必须在右子节点之前。
3. 二叉树的子树也是二叉树。

常见的二叉树类型包括：

• 二叉搜索树（Binary Search Tree，BST）：一种特殊的二叉树，其中每个节点的值都大于其左子树中的任何节点的值，且小于其右子树中的任何节点的值。
• 完全二叉树（Complete Binary Tree）：除了最后一层外，其他层的节点都被完全填充，并且最后一层的节点都集中在左侧。
• 平衡二叉树（Balanced Binary Tree）：树中任何节点的两个子树的高度差不超过1。

二叉树常用于实现搜索、排序和数据组织等算法。

创建

首先定义一个类来代表树中的结点，属性包括节点的值，它的左节点和右节点。

    /**
     * 定义二叉树
     */
    public static class TreeNode {
         int val;
         TreeNode left;
         TreeNode right;
         TreeNode() {}
         TreeNode(int val) { this.val = val; }
         TreeNode(int val, TreeNode left, TreeNode right) {
             this.val = val;
             this.left = left;
             this.right = right;
         }
    }

在主方法中创建几个节点，并将其连接起来。

    public static void main(String[] args) {
        TreeNode treeNode6 = new TreeNode(6);
        TreeNode treeNode5 = new TreeNode(5);
        TreeNode treeNode4 = new TreeNode(4);
        TreeNode treeNode3 = new TreeNode(3);
        TreeNode treeNode2 = new TreeNode(2);
        TreeNode treeNode1 = new TreeNode(1);

        treeNode1.left=treeNode2;
        treeNode1.right=treeNode3;
        treeNode2.left=treeNode4;
        treeNode2.right=treeNode5;
        treeNode3.left=treeNode6;
    }

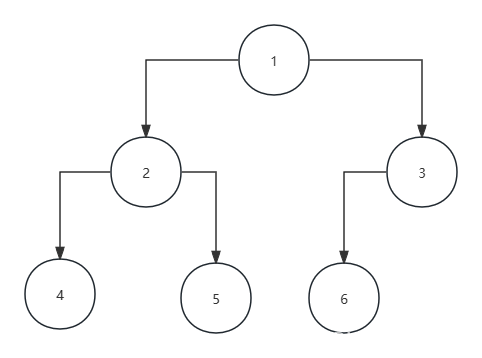
现在我们就得到了下图中的二叉树

广度优先搜索

上面二叉树广度优先搜索的结果为 1 2 3 4 5 6

所谓广度优先就是一层一层地遍历二叉树，在此不多做解释，具体解释可以查看我的另一篇博客

树的广度优先搜索（java实现）

深度优先搜索

树的深度优先搜索通常有三种方式，分别为先序，中序和后序。这三种方式都可以使用递归的方式实现和非递归的方式实现。

先序遍历

先序遍历（Pre-order Traversal）其遍历顺序为先访问根节点，然后依次递归地遍历左子树和右子树。

使用先序遍历上面二叉树得到的顺序为：1 2 4 5 3 6 

递归实现：

    /**
     * 递归实现先序遍历
     * @param root
     */
    public static void preOrder(TreeNode root){
        if(root==null) return;
        System.out.print(root.val+" ");
        preOrder(root.left);
        preOrder(root.right);
    }

非递归实现：

使用非递归主要时通过栈来实现，先将根节点放入栈中，随后进入循环，循环停止条件为栈空。在循环中，将刚放入栈的节点弹出，再将其左右节点压入栈，直到再无节点被压入栈，栈为空。这样就实现了先访问根节点，然后依次遍历左子树和右子树。

    /**
     * 非递归实现先序遍历
     * @param root
     */
    public static void preOrder2(TreeNode root){
        if (root == null)
            return;
        TreeNode c = new TreeNode();
        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);
        while (!stack.isEmpty()) {
            c = stack.pop();
            System.out.print(c.val + " ");
            if (c.right != null)
                stack.push(c.right);
            if (c.left != null)
                stack.push(c.left);
        }
    }

中序遍历

中序遍历（In-order Traversal）其遍历顺序为先递归地遍历左子树，然后访问根节点，最后递归地遍历右子树。

使用中序遍历上面二叉树得到的顺序为：4 2 5 1 6 3 

递归实现：

    /**
     * 递归实现中序遍历
     * @param root
     */
    public static void inOrder(TreeNode root){
        if(root==null) return;
        inOrder(root.left);
        System.out.print(root.val+" ");
        inOrder(root.right);
    }

非递归实现：

非递归实现中序遍历的方式也是使用栈，先将根节点压入栈，随后开始遍历，将其左子树压入栈，再将左子树的左子树压入栈，直到没有左子树为止。随后开始将刚才压入的节点弹出，每弹出一个，就去寻找其有物右子树，如果有右子树，就继续去遍历右子树的左子树。按照这样的规律一直遍历到栈为空就实现了中序遍历，先访问左子树，然后访问根节点，最后递归地遍历右子树。

    /**
     * 非递归实现中序遍历
     * @param root
     */
    public static void inOrder2(TreeNode root){
        TreeNode current = root;
        Stack<TreeNode> stack = new Stack<>();
        while (current != null || !stack.isEmpty()) {
            while (current != null) {
                stack.push(current);
                current = current.left;
            }
            if (!stack.isEmpty()) {
                current = stack.pop();
                System.out.print(current.val + " ");
                current = current.right;
            }
        }
    }

后序遍历

后序遍历（Post-order Traversal）其遍历顺序为先递归地遍历左子树，然后递归地遍历右子树，最后访问根节点。

使用后序遍历上面二叉树得到的顺序为：4 5 2 6 3 1 

递归实现：

    /**
     * 递归实现后序遍历
     * @param root
     */
    public static void postOrder(TreeNode root){
        if(root==null) return;
        postOrder(root.left);
        postOrder(root.right);
        System.out.print(root.val+" ");
    }

非递归实现：

非递归实现后续遍历依旧是使用栈来实现。但是想要实现需要两个栈来实现，一个栈用来改变记录改变当前的位置，一个栈用于记录下要遍历的结果。

先从根节点开始，一直遍历寻找其右子树，并将其压入两个栈中，当寻找到最下方时，将第一个栈中的节点弹出，弹出后会继续寻找该弹出节点的左子树，如果有继续压入两个栈中，如果没有则继续弹出。这样就最后的结果就存在第二个栈中，最后只需要将第二个栈中的节点依次弹出就得到了后续遍历的顺序，就实现了先递归地遍历左子树，然后递归地遍历右子树，最后访问根节点。

    /**
     * 非递归实现后续遍历
     * @param root
     */
    public static void postOrder2(TreeNode root){
        TreeNode current = root;
        Stack<TreeNode> stack1 = new Stack<>();
        Stack<TreeNode> stack2 = new Stack<>();
        while (current != null || !stack1.isEmpty()) {
            while (current != null) {
                stack1.push(current);
                stack2.push(current);
                current = current.right;
            }
            if (!stack1.isEmpty()) {
                current = stack1.pop();
                current = current.left;
            }
        }
        while (!stack2.isEmpty()) {
            System.out.print(stack2.pop().val + " ");
        }
    }