前言

上一节我们学习了链表的应用,那么这一节我们继续加深一下对链表的理解,我们继续通过Leetcode的经典题目来了解一下链表在实际应用中的功能,废话不多说,我们正式进入今天的学习
单链表相关经典算法OJ题4:合并两个有序链表
https://leetcode.cn/problems/merge-two-sorted-lists/description/
题目详情
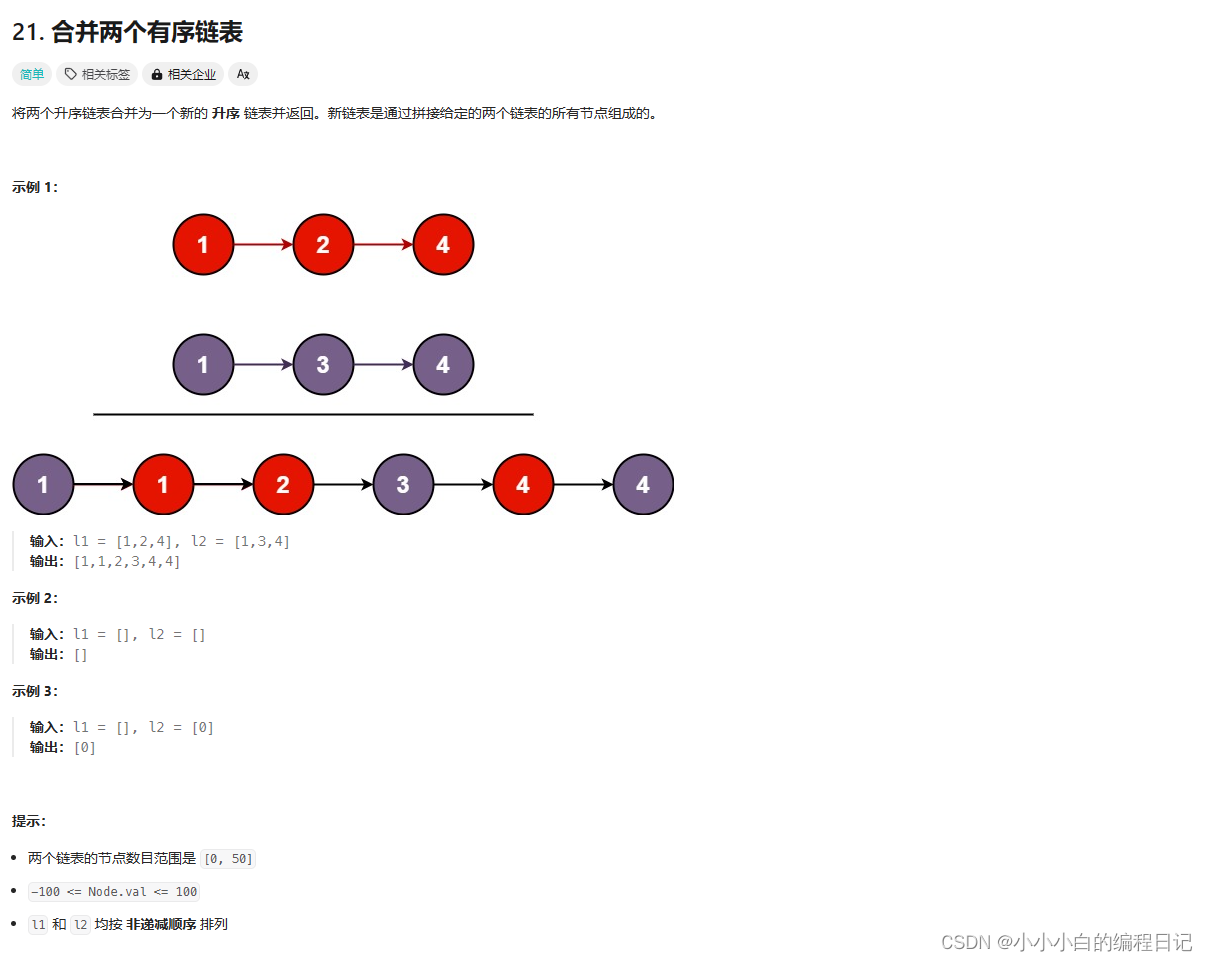
该题目与顺序表中的合并两个有序的数组的题目比较类似
题解
我们需要先创建一个新链表,用newHead和newTail分别指向链表的头和尾,再定义两个指针,l1指针用于第一个链表,l2指针用于第二个链表;
我们用l1指针指向的节点的数据大小和l2指针指向的节点的数据大小作比较,若
1.l1指向的节点的数据大于l2指向的节点的数据,则把l2指针指向的节点拿下来到一个新的链表尾插,再让l2指针执行++操作
2..l2指向的节点的数据大于l1指向的节点的数据,则把l1指针指向的节点拿下来到一个新的链表尾插,再让l1指针执行++操作
总的来说就是谁小就拿谁;
在我们遍历原链表的过程中,会存在两种结果:
1.l1为空,l2不为空
2.l2为空,l1不为空
我们在把第一个节点拿到新链表的时候,newHead和newTail都指向这一个节点,在这种情况下,该节点既为头也为尾
在我们继续向后拿入节点的时候,我们让newTail指向当前节点的位置,而newHead指针保持不动
以此类推,继续循环此操作,直到跳出循环,此时l1或者l2中的一个指针必定是走向了NULL指针
因为链表是升序的,我们此时只需要把没有走完的那个链表的剩余元素全部尾插到新链表就完成任务了
因为原链表可以为空。如果两个链表中的某个链表为空的话,可能就会存在对空指针的解引用,所以我们需要考虑空链表的问题;
根据上述我们梳理的条件,我们可以写出代码如下:
#define _CRT_SECURE_NO_WARNINGS 1
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
typedef struct ListNode ListNode;
struct ListNode* mergeTwoLists(struct ListNode* list1, struct ListNode* list2)
{
//判空
if (list1 == NULL)
{
return list2;
}
if (list2 == NULL)
{
return list1;
}
ListNode* l1 = list1;
ListNode* l2 = list2;
//创建的新链表
ListNode* newHead, * newTail;
newHead = newTail = NULL;
while (l1 && l2)
{
if (l1->val < l2->val)
{
//尾插l1
if (newHead == NULL)
{
newHead = newTail = l1;
}
else
{
newTail->next = l1;
newTail = newTail->next;
}
l1 = l1->next;
}
else
{
//尾插l2
if (newHead == NULL)
{
newHead = newTail = l2;
}
else
{
newTail->next = l2;
newTail = newTail->next;
}
l2 = l2->next;
}
}
//跳出循环后有两种情况:要么l1为空,要么l2为空
if (l2)
{
newTail->next = l2;
}
if (l1)
{
newTail->next = l1;
}
return newHead;
}我们此时在Leetcode的官网运行一下看看是否编写成功:

代码运行没有出现错误,编写成功
优化
我们重新审视一下代码,我们发现存在重复判断,我们每次拿下来节点的时候都需要对判断该节点是不是第一个节点的操作有些麻烦,会拖累程序的运行时间:
if (newHead == NULL)
{
newHead = newTail = l1;
}我们有没有什么办法优化一下呢?
这里代码存在重复的原因是因为:新链表是空链表,我们能不能让新链表不是空链表呢?这样就不需要重复的判断了,直接进行尾插就好了
因为刚开始创建新链表的时候,我们把newHead和newTail都设置成了空指针,此时我们可以让它动态申请一个空间,我们在这个新空间里不存储任何的数据
newHead = newTail = (ListNode*)malloc(sizeof(ListNode));此时的链表就不为空了,头尾指针都指向了一个有效的节点,只不过该节点里面没有存储任何的数据
该节点实际上是链表分类中的一种,叫做带头链表
在两个链表合并结束了以后,我们只需要将newHead的下一个节点返回就行就行
在进行优化后我们的代码如下:
#define _CRT_SECURE_NO_WARNINGS 1
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
typedef struct ListNode ListNode;
struct ListNode* mergeTwoLists(struct ListNode* list1, struct ListNode* list2)
{
//判空
if (list1 == NULL)
{
return list2;
}
if (list2 == NULL)
{
return list1;
}
ListNode* l1 = list1;
ListNode* l2 = list2;
//创建的新链表
ListNode* newHead, * newTail;
newHead = newTail = (ListNode*)malloc(sizeof(ListNode));
while (l1 && l2)
{
if (l1->val < l2->val)
{
//尾插l1
newTail->next = l1;
newTail = newTail->next;
l1 = l1->next;
}
else
{
//尾插l2
newTail->next = l2;
newTail = newTail->next;
l2 = l2->next;
}
}
//跳出循环后有两种情况:要么l1为空,要么l2为空
if (l2)
{
newTail->next = l2;
}
if (l1)
{
newTail->next = l1;
}
ListNode* ret = newHead->next;
free(newHead);
return ret;
}我们再检验一下代码是否正确:

代码没有错误,优化成功
循环链表经典应用-环形链表的约瑟夫问题
我们首先需要知道循环链表是什么东西
我们知道,链表的最后一个节点指向的是空指针NULL,而循环链表则不同,循环链表的最后一个节点指向的是该链表的第一个节点,这样就让链表成为了一个闭环
故事
著名的Josephus问题:据说著名犹太历史学家 Josephus 有过以下的故事:在罗⻢⼈占领乔塔帕特后,39个犹太⼈与 Josephus及他的朋友躲到⼀个洞中,39个犹太⼈决定宁愿死也不要被⼈抓到,于是决定了⼀个⾃杀⽅式,41个⼈排成⼀个圆圈,由第1个⼈开始报数,每报数到第3⼈该⼈就必须⾃杀,然后再由下⼀ 个重新报数,直到所有⼈都⾃杀⾝亡为⽌。 然⽽Josephus和他的朋友并不想遵从,Josephus要他的朋友先假装遵从,他将朋友与⾃⼰安排在 第16个与第31个位置,于是逃过了这场死亡游戏
题目详情

题解
我们首先需要定义两个指针prev和pcur,其中我们把pcur指针放在第一个节点的位置,让pcur指针去遍历链表,我们把prev指针放到循环链表的最后一个节点,prev指针也随着pcur指针的遍历而向后走,prev指针始终在pcur指针的后一位。(设m=5,n=2)

我们在遍历循环链表的时候,若是找到了顺序为n的节点,我们不能直接释放掉这一个节点,因为要是直接释放掉这个节点,那么顺序为n-1的节点就无法再找到顺序为n+1的节点并且连接起来。
当pcur指针找到了第n个节点时,我们让prev->next指向pcur的下一个节点,然后再把pcur释放掉。此时pcur已经变成了一个野指针,我们现在将pcur赋予原pcur的下一个结点的地址
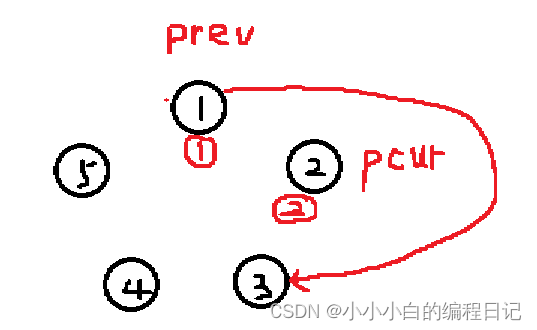
此时我们重新计数,当pcur再次找到顺序为n的节点时,重复执行之前的操作
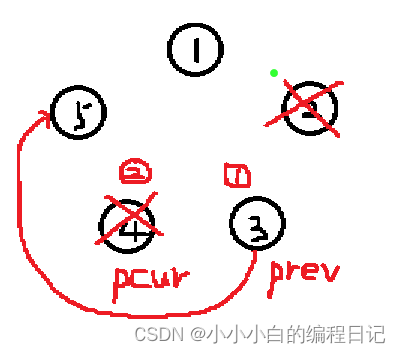
以此类推,直到原链表里面的节点个数小于n
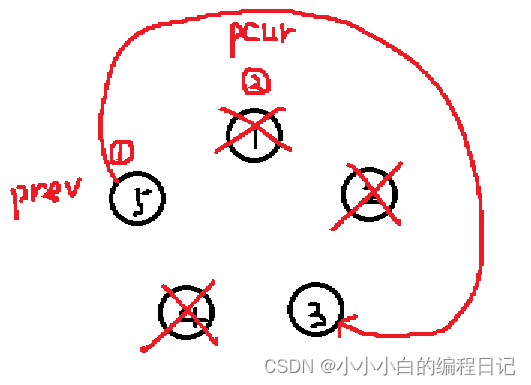

此时3的next指针指向了它本身
步骤1:创建带环链表
我们需要先创建头节点,然后根据步骤依次向下创建新的节点,我们首先封装一个函数应用于创建节点,该代码在链表专题中提及过,所以不再做过多的讲解:
//创建节点
ListNode* buyNode(int x)
{
ListNode* node = (ListNode*)malloc(sizeof(ListNode));
if (node == NULL)
{
exit(1);
}
node->val = x;
node->next = NULL;
return node;
}我们封装完创建节点的函数以后,紧接着封装一个创建带环链表的函数:
//创建带环链表
ListNode* creatCircle(int n)
{
//创建第一个节点
ListNode* phead = buyNode(1);
ListNode* ptail = phead;
//向后创建
for (int i = 2; i <= n; i++)
{
ptail->next = buyNode(i);
ptail = ptail->next;
}
//连接为闭环
ptail->next = phead;
return ptail;
}在该函数中,我们需要返回的是尾节点,因为若是n=1,则需要找到头节点的前一个元素;如果返回的是头节点,那么将找不到头节点之前的尾节点;
步骤2:遍历链表并且计数
在创建完带环链表之后我们需要遍历链表并且计数,此时我们需要创建一个count变量,count变量应该初始化为1
当count的取值等于n的时候,我们此时需要销毁pcur节点
在销毁pcur之前,我们需要先把prev和pcur指向的节点的下一个节点连接起来
根据这些推论,我们可以写出代码如下:
int ysf(int n, int m)
{
//根据n创建带环链表
ListNode* prev = creatCircle(n);
ListNode* pcur = prev->next;
int count = 1;
while (pcur->next != pcur)
{
if (count == m)
{
//销毁pcur节点
prev->next = pcur->next;
free(pcur);
pcur = prev->next;
count = 1;
}
else
{
//此时不需要销毁节点
prev = pcur;
pcur = pcur->next;
count++;
}
}
return pcur->val;
}此时我们的任务就完成了,我们看看代码是否正确:

代码成功运行
该题思路上难度并不大。但是我们要注意细节,不然很有可能会出现错误
单链表相关经典算法OJ题5:分割链表
https://leetcode.cn/problems/partition-list-lcci/
题目详情
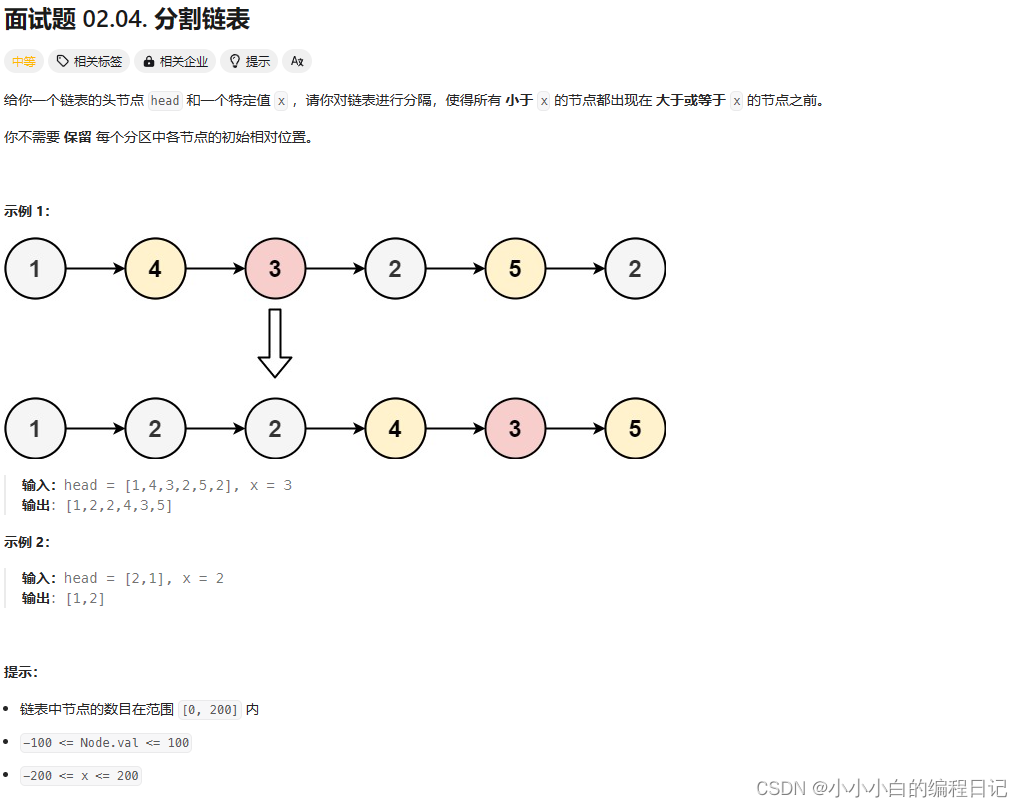
题解
方案一:(在原链表上进行修改)
我们定义一个指针pcur指向第一个节点,我们从第一个节点开始遍历;
如果我们遍历到小于3的节点,那么该节点就在原地保持不动;
若是遍历到了大于或者等于3的节点,那么我们先将该节点的前一个节点和后一个节点连接起来,再把该节点尾插到链表的末端;
当我们遍历完全链表的时候,我们的任务也就完成了;
因为该方法需要频繁的将节点断开、连接,而且需要使用多个指针(prev、pcur、ptail、phead)所以实现起来有点麻烦,一般不太推荐使用该方法
方案二:(在新链表上进行修改)
我们先定义pcur指针用来遍历原链表
我们动态申请一个哨兵位,并且定义两个变量newHead和newTail,将这两个变量都指向哨兵位;
若是pcur遍历的第一个节点的值小于x,则把该节点插到哨兵位后面,并且将newTail移动到该节点处;
若是pcur遍历的节点的值小于x,则把该节点头插到新链表中去;
若是pcur遍历的节点的值大于x,则把该节点尾插到新链表中去;
因为题目中说明了我们不需要保留每个分区中各个结点的初始相对位置,所以节点与节点之间的位置可以是随意的;
方案三:(小链表和大链表)
我们创建两个新链表,一个链表仅存放比x小的节点,另外一个链表仅存放比x大的节点;
在小链表中,我们创建两个变量lessHead和lessTail表示小链表的头和尾,我们此时动态申请一个哨兵位,里面不存放任何有效的值,若是原链表中的节点小于x,则该节点直接尾插到小链表中,并且让lessTail指向这个新插入的节点;
在大链表中,我们创建两个变量greaterHead和greaterTail表示小链表的头和尾,我们此时动态申请一个哨兵位,里面不存放任何有效的值,若是原链表中的节点大于x,则该节点直接尾插到小链表中,并且让greaterTail指向这个新插入的节点;
我们遍历完全链表时,大链表和小链表都已经全部插入完成了;
因为大小链表可以为空,我们需要进行判空操作,避免存在对空指针的解引用;
我们将小链表的尾节点和大链表的第一个有效的节点(不能和大链表的哨兵位连接在一起)首尾相连,这样我们就完成了任务;
首尾相连以后,如果大链表的尾节点不是原链表的尾节点,那么大链表尾节点指向的节点一定是一个小链表之中的节点,在我们代码运行的时候,大链表最后一个节点本来是应该指向空指针的,但是它不是原链表中的尾节点,例如代码示例中的5,它会指向小链表中的2,此时代码就会进入死循环,所以我们要考虑大链表的尾节点的指向是哪里,要手动把大链表尾节点指向NULL
我们再来考虑一下特殊情况:
若是原链表中只有一个数据1,那么大链表里面仅仅只有一个哨兵位,我们同样按步骤的思路去思考,发现仍然满足题意,所以代码不用进行修改
下面我们来试着实现该代码:
typedef struct ListNode ListNode;
struct ListNode* partition(struct ListNode* head, int x)
{
//判空
if (head == NULL)
{
return head;
}
//创建两个带头链表
ListNode* lessHead, * lessTail;
ListNode* greaterHead, * greaterTail;
lessHead = lessTail = (ListNode*)malloc(sizeof(ListNode));
greaterHead = greaterTail = (ListNode*)malloc(sizeof(ListNode));
//遍历原链表,将原链表的节点尾插到大小链表中
ListNode* pcur = head;
while (pcur)
{
if (pcur->val < x)
{
//尾插到小链表
lessTail->next = pcur;
lessTail = lessTail->next;
}
else
{
//尾插到大链表中
greaterTail->next = pcur;
greaterTail = greaterTail->next;
}
pcur = pcur->next;
}
//处理大链表尾节点next指针指向+next指针初始化
greaterTail->next = NULL;
//小链表大链表首尾相连
lessTail->next = greaterHead->next;
//释放
ListNode* ret = lessHead->next;
free(lessHead);
free(greaterHead);
lessHead = greaterHead = NULL;
return ret;
}我们试着运行一下代码:

代码成功运行,编写成功
结尾
本节我们同样是学习链表的应用,通过这两节的学习,我们对链表的理解更加深入了,那么关于链表的所有内容到了本节为止就暂时告一段落了,下一节我们将学习双向链表,谢谢您的浏览!!!