1 基本概念

1.1 欧拉路径和欧拉回路

欧拉路径：欧拉路是指从图中任意一个点开始到图中任意一个点结束的路径，并且图中每条边通过的且只通过一次。
欧拉回路:欧拉回路是指起点和终点相同的欧拉路。
注意：如果欧拉回路，那么一定存在欧拉路径

注意： 是每条边被访问一次，节点可能会被访问两次。

充分必要条件：
对于无向图，所有边都是连通的

（1）存在欧拉路径的充分必要条件：

• 度数为奇数的点只能是0个或者2个

（2）存在欧拉回路的充分必要条件：

• 度数为奇数的只能是0个

对于有向图，所有边都是连通的

（1）存在欧拉路径的充分必要条件：

• 要么所有点的出度均等于入度。
• 要么除了两个点之外，其余所有点的出度等于入度，剩余的两个点：一个满足出度比入度多1（起点），另一个满足入度比出度多1（终点）。

（2）存在欧拉回路的充分必要条件：

• 所有点的出度均等于入度

2 欧拉路径判定算法

2.1 Fleury(弗罗莱) 算法

Fleury算法用来判断图是否是欧拉路径或欧拉回路的算法。
使用如下的欧拉图，了解Fleury算法的主要步骤。

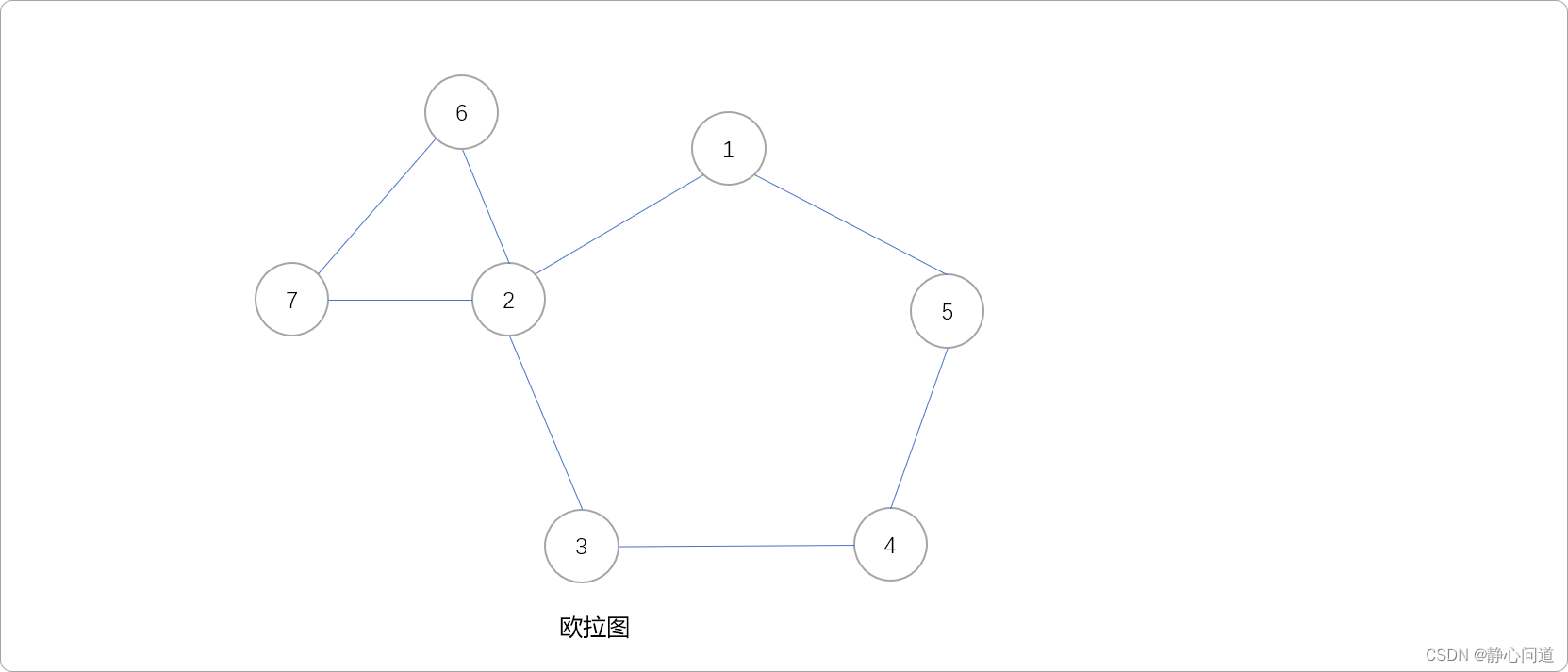
• 选节点1为起点，并将该起点加入路径中。Fleury算法选择栈存储欧拉路径。
  
• 从起点开始，一路DFS试着走出一条通路。方法是找与此节点相邻的节点。
  如果只有一个节点，则将这个点直接加入路径中。
  如果有多个相邻节点，则选择其中一条边，把相邻节点加入路径后，且删除这一条边。
  如果没有邻接节点，则从路径中弹出。
  节点5和节点2都与1相邻，可以选择向5方向，也可以选择2方向。这里选择2方向，把节点2放入路径，然后置1-2这条边为删除状态。如此这般，一路经过3、4、5节点后回到1号节点。下图中标记为红色的边表示已经访问或被删除。
  
• 重新回到节点1，此时不再存在与节点1邻接的节点，从路径中弹也，依次可弹出5、4、3。直到碰到2号节点。
  
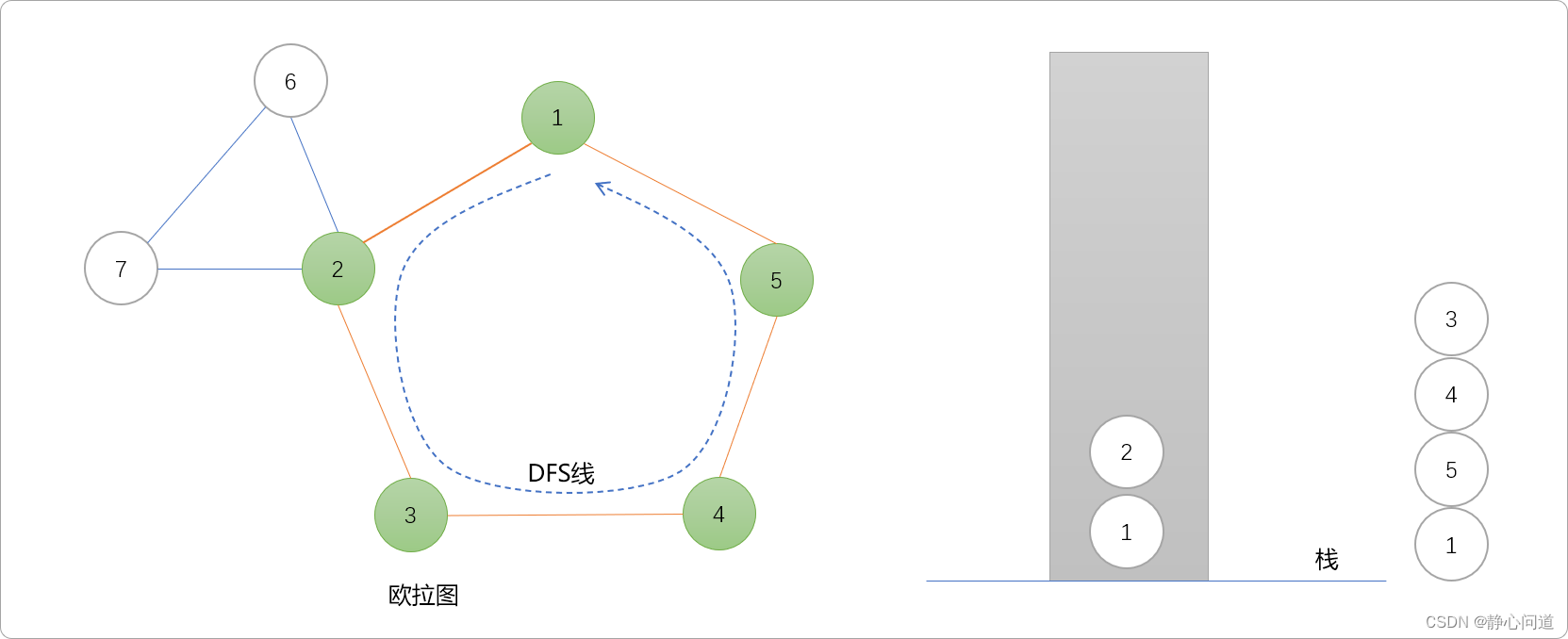
• 因为存在与2号节点邻接的节点，再次以2号节点为始点，使用DFS开路。一路上遇到6、7，且再次回到2号节点。
  
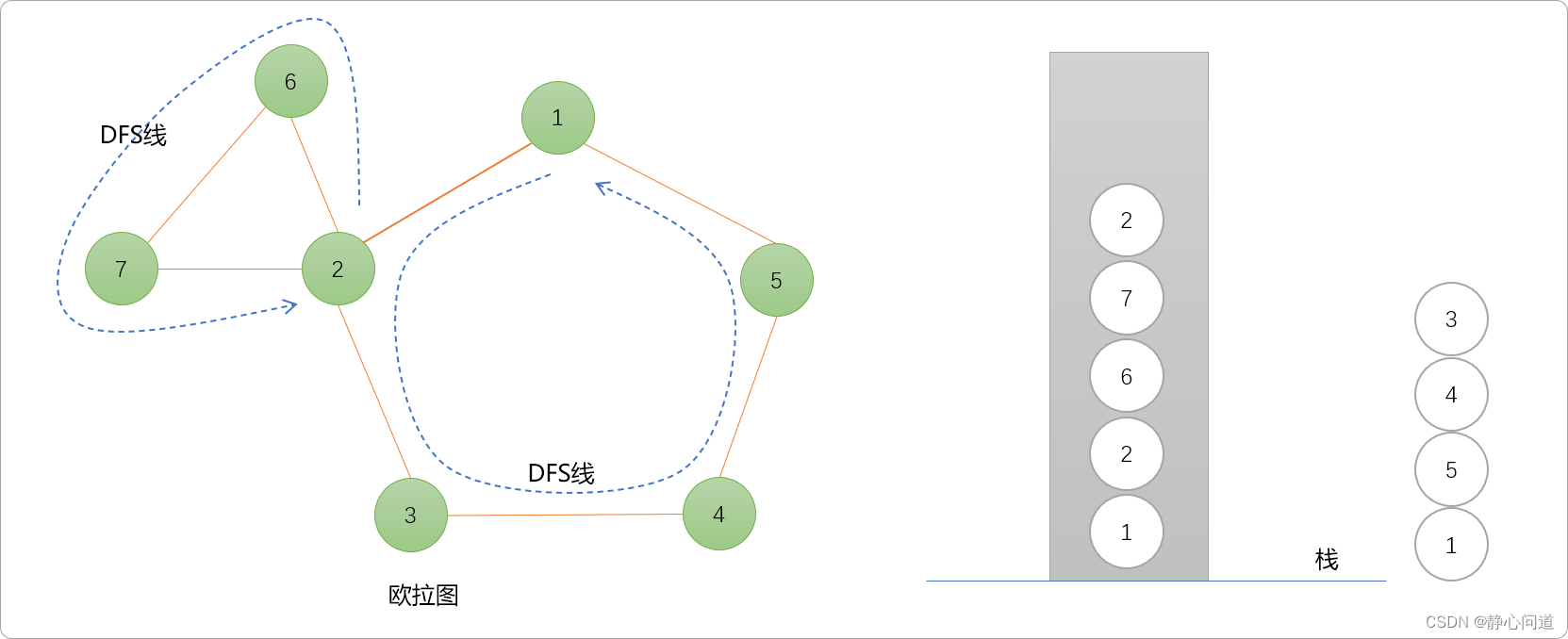
• 2号节点不存在与之邻接的节点，出栈。同理，7、6依次出栈。
  
  小结：
  当有与当前节点邻接的节点时，一路DFS，直到没有邻接的尽头。些时，一轮DFS算法结束，从路径中依次弹出没有邻接节点的节点，直到遇到还有邻接节点的节点，新一轮的DFS重新开始。直到所有节点邻接的边全部访问完毕。
  编码实现：

#include <iostream>
#include <math.h>
#include <algorithm>
#include <cstring>
#include <stack>
#define INF 100000
using namespace std;
int graph[100][100];
int n,m;
stack<int> sta;
void read() {
	for(int i = 0; i < m; i++) {
		int f,t;
		cin >> f >> t;
		graph[f][t] = 1;
		graph[t][f] = 1;
	}
}
void dfs(int u) {
	sta.push(u);
	for(int i = 1; i <= n; i++) {
		if(graph[i][u] > 0) {
			//标记为删除
			graph[u][i] = 0;
			graph[i][u] = 0;
			dfs(i);
			//仅朝一条边方向 DFS,方便形成回路 
			break;
		}
	}
}
void fleury(int x) {
	int  isEdge;
	sta.push(x);
	while(!sta.empty()) {
		isEdge = 0;
		int t = sta.top();
		sta.pop();
		//检查是否有边
		for(int i = 1; i <= n; i++) {
			if(graph[t][i] > 0) {
				isEdge = 1;
				break;
			}
		}
		if(isEdge == 0) {
			//没有邻接边，输出
			cout << t << " ";
		} else {
			//有邻接边，一路DFS狂奔
			dfs(t);
		}
	}
}
int main() {
	cin >> n >> m;
	memset(graph,0,sizeof(graph));
	read();
	int num = 0;
	int start = 1;
	for(int i = 1; i <= n; i++) {
		int deg = 0;
		for(int j = 1; j <= n; j++)
			deg += graph[i][j];
		if(deg % 2 == 1) {
			//奇节点的数量
			start = i;
			num++;
		}
	}
	if(num == 0 || num == 2)
		fleury(start);
	else
		cout << "不存在欧拉路径" << endl;
	return 0;
}
//测试用例
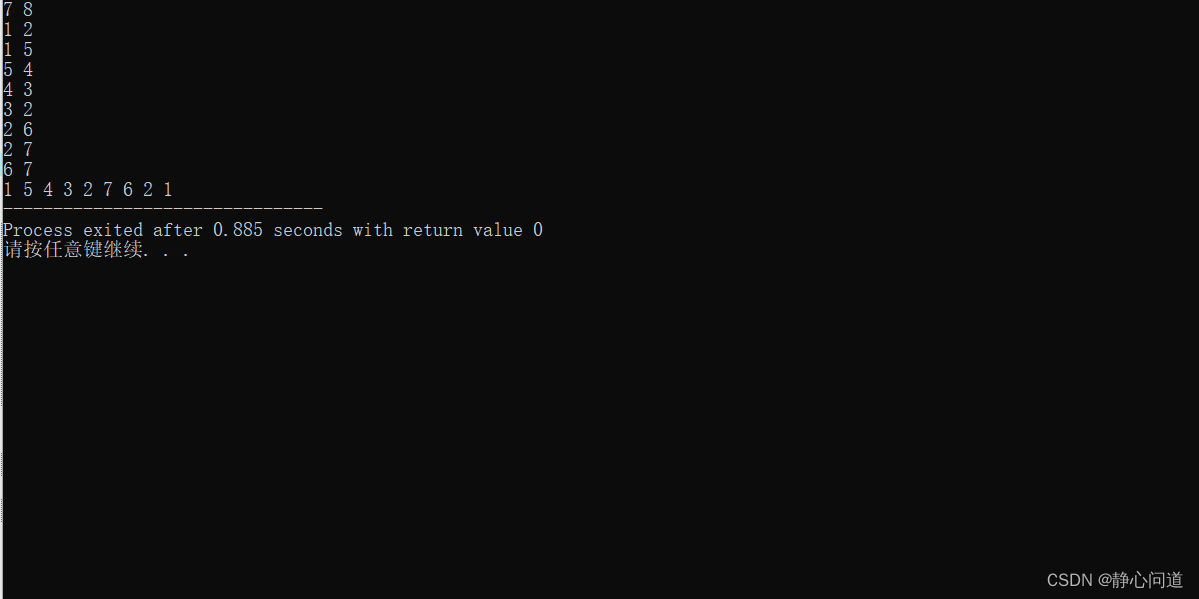
7 8
1 2
1 5
2 3
2 6
2 7    
3 4
4 5
6 7    

测试结果

from typing import List
from collections import defaultdict


class Solution:
    def __init__(self):
        self.G = defaultdict(list)
        self.degree = defaultdict(int)
        self.res = []
        
    def dfs(self, start):
        for j in self.G[start]:
            if j in self.G[start]:
                self.G[start].remove(j)
                self.G[j].remove(start)
                self.dfs(j)
        self.res.append(start)


    def fleury(self, connects) -> List:
        for con in connects:
            self.G[con[0]].append(con[1])
            self.degree[con[0]] += 1
            self.G[con[1]].append(con[0])
            self.degree[con[1]] += 1
        start = connects[0][0]
        cnt = 0
        for k,v in self.degree.items():
            if v %2 != 0:
                cnt += 1
                start = k
        if cnt == 0 or cnt == 2:
            self.dfs(start)
        else:
            print("不存在欧拉路径")
            return []
        return self.res
        

if __name__ == "__main__":
    so = Solution()
    connects = [[1,2], [2,3], [3,4],[4,5],[5, 1],[2,6],[6,7],[7,2]]
    res = so.fleury(connects)
    print(res)
        

2.2 Hierholzer 算法

也称逐步插入回路法。由数学家卡尔·希尔霍尔策给出，基于贪心思想。Hierholzer 的基本思路。先找到一个子回路，以此子回路为基础，逐步将其它回路以插入的方式合并到该子回路中，最终形成完整的欧拉回路。继续使用上图做演示。

• 寻找子回路：如下从节点1开始，沿着边遍历图，一边遍历一边删除经过的边。如果遇到一个所有边都被删除的节点，那么该节点必然是 1（回到初始点）。将该回路上的节点和边添加到结果序列中。这个过程和Fleury算法没有太多区别。
  

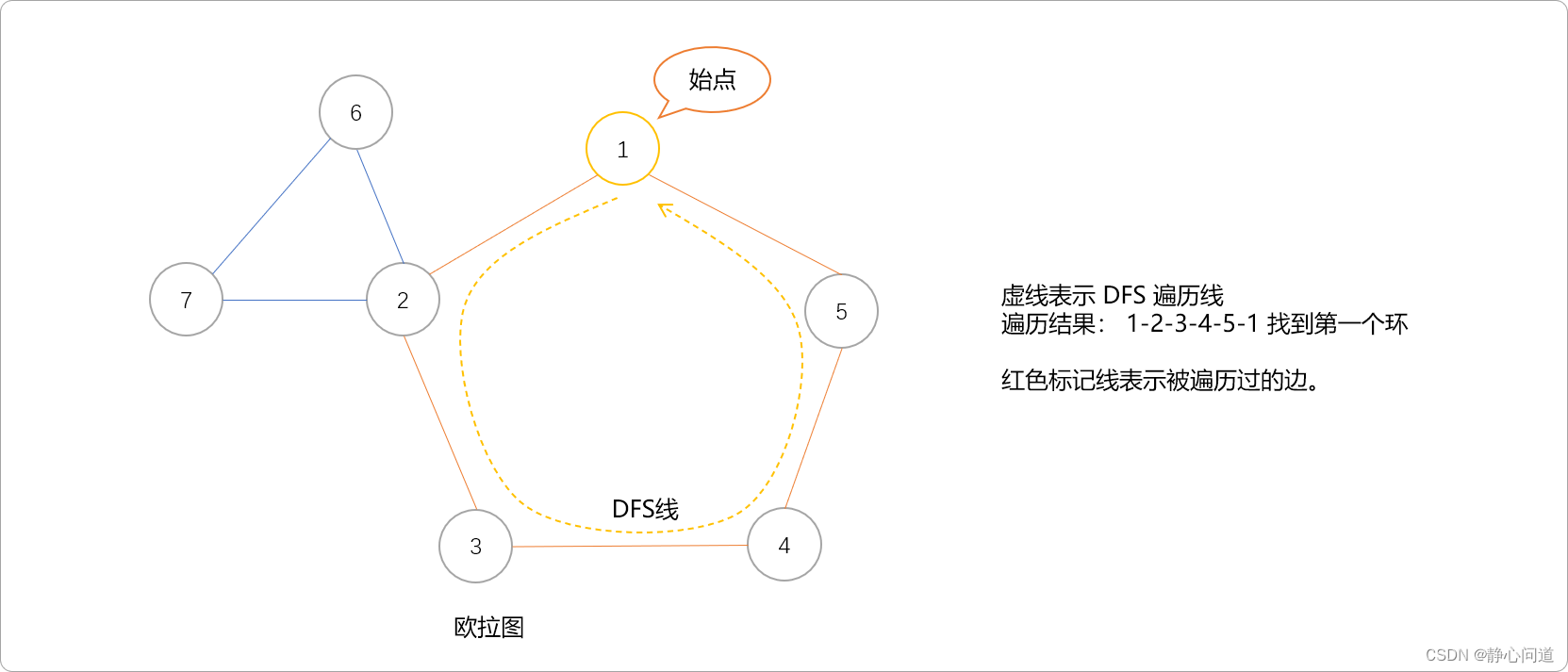
• 回溯时检查刚添加到结果序列中的节点，看是否还有与节点相连且未遍历的边。可发现节点 2 有未遍历的边，则从 2 出发开始遍历，找到一个包含2 的新回路，将结果序列中的一个 2 用这个新回路替换，此时结果序列仍然是一个回路。这是和Fleury算法最大区别。
  

• 重复直到所有边都被遍历。

编码实现：

#include<iostream>
#include<string.h>
#include<vector>

const int maxn = 10005;
const int maxm = 1000005;//edge
using namespace std;
int n,m;
struct Edge {
	int to, nxt;
	bool vis=0;
};
Edge edge[maxm];
//如果没有以 i 为起点的有向边则 head[i] 的值为 0
int head[maxm];
//边的个数
int cnt;
//存储找到的回路
vector<Edge> ans;
//起始点
int sn;

void init() {
	for(int i=1; i<=n; i++) {
		head[i]=0;
		cnt=0;
	}
}

/*
*添加边
*/
void addEdge(int from, int to) {
	edge[cnt].to = to;
	edge[cnt].nxt = head[from];
	head[from] = cnt++;
}
void read() {
	int f,t;
	for(int i=1; i<=m; i++) {
		cin>>f>>t;
		addEdge(f,t);
		addEdge(t,f);
	}
}
void hierholzer(int sn) {
	for (int i = head[sn]; i != 0; i = edge[i].nxt) {
		// 遍历过
		if (edge[i].vis) continue;
		// 删除
		edge[i].vis = edge[i ^ 1].vis = true;
		// 继续
		hierholzer(edge[i].to);
		// 回溯时加入结果序列后，循环会继续查找是否有邻接边
		ans.push_back(edge[i]);
        
	}
}
void show() {
	for(int i=0; i<ans.size(); i++) {
		cout<<ans[i].to<<"\t";
	}
	cout<<sn<<"\t";
}

int main() {
	cin>>n>>m;
	sn=1;
	init();
	read();
	hierholzer(sn);
	show();
	return 0;
}

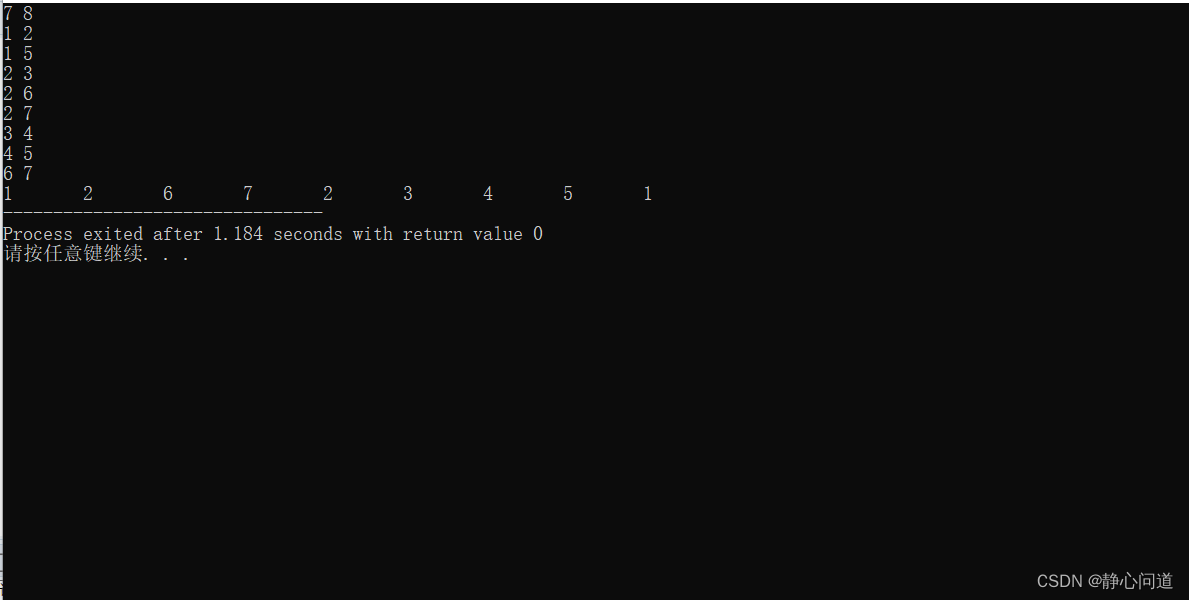
测试结果：

3. 总结

Hierholzer和Fleury算法的基本思路差不多，在DFS时找环。Fleury使用分段策略，找到一条环后，以环中某一个还存在邻接边的节点重新开始使用DFS找环，直到找到所有环。Hierholzer算法很有技巧性，在回溯时检查节点是否还有邻接边，有则重新DFS直到完毕。

参考资料：
https://blog.csdn.net/y6123236/article/details/135020029
https://blog.csdn.net/binggui2/article/details/108540016