A:

买n个酸奶，一次一瓶a元,一次买两瓶可以优惠价b元,也可以a元,问恰好买n瓶需要多少钱.

void solve() {
    int n, a, b;
    cin >> n >> a >> b;
    int ans = min(a * n, n / 2 * b + n % 2 * a);
    cout << ans << endl;
}

B:

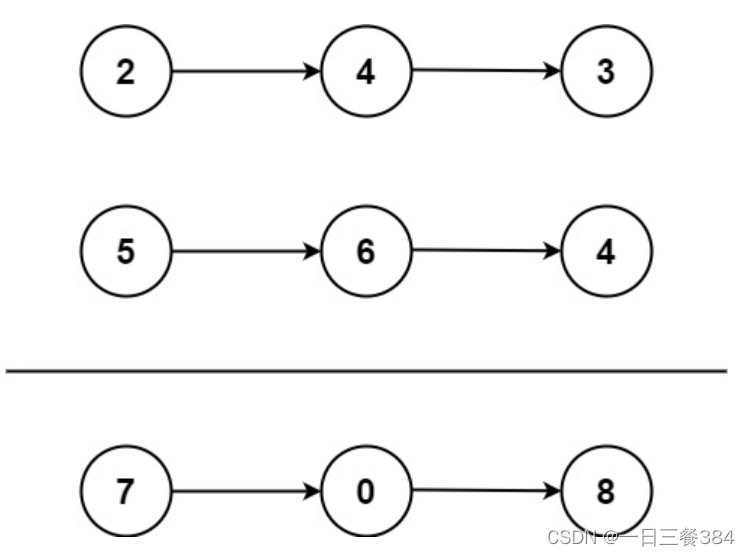
给你一个数组,问能否构造出下图的东西.

此题c,b皆为正数,所以左上角数字肯定是排序后的第一个数字.

然后去构造出:

存到数组,排序,判断是否相等

void solve() {
    int n, c, d;
    vector<int>a;
    cin >> n >> c >> d;
    for (int i = 1; i <= n * n; i++) {
        int x; cin >> x;
        a.push_back(x);
    }sort(a.begin(), a.end());
    int p = a[0];
    vector<int>b;
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            int x = p + i * c + j * d;
            b.push_back(x);
        }
    }sort(b.begin(), b.end());

    if (a == b)cout << "YES" << endl;
    else cout << "NO" << endl;
}

C:

 先从左边攻击,所以左边的攻击次数是

右边攻击次数

去从左边开始枚举,如果小于等于攻击次数,ans++,同时攻击次数减去a[i],再把a[i]设置为1e18,避免从右边又计算一次.否则a[i]大于攻击次数,a[i]-=L.退出.

从右边做一次即可.

void solve() {
    int n, k; cin >> n >> k;
    vector<int>a(n + 1); int ans = 0;
    for (int i = 1; i <= n; i++)cin >> a[i];
    int L = (k + 1) / 2;
    int R = (k / 2);
    for (int i = 1; i <= n; i++) {
        if (a[i] <= L) {
            ans++; L -= a[i]; a[i] = 1e18;
        }
        else {
            a[i] -= L;
            break;
        }
    }
    for (int i = n; i >= 1; i--) {
        if (a[i] <= R) {
            ans++; R -= a[i];
            a[i] = 1e18;
        }
        else {
            cout << ans << endl;
            return;
        }
    }cout << ans << endl;
}

D:

D一开始我外层循环,内层双指针T了,看来是个滑动窗口的思想

void solve() {
    int n, m, k; cin >> n >> m >> k;
    vector<int>a(n + 1);
    vector<int>b(m + 1);
    int ans = 0; int now = 0;
    for (int i = 1; i <= n; i++)cin >> a[i];
    for (int j = 1; j <= m; j++)cin >> b[j], c[b[j]]++;//c数组记录b[j]出现的次数
    for (int i = 1; i <= n; i++) {
        //如果a[i]在c中不为0(既b数组中出现过)
        //并且a[i]这个数字在d这个窗口的出现次数小于
        //now++
        if (c[a[i]]&&d[a[i]] < c[a[i]]) {
            now++;
        }
        //进来一个
        d[a[i]]++;
        
        //窗口长度为m i-m>=1 表示肯定要弹出一个了
        if (i - m >= 1) {
            //左边弹出
            d[a[i - m]]--;

            //[1 2 3] 4---->1 [2 3 4]
            //1 2 3
            //例如这个例子 1弹出 所以这个窗口1的数量小于c数组 配对数字--
            if (d[a[i - m]] < c[a[i - m]])now--;
        }
        //i>=m是因为题目要求窗口必须m的大小 显然i在m之前无法形成大小为m的窗口(i是右端点)
        if (i >= m && now >= k)ans++;
    }cout << ans << endl;
    //注意这里只需要把有值的清空 不然1e6TLE
    for (int i = 1; i <= n; i++) {
        d[a[i]] = 0;
    }
    for (int i = 1; i <= m; i++) {
        c[b[i]] = 0;
    }
}

F:

有1,2,3,4,四个数字,输入四个数字的个数,如果异或和等于0,则Bob获胜,每次游戏结束,可以删去掉一个数字,继续游戏,直到为空.

例如2 2 2 0这个例子,不操作赢一次,0 2 2 0两次,0 0 2 0三次.结束

请注意:是不可以0 0 0 0

题意纯属nt:比如2 2 2 0这个例子,Bob胜利有以下情况

2 2 2 0,0 2 2 0,0 0 2 0    

2 2 0 0,0 2 0 0,2 0 0 0

这样理解是错误的,此题不是说Bob有几种胜利的方式,而是在一局游戏中,最优操作得到的胜利次数.

比如上面的[0 2 2 0]和[2 2 0 0]在一局游戏中是不能都得到的.因为这是一局游戏,如果得到[0 2 2 0]就必须删除一号位的数字,那么一号位的数字被删除,又怎么能得到[2 2 0 0]呢？

可以单独考虑每个数字,例如[5 0 0 0]答案显然是2。

可以得知ans+=pi/2

但是可能[1 1 1 0],[5 3 3],这种本来就是异或为0,共同特征是a*b*c%2==1

void solve() {
	int a, b, c, d; 
	cin >> a >> b >> c >> d;
	int ans = 0;
	ans += a / 2 + b / 2 + c / 2 + d / 2 + a * b * c % 2;
	cout << ans << endl;
}