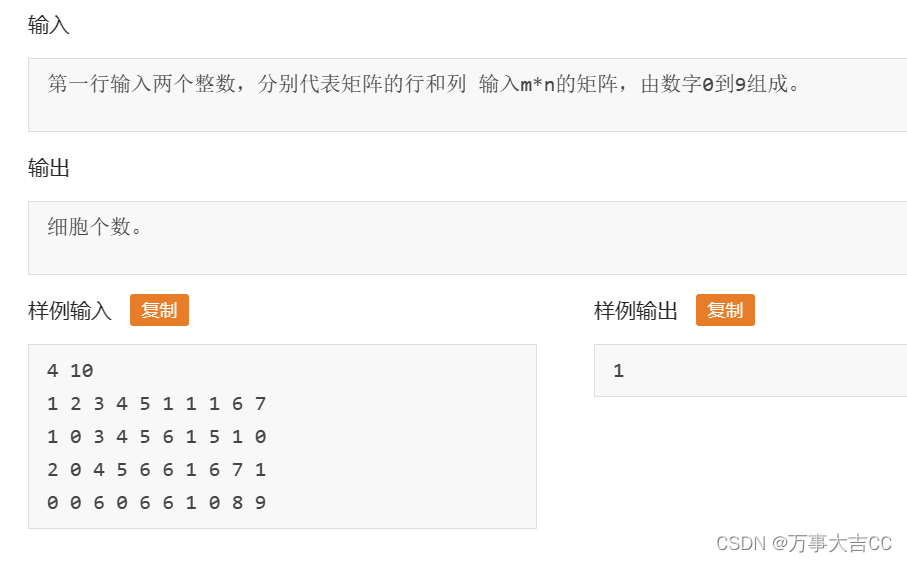
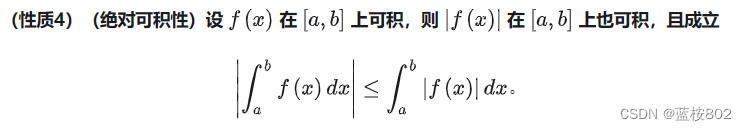1.一元微分学的概念和一元积分学的概念

一元微分

1.导数

函数一点可导的充要条件：左右导数均存在且相等（也可说左右极限存在且相等）

函数一点可导的必要条件：若f(x)在一点可导，则f(x)在该点连续。反之未必。

2.导数的几何意义

函数y=f(x) 在x=x0处的导数 f′(x0)，表示曲线y=f(x)在点P(x0,f(x0))处的切线的斜率k。

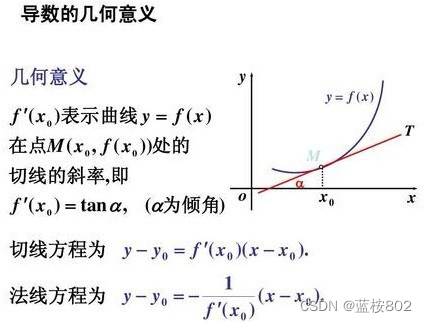
注意：一点的导数存在-->该点切线存在，但反之不能推。例如：y=|x|;

3.高阶导数

4.微分的概念

微分是一个变量在某个变化过程中的改变量的线性主要部分。若函数y=f(x)在点x处有导数f'(x)存在，则y因x的变化量△x所引起的改变量是△y=f(x+△x)一f(x)=f'(x)·△x+o(△x)，式中o(△x)随△x趋于0。因此△y的线性形式的主要部分dy=f'(x)△x是y的微分。 [6]可见，微分作为函数的一种运算，是与求导（函）数的运算一致的。

可微与可导的关系

可微的几何意义

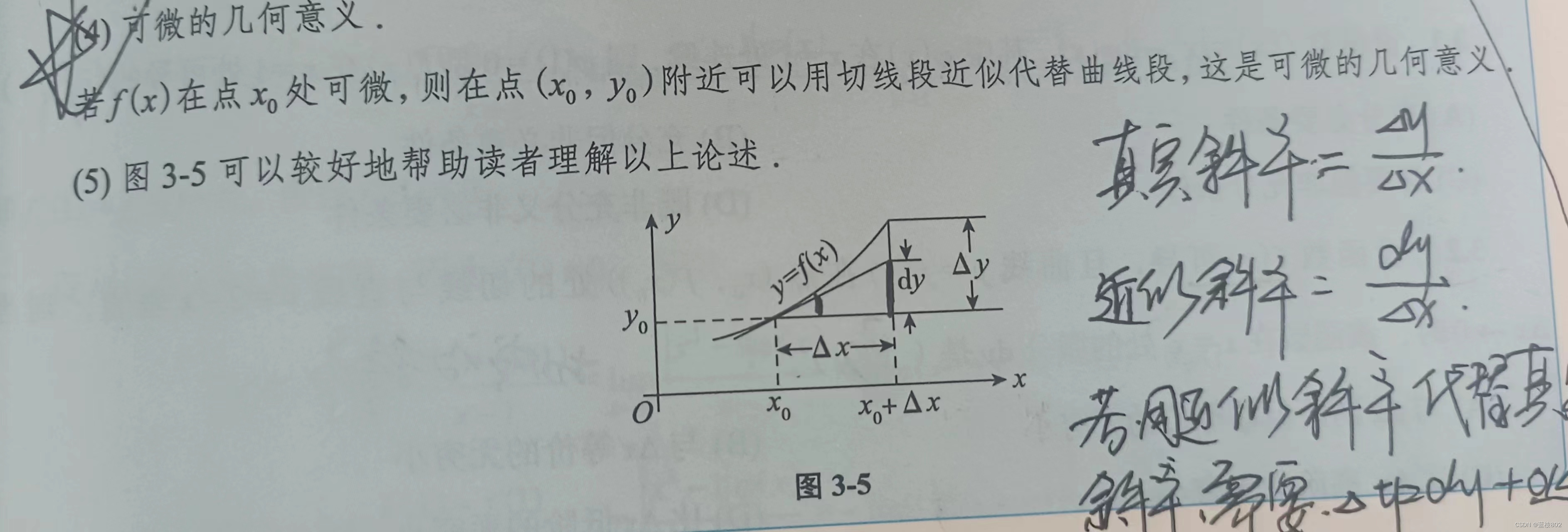
2.一元积分学

1.不定积分（求解原函数的过程）

原函数不唯一，其差别在于C（常数）

原函数存在i定理

（1）连续函数f(x)必有原函数F(x)；

（2）含有第一类间断点和无穷间断点的函数f(x)在包含该间断点的区间内必没有原函数F(x)；（有振荡间断点的f(x)可能有原函数也可能没有）

2.定积分（微分法）

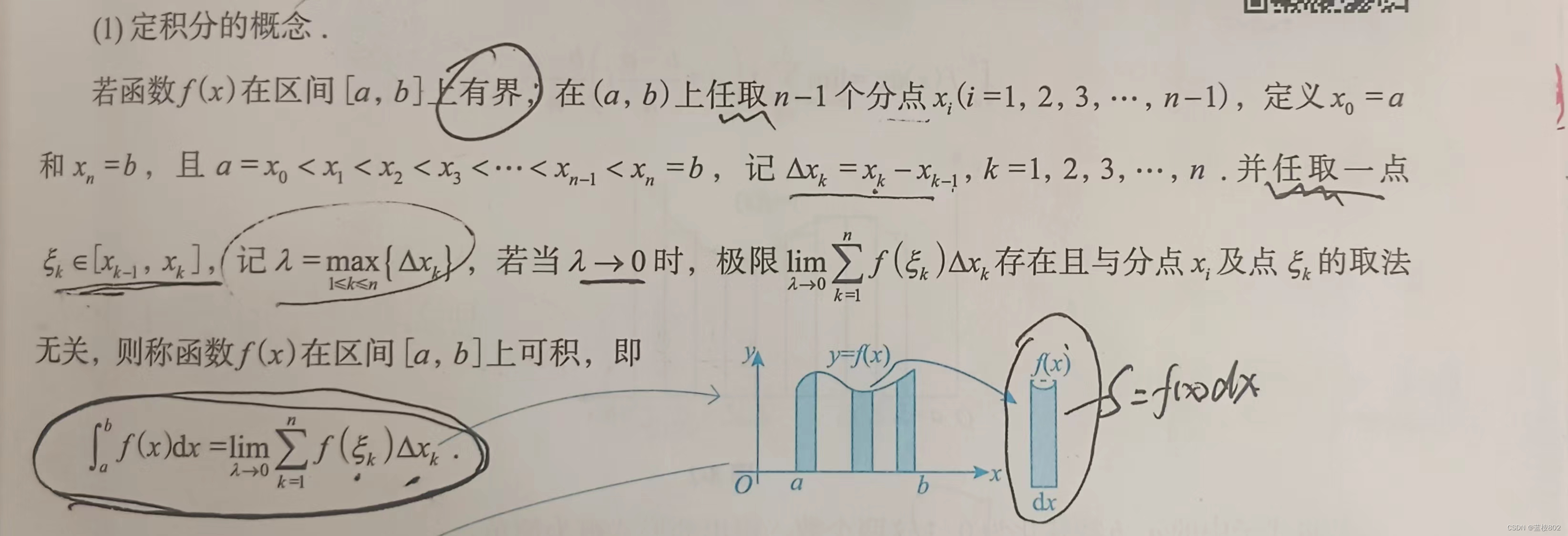
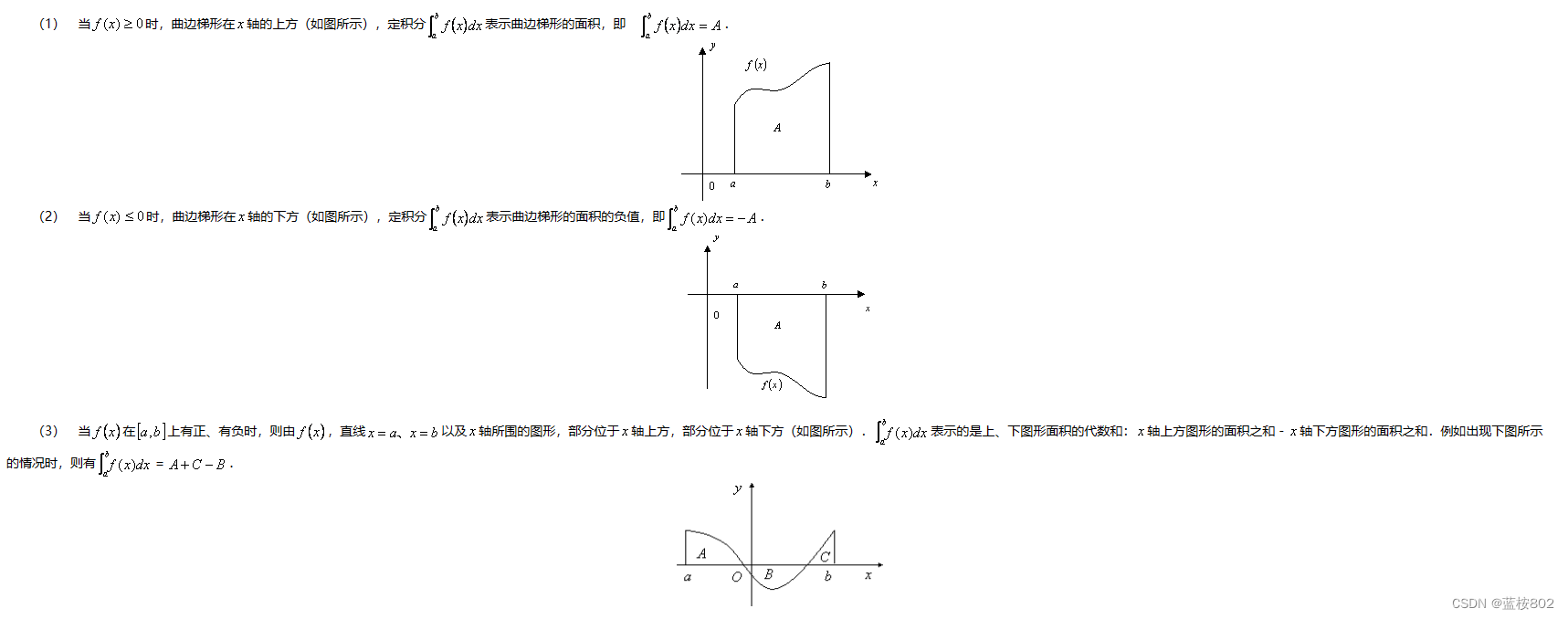
几何意义

定积分存在定理

（1）充分条件：若f(x)在[a,b]上连续，则定积分存在；若f(x)在[a,b]上单调，则定积分存在；若f(x)在[a,b]上有界且只有有限个间断点，则定积分存在；

（2）必要条件：可积函数必有界

定积分的性质：