题目1 392 判读子序列
题目链接 392 判断子序列
题意
判断字符串s是否为字符串t的子序列 (子序列的相对位置在原字符串中不改变)
就是求最长公共子序列的长度与字符串s的长度是否相等
动态规划
1)确定dp数组及下标i的含义
dp[i][j] 表示以s[i-1]结尾的字符串与以t[j-1]结尾的字符串公共序列的最大长度
2)dp数组初始化
根据递推公式 dp[0][1] = 0 dp[1][0] = 0
3)递推公式
if(s[i-1] == t[j-1]) dp[i][j] = dp[i-1][j-1] +1;
else dp[i][j] = dp[i-1][j]; 考虑1种情况 删除t字符串中该位置的元素(减1),该位置元素对应不等
4)遍历顺序
根据递推公式 从前向后遍历 从左向右遍历
for(int i =1; i <= s.size(); i++){
for(int j = 1; j <= t.size(); j++){
}
}

5)打印dp数组
代码
class Solution {
public:
bool isSubsequence(string s, string t) {
if(s.size() > t.size()) return false;
int result = 0;
//定义dp数组 初始化
vector<vector<int>> dp(s.size() + 1, vector<int>(t.size() + 1, 0));
for(int i = 1; i <= s.size(); i++){
for(int j = 1; j <= t.size(); j++){
if(s[i-1] == t[j-1]) dp[i][j] = dp[i-1][j-1] + 1;
else dp[i][j] = dp[i][j-1];
result = max(result, dp[i][j]);
}
}
if(result == s.size()) return true;
return false;
}
};- 时间复杂度:O(n × m)
- 空间复杂度:O(n × m)
题目2 115 不同的子序列
题目链接 115 不同的子序列
题意
统计字符串s的子序列中字符串t出现的次数 即字符串s里面删除t能否变成字符串t
动态规划
1)确定dp数组及下标i的含义
dp[i][j] 以s[i-1]为结尾的字符串s中有t[j-1]为结尾的字符串t的个数
2)dp数组初始化
根据递推公式 dp[i][0]=1 字符串s中有1个空字符串
dp[0][i] = 0 空字符串s中有0个字符串t
dp[0][0] 空字符串s中有1个空字符串t
3)递推公式
若两个元素相等,那么就不考虑这个位置的元素 个数取决于:
1)前面已有的个数 dp[i-1][j-1] 2)字符串s中相邻两元素相同,模拟删除第一个(减1) dp[i-1][j]
if(s[i-1] == t[i-1]) dp[i][j] = dp[i-1][j-1] + dp[i-1][j]
若不等,则模拟将元素从字符串s删除掉(减1)
else dp[i][j] = dp[i-1][j]
4)遍历顺序
根据递推公式 从左向右遍历,从上到下遍历
for(int i = 1; i <= s.size(); i++){
for(int j = 1; j <= t.size(); j++){
}
}

5)打印dp数组

本题要求判断个数,所以要使用dp[s.size()][t.size()]求解最终的个数
如果再定义result与dp[i][j]比较了,会遇到这样的情况 s="eee" t="eee"会得到错误的结果3
因为这里面的每个e都相同,在中间过程会重复计数,所以会产生错误
所以还是应该使用dp[s.size()][t.size()]表示以s.size()-1结尾的字符串s中有t.size()-1结尾的字符串t的个数,说明字符串s遍历到了末尾的位置,求解的是全部的个数
代码
class Solution {
public:
int numDistinct(string s, string t) {
if(s.size() < t.size()) return 0;
//定义并初始化dp数组
vector<vector<uint64_t>> dp(s.size() + 1, vector<uint64_t>(t.size() + 1, 0));
//初始化dp数组
for(int i = 0; i <= s.size(); i++){
dp[i][0] = 1;
}
for(int i = 1; i <= s.size(); i++){
for(int j = 1; j <= t.size(); j++){
if(s[i-1] == t[j-1]){
dp[i][j] = dp[i-1][j-1] + dp[i-1][j];
}else {
dp[i][j] = dp[i-1][j];
}
// cout << "i=" << i << " " << "j=" << j << " " << dp[i][j] << endl;
}
}
return dp[s.size()][t.size()];
}
};- 时间复杂度: O(n * m)
- 空间复杂度: O(n * m)
题目3 583 两个字符串的删除操作
题目链接 583 两个字符串的删除操作
题意
返回使得单词word1和word2相同所需的最小步数,每步可以删除任意一个字符串中的一个字符。
动态规划
1)确定dp数组及下标i的含义
dp[i][j] 以word1[i-1]结尾的word1和以word2[j-1]结尾的word2相同的最小操作次数
2)dp数组初始化
根据递推公式 dp[0][j] = j dp[i][0] = i
其它下标对应的dp[i][j]可初始化为任意值
3)递推公式
两个字符相同时,操作次数不受影响取决于前面的情况
if(word[i-1] == word2[j-1]) dp[i][j] = dp[i-1][j-1];
两个字符不相同时,那么就要删除一个字符(操作次数+1) 或是 删除两个字符(操作次数+2)
else dp[i][j] = min(dp[i-1][j]+1,dp[i][j-1]+1,dp[i-1][j-1]+2)
4)遍历顺序
根据递推公式,从前向后遍历,从左向右遍历
for(int i = 1; i <= word1.size(); i++){
for(int j = 1; j < word2.size(); j++){
}
}

5)打印dp数组
代码
class Solution {
public:
int minDistance(string word1, string word2) {
//定义dp数组
vector<vector<int>> dp(word1.size() + 1, vector<int>(word2.size() + 2, 0));
for(int i = 0; i <= word1.size(); i++){
dp[i][0] = i;
}
for(int j = 0; j <= word2.size(); j++){
dp[0][j] = j;
}
for(int i = 1; i <= word1.size(); i++){
for(int j = 1; j <= word2.size(); j++){
if(word1[i-1] == word2[j-1]) dp[i][j] = dp[i-1][j-1];
else dp[i][j] = min(dp[i-1][j-1] + 2, min(dp[i-1][j] + 1, dp[i][j-1] + 1));
}
}
return dp[word1.size()][word2.size()];
}
};- 时间复杂度: O(n * m)
- 空间复杂度: O(n * m)
法2:使用最长公共子序列进行求解
word1.size() + word2.size() - 2 * coseqlen;
动态规划
1)确定dp数组及下标i的含义
dp[i][j] 以word1[i-1]结尾的word1和以word2[j-1]结尾的word2最长公共子序列的长度
2)dp数组初始化
根据递推公式 dp[0][j] = 0 dp[i][0] = 0
其它下标对应的dp[i][j]可初始化为任意值
3)递推公式
两个字符相同时,操作次数不受影响取决于前面的情况
if(word[i-1] == word2[j-1]) dp[i][j] = dp[i-1][j-1] + 1;
两个字符不相同时,那么就要删除一个字符(操作次数+1) 或是 删除两个字符(操作次数+2)
else dp[i][j] = max(dp[i-1][j],dp[i][j-1],dp[i-1][j-1])
4)遍历顺序
根据递推公式,从前向后遍历,从左向右遍历
for(int i = 1; i <= word1.size(); i++){
for(int j = 1; j < word2.size(); j++){
}
}
代码
class Solution {
public:
int minDistance(string word1, string word2) {
//定义dp数组
vector<vector<int>> dp(word1.size() + 1, vector<int>(word2.size() + 1, 0));
for(int i = 0; i <= word1.size(); i++){
dp[i][0] = 0;
}
for(int j = 0; j <= word2.size(); j++){
dp[0][j] = 0;
}
for(int i = 1; i <= word1.size(); i++){
for(int j = 1; j <= word2.size(); j++){
if(word1[i-1] == word2[j-1]){
dp[i][j] = dp[i-1][j-1] + 1;
}else{
dp[i][j] = max(dp[i-1][j-1], max(dp[i-1][j], dp[i][j-1]));
}
}
}
return word1.size() + word2.size() - 2 * dp[word1.size()][word2.size()];
}
};- 时间复杂度: O(n * m)
- 空间复杂度: O(n * m)
题目4 72 编辑距离
题目链接 72 编辑距离
题意
返回将word1转换为word2的最小次数(可以插入\删除\替换一个字符)
添加元素和删除元素是一个等价的操作(在word1中添加元素等价于在word2中删除元素)而替换操作是一个新的动作,需要另外考虑
动态规划
1)确定dp数组及下标i的含义
dp[i][j] 以word1[i-1]结尾的word1和以word2[j-1]结尾的word2相同的最小操作次数
2)dp数组初始化
根据递推公式 dp[i][0] = i dp[0][j] = j 其他下标对应的dp[i][j]可以初始化为任意值。
3)递推公式

if(word1[i-1] == word2[j-1]) dp[i][j] = dp[i-1][j-1];
else dp[i][j] = min(dp[i-1][j]+1,dp[i][j-1]+1,dp[i-1][j-1]+1);
注意本题多了一个操作就是替换的操作 而添加操作与删除操作是等价的
4)遍历顺序
根据递推公式 从上到下遍历,从左往右遍历
for(int i = 1; i <= word1.size(); i++){
for(int j = 1; j <= word2.size(); j++){
}
]
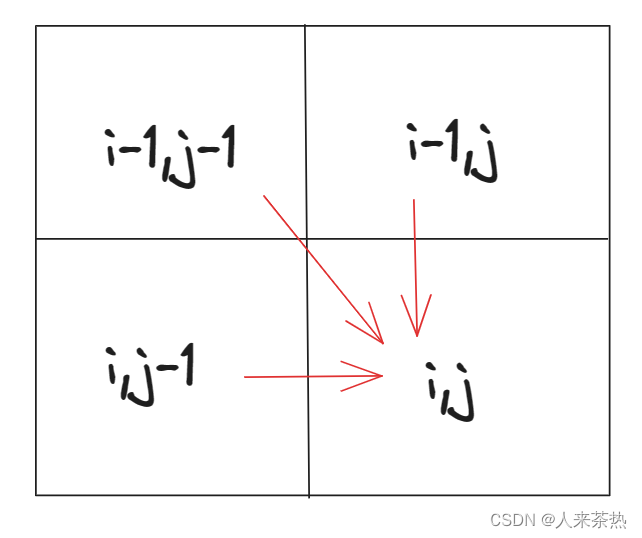
5)打印dp数组
代码
class Solution {
public:
int minDistance(string word1, string word2) {
//定义dp数组
vector<vector<int>> dp(word1.size() + 1, vector<int>(word2.size() + 1, 0));
//dp数组初始化
for(int i = 0; i <= word1.size(); i++){
dp[i][0] = i;
}
for(int j = 0; j <= word2.size(); j++){
dp[0][j] = j;
}
for(int i = 1; i <= word1.size(); i++){
for(int j = 1; j <= word2.size(); j++){
if(word1[i-1] == word2[j-1]) dp[i][j] = dp[i-1][j-1];
else dp[i][j] = min(dp[i-1][j-1] + 1, min(dp[i-1][j] + 1, dp[i][j-1] + 1));
}
}
return dp[word1.size()][word2.size()];
}
};- 时间复杂度: O(n * m)
- 空间复杂度: O(n * m)