系列文章:
LeetCode 热题 HOT 100(P1~P10)-CSDN博客
LeetCode 热题 HOT 100(P11~P20)-CSDN博客
LeetCode 热题 HOT 100(P21~P30)-CSDN博客
LeetCode 热题 HOT 100(P31~P40)-CSDN博客
LC76minimum_window
. - 力扣(LeetCode)
题目:
给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串,则返回空字符串 "" 。
输入:s = "ADOBECODEBANC", t = "ABC"
输出:"BANC"
解释:最小覆盖子串 "BANC" 包含来自字符串 t 的 'A'、'B' 和 'C'。
解法:
滑动窗口的思路,右游标可以探查到能满足条件的位置,关键的是左游标怎么确定合适的位置,因为左游标前面可能刚好是不在t中的字母。这个是第一个难点,这里通过维护一个缓存来表示字母的消耗情况,然后左游标就可以根据当前所在字母是否被过量使用判断。还有就是确定好了第一个滑动窗口left、right 之后怎么进入下一个滑动窗口的判断。这个时候left 游标要往前移动一位,同时字母消耗的缓存需要相应的处理,然后就可以继续往前滚动。
public String minWindow(String s, String t) {
// 这里根据题目给出的限定条件,只有英文字母,所以可以使用128位asc 来表示
int[] cache = new int[128];
int cnt = t.length();
for (int i = 0; i < t.length(); i++) {
cache[t.charAt(i)]++;
}
int begin = 0, min = 0;
for (int left = 0, right = 0; right < s.length(); right++) {
if (cache[s.charAt(right)] > 0) {
cnt--;
}
// 这里无差别-1,这样如果是负数就说明是t之外多余的
cache[s.charAt(right)]--;
if (cnt == 0) { //说明包含t
while (cache[s.charAt(left)] < 0) { // left指针尽可能往右走
cache[s.charAt(left)]++;
left++;
}
final int len = right - left + 1;
if (min == 0 || len < min) {
min = len;
begin = left;
}
//left 指针继续往前走,这个时候就破坏原来符合的情况了
cache[s.charAt(left)]++;
cnt++;
left++;
}
}
return s.substring(begin, begin + min);
}根据上面的思路结合代码就比较好理解了,这里缓存用int 数组表示,我发现很多时候数组比map 操作起来方便太多,这里先通过t 进行int 数组的初始化,然后在迭代过程中直接对下标-1,这样就能方便左游标是否可以往前移动。
这里还有个小技巧就是用cnt 来辅助判断是否满足条件,这样就不用轮询数组来判断。
LC78subsets
. - 力扣(LeetCode)
题目:
给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的
子集(幂集)。解集 不能包含重复的子集。你可以按 任意顺序 返回解集。
输入:nums = [1,2,3]
输出:[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
解法:
这类题目一闻就是递归的味道,基本套递归模板就可以了,这里要注意的是不要走回头路。
List<List<Integer>> result = new ArrayList<>();
public List<List<Integer>> subsets(int[] nums) {
dfs(nums, new ArrayList<>(), 0);
return result;
}
private void dfs(int[] nums, List<Integer> path, int level) {
result.add(new ArrayList<>(path));
for (int i = level; i < nums.length; i++) {
path.add(nums[i]);
dfs(nums, path, i + 1);
path.remove(path.size() - 1);
}
}在上面就是通过level 控制,注意在for 循环中下一次递归的时候不是level+1 而是i+1,需要注意体会里面的区别。
LC79word_search
. - 力扣(LeetCode)
题目:
给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。
单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
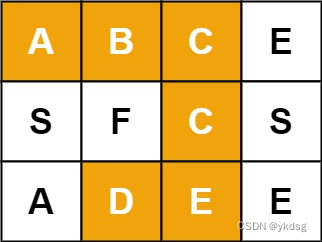
输入:board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出:true
解法:
基本也是递归的思路,首选肯定能通过循环判断word 第一个字母是否匹配,这样才有继续的基础,接下来就是往上下左右遍历可能的情况,这里的难点是怎么不走回头路,主要有2种思路:
- 使用一个额外的缓存来标识已经走过的路。
- 直接在原数组中用一个特殊字符覆盖已经走过的路径,这样肯定不会走回头路,因为字符肯定不匹配。
从代码整洁性来说第二种方式更优,这里的难点是递归完下一层之后要对之前造成的影响进行复原,这个不论选择哪种方式都一样。
public boolean exist(char[][] board, String word) {
final int m = board.length, n = board[0].length;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (dfs(board, i, j, word, 0)) {
return true;
}
}
}
return false;
}
private boolean dfs(char[][] board, int i, int j, String word, int index) {
if (index == word.length()) {
return true;
}
if (i < 0 || i == board.length || j < 0 || j == board[0].length || word.charAt(index) != board[i][j]) {
return false;
}
// 占掉一个位置,避免走回头路
board[i][j] = '#';
boolean result = dfs(board, i - 1, j, word, index + 1) || dfs(board, i, j - 1, word, index + 1) ||
dfs(board, i + 1, j, word, index + 1) || dfs(board, i, j + 1, word, index + 1);
board[i][j] = word.charAt(index);
return result;
}LC84largest_rectangle
. - 力扣(LeetCode)
题目:
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
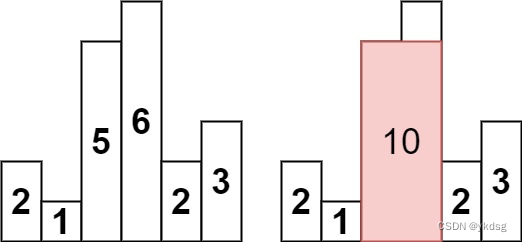
输入:heights = [2,1,5,6,2,3]
输出:10
解释:最大的矩形为图中红色区域,面积为 10
解法:
一般这类n根柱子、n个容器求最大面积的问题基本是用单调递增栈来解决。但是常规的单调递增栈需要解决刚开始栈中没元素的情况,以及最后栈中还遗留元素的情况。这样代码写起来就非常冗长,而且容易出错。
这里就涉及一个单调栈的优化技巧,通过左右哨兵的加入,就可以避免处理这些异常情况。
public int largestRectangleArea(int[] heights) {
//维护一个单调递增栈
Deque<Integer> stack = new ArrayDeque<>();
stack.push(-1); //放入左哨兵,能保证他始终在栈里面
int max = 0;
for (int i = 0; i <= heights.length; i++) { // 这里使用heights.length 作为右哨兵
while (getH(heights, i) < getH(heights, stack.peek())) {
final Integer pre = stack.pop();
int area = (i - stack.peek() - 1) * getH(heights, pre);
max = Math.max(max, area);
}
stack.push(i);
}
return max;
}
private int getH(int[] heights, int index) {
if (index == -1 || index == heights.length) {
return -1;
}
return heights[index];
}这里通过左哨兵-1,保证了栈中肯定有值,而且下标0 的元素加入的时候天然满足递增条件。然后右哨兵-1 能保证把栈中所有元素都倒逼出来,这样就不用处理栈中还留有元素的情况。
LC94binary_tree
. - 力扣(LeetCode)
题目:
给定一个二叉树的根节点 root ,返回 它的 中序 遍历 。
解法:
如果用递归的方法是很简单的,思路也很清晰。通过代码能直观感受
public List<Integer> inorderTraversalRecur(TreeNode root) {
List<Integer> result = new ArrayList<>();
if (root == null) {
return result;
}
result.addAll(inorderTraversalRecur(root.left));
result.add(root.val);
result.addAll(inorderTraversalRecur(root.right));
return result;
}如果不能使用递归,或者想要挑战下自己,那这道题的难度就上升了一个等级。核心是遍历的时候必然会用到栈,但是怎么判断当前节点是之前已经迭代过可以直接输出,还是需要迭代子节点。这里有2种解法:
第一种:颜色标记法,就是在node 中增加颜色属性,用于标识当前是否可以直接输出
public List<Integer> inorderTraversalColor(TreeNode root) {
List<Integer> result = new ArrayList<>();
if (root == null) {
return result;
}
Deque<ColorNode> stack = new ArrayDeque<>();
stack.push(new ColorNode(0, root));
while (!stack.isEmpty()) {
final ColorNode cnode = stack.pop();
TreeNode node = cnode.node;
if (node == null) {
continue;
}
if (cnode.color == 0) {
//需要注意这里的顺序,因为是栈所以要先放最后轮询的节点
stack.push(new ColorNode(0, node.right));
stack.push(new ColorNode(1, node));
stack.push(new ColorNode(0, node.left));
} else {
result.add(node.val);
}
}
return result;
}
static class ColorNode {
/**
* 表示是否应该输出,0,表示未遍历子树,1表示输出当前值
*/
int color;
TreeNode node;
public ColorNode(int color, TreeNode node) {
this.color = color;
this.node = node;
}
}可以发现,通过增加一个颜色字段之后这里用0、1 表示是否需要迭代子节点,整体代码逻辑就很顺,比较符合我们的逻辑。
还有一种是纯用栈的方式,这样就需要维护一个cur 指针,同时判断cur 和栈的情况,在cur 不为空的时候不断往左树迭代同时入栈,如果cur 为空就出栈,并把cur 指向右节点。
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> result = new ArrayList<>();
Deque<TreeNode> stack = new ArrayDeque<>();
TreeNode cur = root;
while (cur != null || !stack.isEmpty()) {
if (cur != null) {
//不断往左子树迭代,并将当前节点保存到栈中
stack.push(cur);
cur = cur.left;
} else { //左子树走到底,进行出栈并记录
final TreeNode node = stack.pop();
result.add(node.val);
// 如果有右节点继续上面的过程
cur = node.right;
}
}
return result;
}代码虽然比上一种简洁,但是理解难度高了不少,如果吃透这种写法,基本也能玩得转二叉树类型的题目了。
LC96unique_binary
. - 力扣(LeetCode)
题目:
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
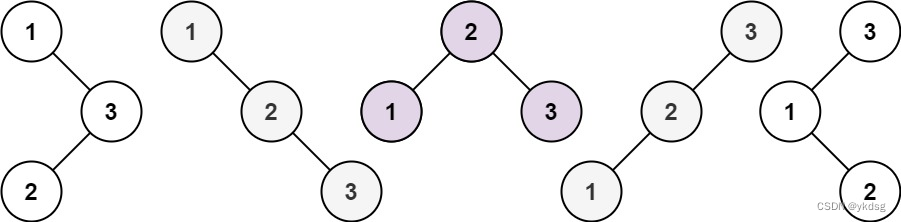
输入:n = 3
输出:5
解法:
看着像二叉树类型的题目,实际是动态规划的思路,核心就是动态数组的定义和动态方程的推导:
i 表示以第i个节点(从1开始)为根节点的子树,左子树个数为i,右子树个数为n-i-1
f(i) 表示i为根节点时组合个数,G(i) 表示i个节点存在的组合
G(n)=f(1)+f(2)+...+f(n)
f(i)=G(i−1)∗G(n−i)
G(n) = G(0)*G(n-1) + G(1)*G(n-2)+...+G(n-1)*G(0)
dp[n] 表示n 个节点的组合数
尝试自己推导一遍,还是能理解的,代码写出来其实很简单
public int numTrees(int n) {
if (n < 2) {
return 1;
}
int[] dp = new int[n + 1];
dp[0] = 1;
dp[1] = 1;
for (int i = 2; i <= n; i++) {
//以第j个为 根节点时对应的组合数
for (int j = 1; j <= i; j++) {
dp[i] += dp[j - 1] * dp[i - j];
}
}
return dp[n];
}但是不理解上面的推导过程,确实是看不懂。
LC98validate_binary
. - 力扣(LeetCode)
题目:
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
- 节点的左
子树
只包含 小于 当前节点的数。 - 节点的右子树只包含 大于 当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
解法:
刚一开始,就想到了用递归的方法来解决这个问题,先判断当前节点是否合法(左值<当前值<右值),递归判断左节点,最后递归右节点。结果啪啪打脸,这里存在一个问题是这样的判断不严谨,可能左子树其中一个叶子节点满足直属父节点和兄弟节点的关系,但是并不满足跟祖父节点的约束。
因此这里需要基于中序遍历是递增关系这条更严格的约束条件。
Integer preVal;
public boolean isValidBST(TreeNode root) {
if (root == null) {
return true;
}
if (!isValidBST(root.left)) {
return false;
}
if (preVal != null && root.val <= preVal) {
return false;
}
preVal = root.val;
return isValidBST(root.right);
}注意这里使用了包装类型Integer,方便处理第一次赋值的特殊情况。
LC101symmetric_tree
. - 力扣(LeetCode)
题目:
给你一个二叉树的根节点 root , 检查它是否轴对称。
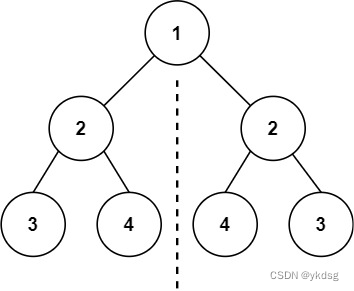
解法:
这类一想就有很多子情况需要判断的题目,基本要么递归要么动态规划。或者说他俩基本是一回事。
实际就是判断左节点跟右节点是否对称
public boolean isSymmetric(TreeNode root) {
if (root == null) {
return true;
}
return dfs(root.left, root.right);
}
private boolean dfs(TreeNode left, TreeNode right) {
if (left == null && right == null) {
return true;
}
// 到这里说明left和right 不会同时为null,那么其中有一个null 就说明不对称
if (left == null || right == null) {
return false;
}
if (left.val != right.val) {
return false;
}
return dfs(left.left, right.right) && dfs(left.right, right.left);
}可以看到复杂的地方是对边界情况的处理,是否都为null啊,或者其中一个为null,当都不为null 的时候判断是否相等。然后最后再递归,注意这里left.left 对应right.right,这个看下轴对称示意图就很好理解了。
LC102binary_tree
. - 力扣(LeetCode)
题目:
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
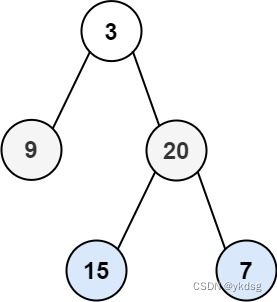
输入:root = [3,9,20,null,null,15,7] 输出:[[3],[9,20],[15,7]]
解法:
首先想到的是通过队列进行广度遍历,但是第二个问题是怎么知道当前是那一层,因为需要按层输出。这里有个小技巧就是在遍历队列的时候,直接判断当前队列的长度,这个就是当前层的节点数。
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> result = new ArrayList<>();
if (root == null) {
return result;
}
Queue<TreeNode> queue = new ArrayDeque<>();
queue.add(root);
while (!queue.isEmpty()) {
final int size = queue.size();
List<Integer> levelResult = new ArrayList<>();
for (int i = 0; i < size; i++) {
final TreeNode node = queue.poll();
levelResult.add(node.val);
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
}
result.add(levelResult);
}
return result;
}行数虽多,但是很多是对边界情况的处理,整体还是很好理解的。
LC104maximum_depth
. - 力扣(LeetCode)
题目:
给定一个二叉树 root ,返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
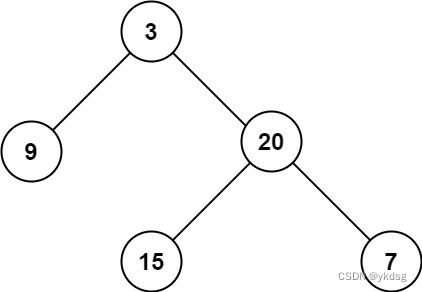
输入:root = [3,9,20,null,null,15,7] 输出:3
题解:
这个也是递归的思路,从左子树、右子树中选择最深的节点数+1 就是当前的最大深度。
public int maxDepth(TreeNode root) {
if (root == null) {
return 0;
}
return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;
}代码非常简单,只能说递归真是非常强大。