Leetcode.45题:跳跃游戏II
/*
题意的理解:
nums[0] 只能跳 1 ~ nums[0]步
依次类推:从nums[0] - nums[n - 1] 最少需要多少步数
nums = 2 3 1 1 4
nums[0] = 2,初始只能跳 1/2步,如跳1步,达到nums[1]
而nums[1] = 3,顾第二部可以跳的长度为 1 ~ 3
如果我们跳3步,恰巧走到结尾,最少跳跃步数为2
此题较难:贪心
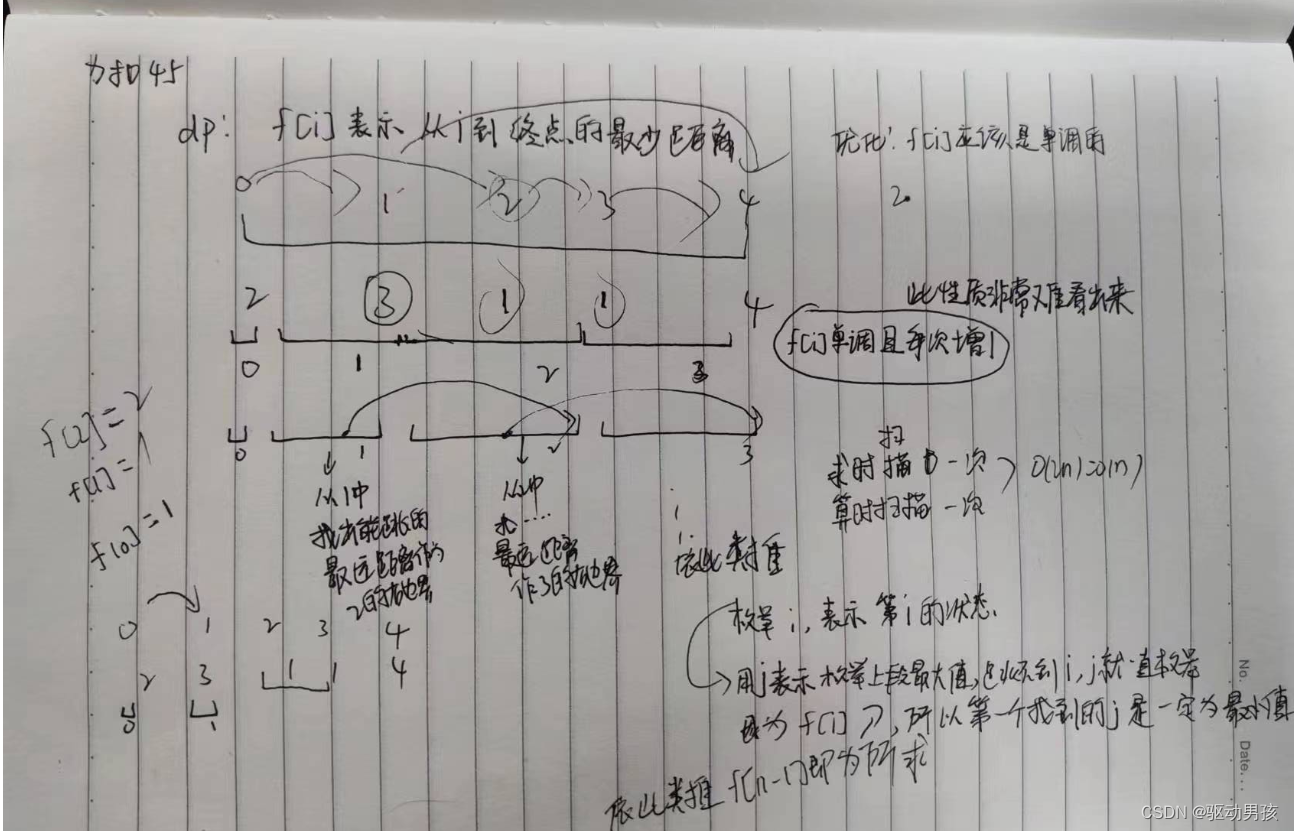
dp: f[i]表示从起点道i的最小距离
优化f[i]应该是单调的,从0开始,每次 + 1
单调区间从0 1 2 3 4 5... 分别为到达i出的最小举例用f[i]维护
j表示上段,能跳到i处的距离,因为从左往右找的j,第一次找的j一定是最小值
j一定是i的上一段,比如 i = 3,j 应该在0 1 2,如果在j = 0 1 2 段的任意nums[j] + j不够在i内了,j就++,到下一段
*/
class Solution {
public:
int jump(vector<int>& nums) {
int n = nums.size();
vector<int> f(n);
for(int i = 1, j = 0; i < n; i++){ // i是从第1段开始枚举,而j是从第0段开始枚举的
// j在该段 + nums[j] 不能够在i段内或者大于等于i出,j就该往下一段了
while(j + nums[j] < i) j++;
f[i] = f[j] + 1; // 单调递增,每次增加 + 1
}
return f[n - 1];
}
};