文章目录
- 1. 二叉树特点
- 1.1 完全二叉树
- 1.2 满二叉树
- 2. 二叉树创建
- 2.1 通过先序序列带有叶子结点标识符创建二叉树
- 2.2 通过层次遍历顺序创建二叉树
- 2.3 通过 先序+中序 创建二叉树
- 2.4 通过 先序+中序 创建二叉树
- 2.5 通过 中序+后序 创建二叉树
- 3. 二叉树遍历通用方法
- 3.1 先序遍历(深度递归)
- 3.2 中序遍历(深度递归)
- 3.3 后序遍历(深度递归)
- 3.4 广度优先遍历(BFS)
- 4. 常见面试题
- 4.1 二叉树的中序遍历
- 4.2 二叉树的最大深度
- 4.3 翻转二叉树
- 4.4 对称二叉树
- 4.5 二叉树的直径
- 4.6 二叉树的层序遍历
- 4.7 将有序数组转换为二叉搜索树
- 5. 参考文档
二叉树常见的使用方法逻辑整理
1. 二叉树特点
二叉树是每个节点最多有两个子树的树结构。通常子树被称作“左子树”(left subtree)和“右子树”(right subtree)。
二叉树特点
- 性质1: 在二叉树的第i层上至多有2^(i-1)个结点(i>0)
- 性质2: 深度为k的二叉树至多有2^k - 1个结点(k>0)
- 性质3: 对于任意一棵二叉树,如果其叶结点数为N0,而度数为2的结点总数为N2,则N0=N2+1;
- 性质4:具有n个结点的完全二叉树的深度必为 log2(n+1)
- 性质5:对完全二叉树,若从上至下、从左至右编号,则编号为i 的结点,其左孩子编号必为2i,其右孩子编号必为2i+1;其双亲的编号必为i/2(i=1 时为根,除外)
1.1 完全二叉树
完全二叉树——若设二叉树的高度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第h层有叶子结点,并且叶子结点都是从左到右依次排布,这就是完全二叉树。
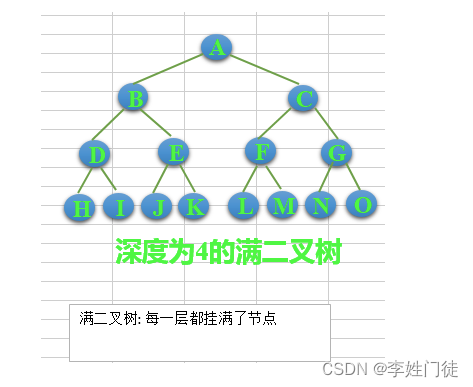
1.2 满二叉树
除了叶结点外每一个结点都有左右子叶且叶子结点都处在最底层的二叉树。
2. 二叉树创建
class Node():
def __init__(self, val):
self.val = val
self.left = None
self.right = None
class Tree():
def __init__(self):
self.root = None
self.queue = [] #用来存放正在操作的三个树节点,分别是root,left和right
self.create_queue = [] #用来存放先序序列来创建二叉树
2.1 通过先序序列带有叶子结点标识符创建二叉树
#通过先序序列创建二叉树,没有左右子节点被标记为'#'
def createTree(self):
current = self.create_queue.pop(0)
if current != '#':
new_node = Node(current)
if self.root is None:
self.root = new_node
new_node.left = self.createTree()
new_node.right = self.createTree()
return new_node
return None
2.2 通过层次遍历顺序创建二叉树
#通过层次遍历顺序创建二叉树
def add(self, val):
new_node = Node(val)
self.queue.append(new_node)
if self.root is None:
self.root = new_node
return
tree_node = self.queue[0]
if tree_node.left is None:
tree_node.left = new_node
else:
tree_node.right = new_node
self.queue.pop(0)
2.3 通过 先序+中序 创建二叉树
#通过前序序列和中序序列创建二叉树
def create_tree(self, pre_order, mid_order):
if len(pre_order) == 0:
return None
new_node = Node(pre_order[0])
if self.root is None:
self.root = new_node
i = mid_order.index(pre_order[0])
print(i)
new_node.left = self.create_tree(pre_order[1:1+i], mid_order[:i])
new_node.right = self.create_tree(pre_order[1+i:], mid_order[i+1:])
return new_node
2.4 通过 先序+中序 创建二叉树
#通过前序序列和中序序列创建二叉树
def create_tree(self, pre_order, mid_order):
if len(pre_order) == 0:
return None
new_node = Node(pre_order[0])
if self.root is None:
self.root = new_node
i = mid_order.index(pre_order[0])
print(i)
new_node.left = self.create_tree(pre_order[1:1+i], mid_order[:i])
new_node.right = self.create_tree(pre_order[1+i:], mid_order[i+1:])
return new_node
2.5 通过 中序+后序 创建二叉树
#通过中序和后序创建二叉树
def construct_tree(self, mid_order, post_order):
length = len(post_order)
if length == 0:
return None
new_node = Node(post_order[-1])
if self.root is None:
self.root = new_node
i = mid_order.index(post_order[-1])
new_node.left = self.construct_tree(mid_order[:i], post_order[:i])
new_node.right = self.construct_tree(mid_order[i+1:], post_order[length-2-i:length-1])
return new_node
3. 二叉树遍历通用方法
二叉树的遍历方式通常有2种
- 深度搜索(dfs):先序遍历、中序遍历、后序遍历
- 广度搜索(bfs): 广度优先遍历
针对深度搜索的3种方式,对应的访问路径不同,需要根据实际情况进行调整
3.1 先序遍历(深度递归)
#通过递归进行先序遍历
def dfs(self, root):
if root is None: return
print(root.val)
self.recursion_vlr(root.left)
self.recursion_vlr(root.right)
遍历顺序:根节点→左孩子→右孩子,注意所有子树都是按照该顺序访问
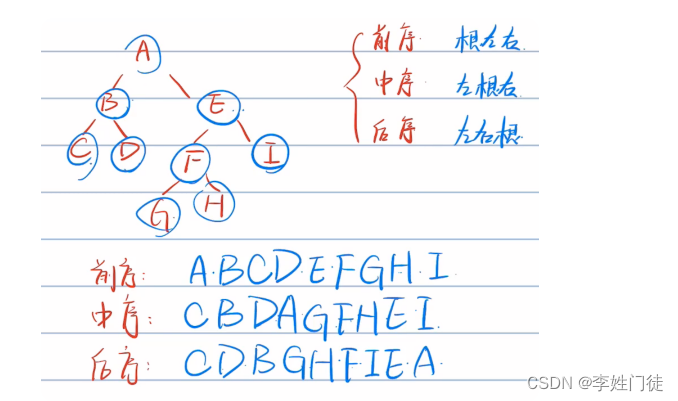
3.2 中序遍历(深度递归)
#通过递归进行中序遍历
def dfs(self, root):
if root is None: return
self.recursion_lvr(root.left)
print(root.val)
self.recursion_lvr(root.right)
遍历顺序:左孩子→根节点→右孩子,注意所有子树都是按照该顺序访问
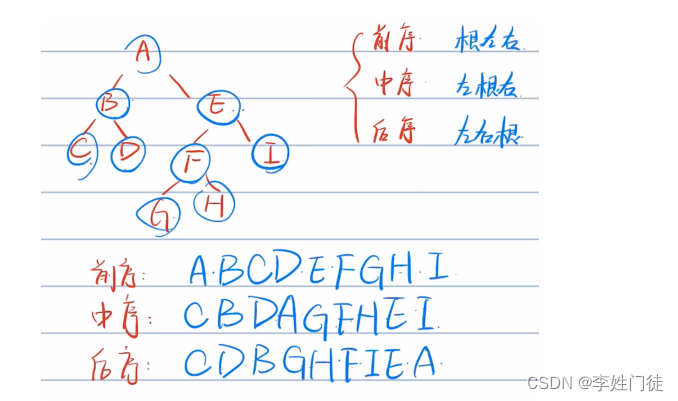
3.3 后序遍历(深度递归)
#通过递归进行后序遍历
def dfs(self, root):
if root is None: return
self.recursion_lrv(root.left)
self.recursion_lrv(root.right)
print(root.val)
遍历顺序:左孩子→根节点→右孩子,注意所有子树都是按照该顺序访问
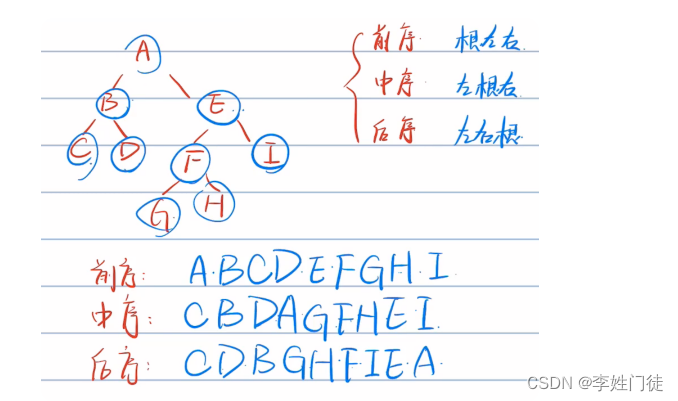
3.4 广度优先遍历(BFS)
#利用队列进行广度优先遍历BFS
def bfs(self):
queue = []
current = self.root
queue.append(current)
while queue:
current = queue.pop(0)
print(current.val)
if current.left: queue.append(current.left)
if current.right: queue.append(current.right)
4. 常见面试题
一些总结
4.1 二叉树的中序遍历
给定一个二叉树的根节点 root ,返回 它的 中序 遍历 。
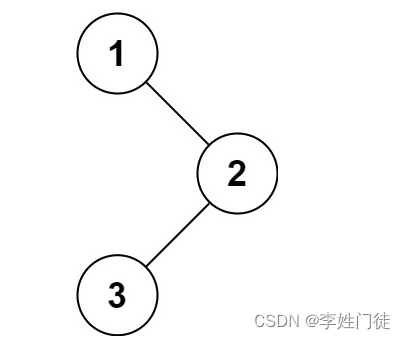
输入:root = [1,null,2,3]
输出:[1,3,2]
示例 2:
输入:root = []
输出:[]
示例 3:
输入:root = [1]
输出:[1]
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution(object):
def inorderTraversal(self, root):
"""
:type root: TreeNode
:rtype: List[int]
"""
rs = []
def dfs(root, res):
if root is None:
return
dfs(root.left,res)
res.append(root.val)
dfs(root.right,res)
dfs(root, res)
return res
4.2 二叉树的最大深度
给定一个二叉树 root ,返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
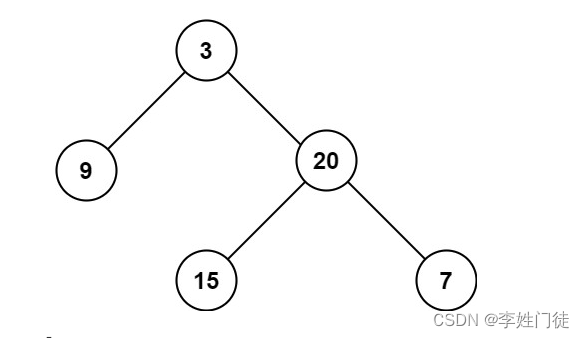
输入:root = [3,9,20,null,null,15,7]
输出:3
示例 2:
输入:root = [1,null,2]
输出:2
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution(object):
def maxDepth(self, root):
"""
:type root: TreeNode
:rtype: int
"""
if root is None: return 0
left_height = self.maxDepth(root.left)
right_height = self.maxDepth(root.right)
return max(left_height, right_height) + 1
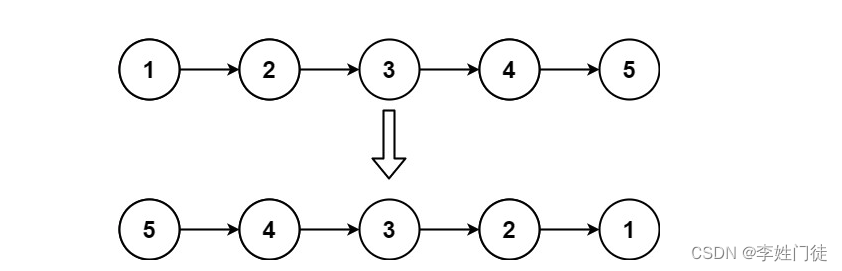
4.3 翻转二叉树
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
示例 1:
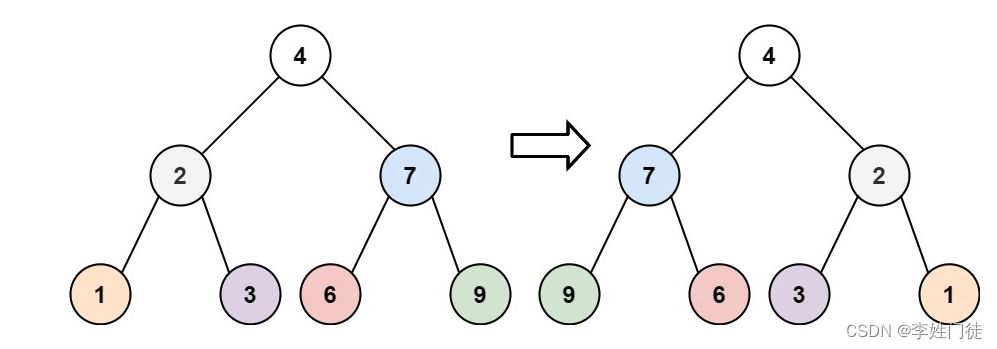
输入:root = [4,2,7,1,3,6,9]
输出:[4,7,2,9,6,3,1]
示例 2:
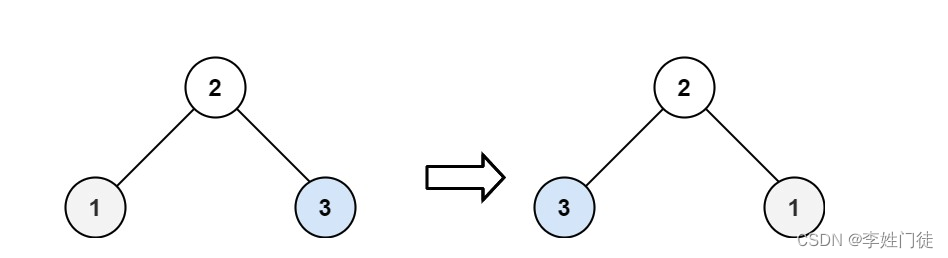
输入:root = [2,1,3]
输出:[2,3,1]
示例 3:
输入:root = []
输出:[]
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution(object):
def invertTree(self, root):
"""
:type root: TreeNode
:rtype: TreeNode
"""
if not root:return None
root.left, root.right = root.right, root.left
self.invertTree(root.left)
self.invertTree(root.right)
return root
4.4 对称二叉树
给你一个二叉树的根节点 root , 检查它是否轴对称。
示例 1:
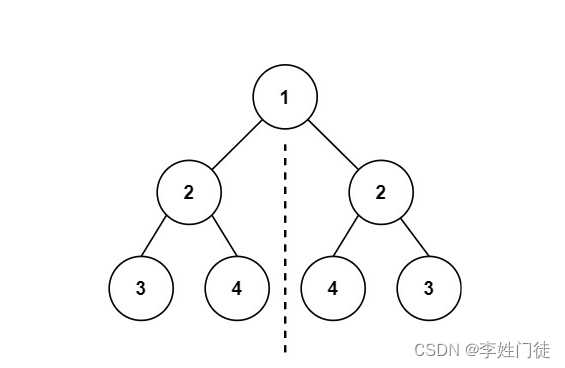
输入:root = [1,2,2,3,4,4,3]
输出:true
示例 2:
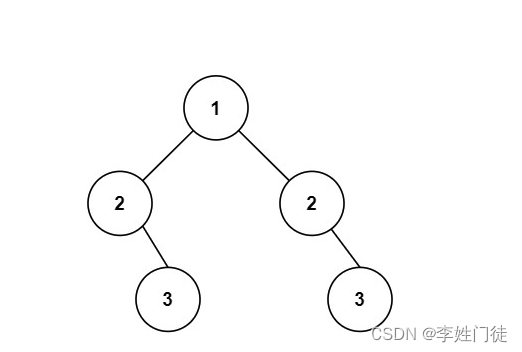
输入:root = [1,2,2,null,3,null,3]
输出:false
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution(object):
def isSymmetric(self, root):
"""
:type root: TreeNode
:rtype: bool
"""
if not root:return True
def dfs(left, right):
if not (left or right): return True
if not (left and right): return False
if left.val != right.val: return False
return dfs(left.right, right.left) and dfs(left.left, right.right)
return dfs(root.left, root.right)
4.5 二叉树的直径
给你一棵二叉树的根节点,返回该树的 直径 。
二叉树的 直径 是指树中任意两个节点之间最长路径的 长度 。这条路径可能经过也可能不经过根节点 root 。
两节点之间路径的 长度 由它们之间边数表示。
示例 1:
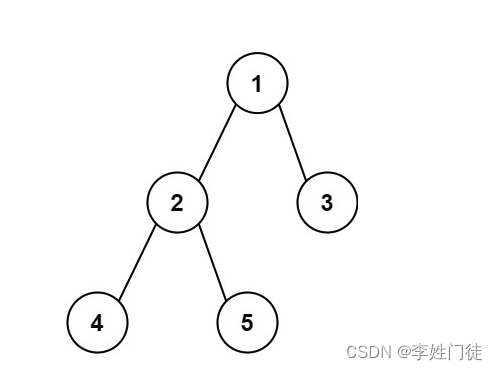
输入:root = [1,2,3,4,5]
输出:3
解释:3 ,取路径 [4,2,1,3] 或 [5,2,1,3] 的长度。
示例 2:
输入:root = [1,2]
输出:1
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution(object):
def diameterOfBinaryTree(self, root):
"""
:type root: TreeNode
:rtype: int
"""
self.res = 1
def dfs(root):
if root is None: return 0
l = dfs(root.left)
r = dfs(root.right)
self.res = max(self.res, l + r + 1)
return max(l,r) + 1
dfs(root)
return self.res -1
4.6 二叉树的层序遍历
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
示例 1:
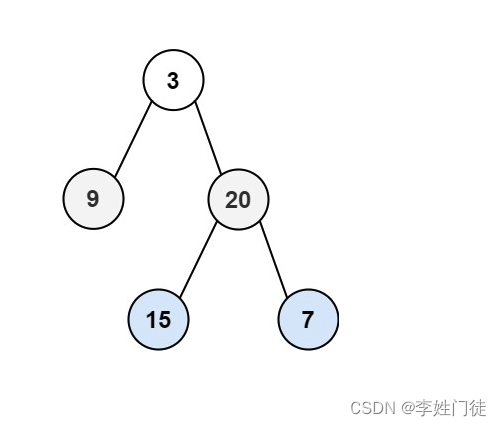
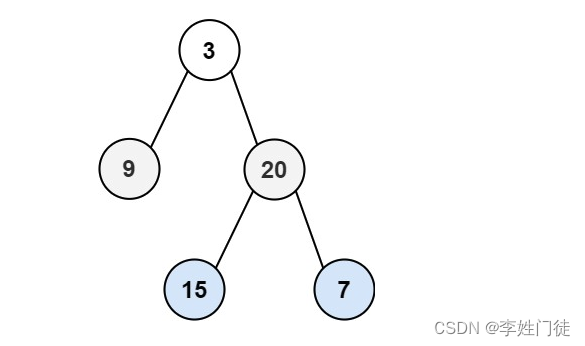
输入:root = [3,9,20,null,null,15,7]
输出:[[3],[9,20],[15,7]]
示例 2:
输入:root = [1]
输出:[[1]]
示例 3:
输入:root = []
输出:[]
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution(object):
def levelOrder(self, root):
"""
:type root: TreeNode
:rtype: List[List[int]]
"""
res = []
if not root: return res
queue = [root]
while queue:
size = len(queue)
tmp = []
for _ in range(0, size):
r = queue.pop(0)
tmp.append(r.val)
if r.left: queue.append(r.left)
if r.right: queue.append(r.right)
res.append(tmp)
return res
4.7 将有序数组转换为二叉搜索树
给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵平衡二叉搜索树。
示例 1:
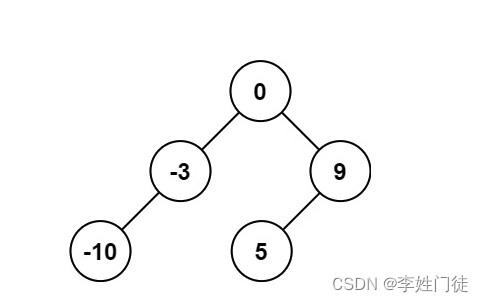
输入:nums = [-10,-3,0,5,9]
输出:[0,-3,9,-10,null,5]
解释:[0,-10,5,null,-3,null,9] 也将被视为正确答案:
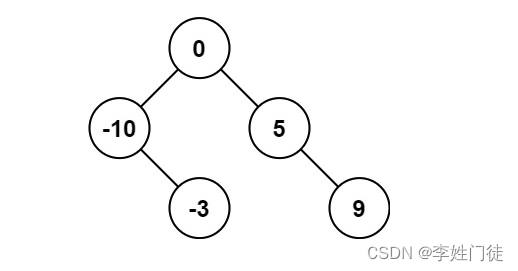
示例 2:
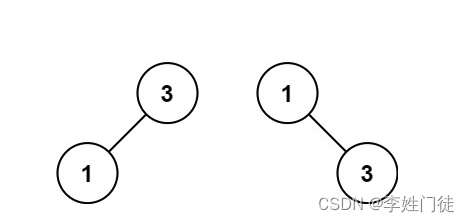
输入:nums = [1,3]
输出:[3,1]
解释:[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution(object):
def sortedArrayToBST(self, nums):
"""
:type nums: List[int]
:rtype: TreeNode
"""
def dfs(nums, low, high):
if(low > high): return
# 以中间树作为根
mid = low + (high - low) /2
root = TreeNode(nums[mid])
root.left = dfs(nums, low, mid - 1)
root.right = dfs(nums, mid + 1, high)
return root
return dfs(nums, 0, len(nums) - 1)
5. 参考文档
暂无,相关面试题请参考letcode以及相关说明