给定一个仅包含字符的字符串(’ 和 ‘)’，返回最长有效的长度(出色地-形成) 括号子弦。

示例1：

输入：s = “(()”
输出：2
说明：最长的有效括号子字符串是 “()” 。

示例2：

输入：s = “)()())”
输出：4
说明：最长的有效括号子字符串是 “()()” 。

示例3：

输入：s = “”
输出：0

约束：

0 <= s.length <= 3* 104
s[i] 是 ‘(’， 或者 ‘)’。

解决方案 ：

方法
在这里，方法无非是我们使用堆栈，当我们遇到开头支撑时，我们将其索引推入堆栈中，每当我们触摸闭合支架时，我们就会看到堆栈的顶部，如果它的大小是一个，则意味着闭合括号已经统治了开头括号。然后，我们将堆栈的最高值编辑为闭合支架的索引。
如下所示，图片清楚地描绘了此方法。

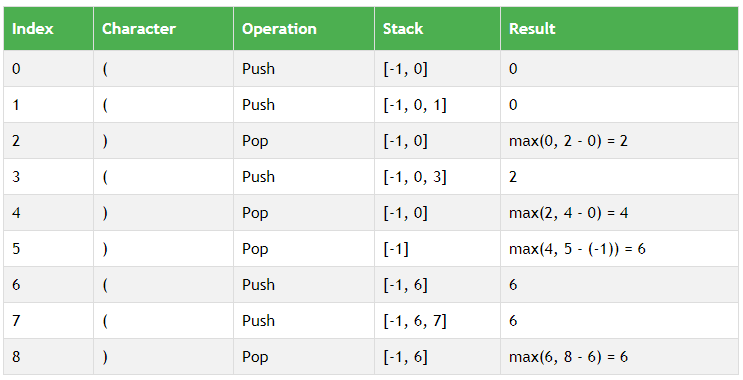
• 在这里给出作为行Ans = max给出的答案(ans，索引- stk.top()) 只有当堆栈的大小不是1时，就会遇到闭合支架。

代码

class Solution {
public:
    int longestValidParentheses(string s) {
        stack<int>stk;
        stk.push(-1);
        int ans = 0;
        for(int i = 0 ; i < s.size();  i++)
        {
            if(s[i] == '(')
                stk.push(i);
            else
            {
                if(stk.size() == 1)
                    stk.top() = i;
                else
                {
                    stk.pop();
                    ans = max(ans , i - stk.top());
                }
            }
        }
        return ans;
    }
};

class Solution {
    public int longestValidParentheses(String s) {
    int leftCount = 0;
    int rightCount = 0;
    int maxLength = 0;

    for (int i = 0; i < s.length(); i++) {
        if (s.charAt(i) == '(') {
            leftCount++;
        } else {
            rightCount++;
        }

        if (leftCount == rightCount) {
            maxLength = Math.max(maxLength, 2 * rightCount);
        } else if (rightCount > leftCount) {
            leftCount = rightCount = 0;
        }
    }

    leftCount = rightCount = 0;

    for (int i = s.length() - 1; i >= 0; i--) {
        if (s.charAt(i) == '(') {
            leftCount++;
        } else {
            rightCount++;
        }

        if (leftCount == rightCount) {
            maxLength = Math.max(maxLength, 2 * leftCount);
        } else if (leftCount > rightCount) {
            leftCount = rightCount = 0;
        }
    }

    return maxLength;
    }
}

class Solution:
    def longestValidParentheses(self, s: str) -> int:
        stack=[]
        l=['0']*len(s)
        for ind,i in enumerate(s):
            if i=='(':
                stack.append(ind)
            else:
                if stack:
                    l[stack.pop()]='1'
                    l[ind]='1'
        return max(len(i) for i in ''.join(l).split('0'))

复杂

• 时间复杂性：这里的复杂性是$$o(n)$$，因为我们仅使用一个只有一个带有堆栈的循环，因此它以线性复杂性运行。
• 空间复杂性：这里的空间复杂性将为$ o(n)$，因为我们只使用了一个堆栈，它也将元素也存储在最坏的情况下，因此可以使人变得复杂。