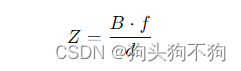【matlab下的双目内窥镜标定与深度测距-双目成像原理】

介绍

双目成像是一种利用两个摄像头或摄像头组成的系统同时捕捉场景信息的技术。它模拟了人类双眼视觉系统，通过两个视角获取的图像来计算深度信息，从而实现三维感知和场景重建。

坐标系关系

在双目成像方法中共存在四个坐标系：

世界坐标系：是一个三维空间中的坐标系，用来描述物体在真实世界中的位置和姿态。在计算机视觉和机器人领域中，世界坐标系通常被定义为一个固定的参考系，例如地面上的坐标系或者某个物体表面的坐标系。

相机坐标系：是以相机为中心的坐标系，用来描述物体相对于相机的位置和姿态。相机坐标系是一个相对坐标系，其原点通常位于相机的光学中心，坐标轴与相机的视觉轴（光轴）对齐。相机坐标系提供了连接世界坐标系和图像坐标系之间的桥梁。

图像坐标系：描述真实物体在相机焦距处成像的坐标系。图像坐标系的原点通常位于图像的左上角，x轴向右延伸，y轴向下延伸。图像坐标系中的点表示物体在图像上的投影位置，是实际成像过程中的数字表示。

像素坐标系：是图像坐标系的数字化版本，用来描述物体在照片上数字图像的位置。像素坐标系中的点是由图像中的像素点组成，每个像素点都有唯一的坐标位置，通常以整数表示。像素坐标系的单位是像素，是数字图像处理和计算机视觉中常用的坐标系统。

双目成像的目的即是，将建立像素坐标系中某一点到世界坐标系中的关系，通过像素坐标系的一点，得到与其对应世界坐标系相对于相机的深度距离。，显然像素坐标系是二维，世界坐标系是三维，需要向更高维度进行映射。

相互关系推导

世界坐标系到相机坐标系的转换：
旋转矩阵
R：描述世界坐标系到相机坐标系的旋转关系。
平移向量
t：描述世界坐标系到相机坐标系的平移关系

相机坐标系到图像坐标系的转换：
内参矩阵
K：包括焦距、主点坐标和畸变参数，描述相机坐标系到图像坐标系的投影关系。
坐标归一化矩阵
N：将相机坐标系中的三维坐标转换为图像坐标系中的二维坐标。

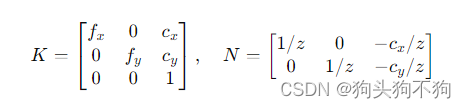
其中，f x​ 和 f y​ 是相机的水平和垂直焦距，c x​ 和 c y​ 是主点的水平和垂直坐标，z 是相机坐标系中的深度。

图像坐标系到像素坐标系的转换：
分辨率矩阵 M：描述图像坐标系中的单位长度与像素坐标系中的单位长度之间的关系。

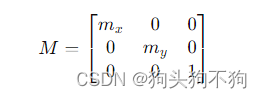
其中，m x​ 和 m y​ 是图像的水平和垂直分辨率

相机中感光器件的每个像素物理尺寸为dx*dy，则图像坐标系中的坐标（x，y）与像素坐标系中的坐标（u，v）之间的关系可以表示为：

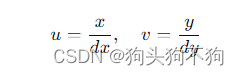
这个关系可以用矩阵形式表示为：

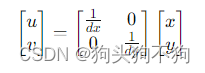
则像素坐标系到世界坐标系的映射关系：

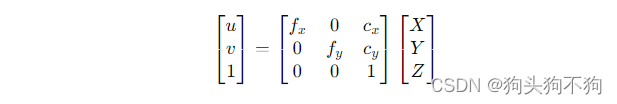
如果加上在世界坐标系中的旋转矩阵R和平移向量T有：

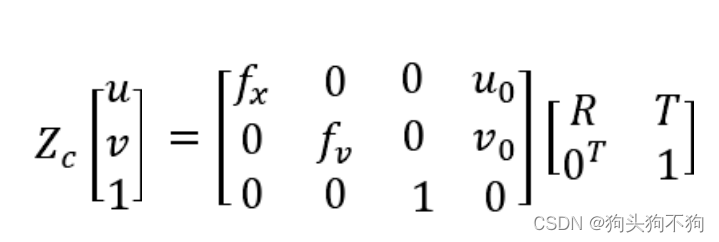
完成转换

三角测量

利用已知的基线长度（两个摄像头之间的距离）和视差角度，可以使用三角测量法计算物体的距离

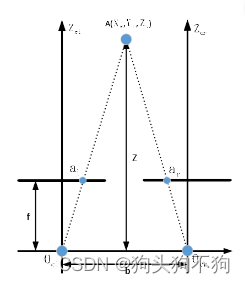
视差（Disparity）：视差表示在两个摄像头之间看到同一物体时，该物体在图像中的位置差异。视差d与物体距离Z之间有以下关系：

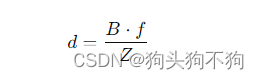
其中，B是基线长度（两个摄像头之间的距离），f是焦距。

通过视差d和基线长度B可以计算出物体的深度Z：