【Hello算法】＞第 2 关＞数据结构之数组与链表

数据结构之数组与链表

- 1：Understanding data structures ！
- ——了解数据结构——
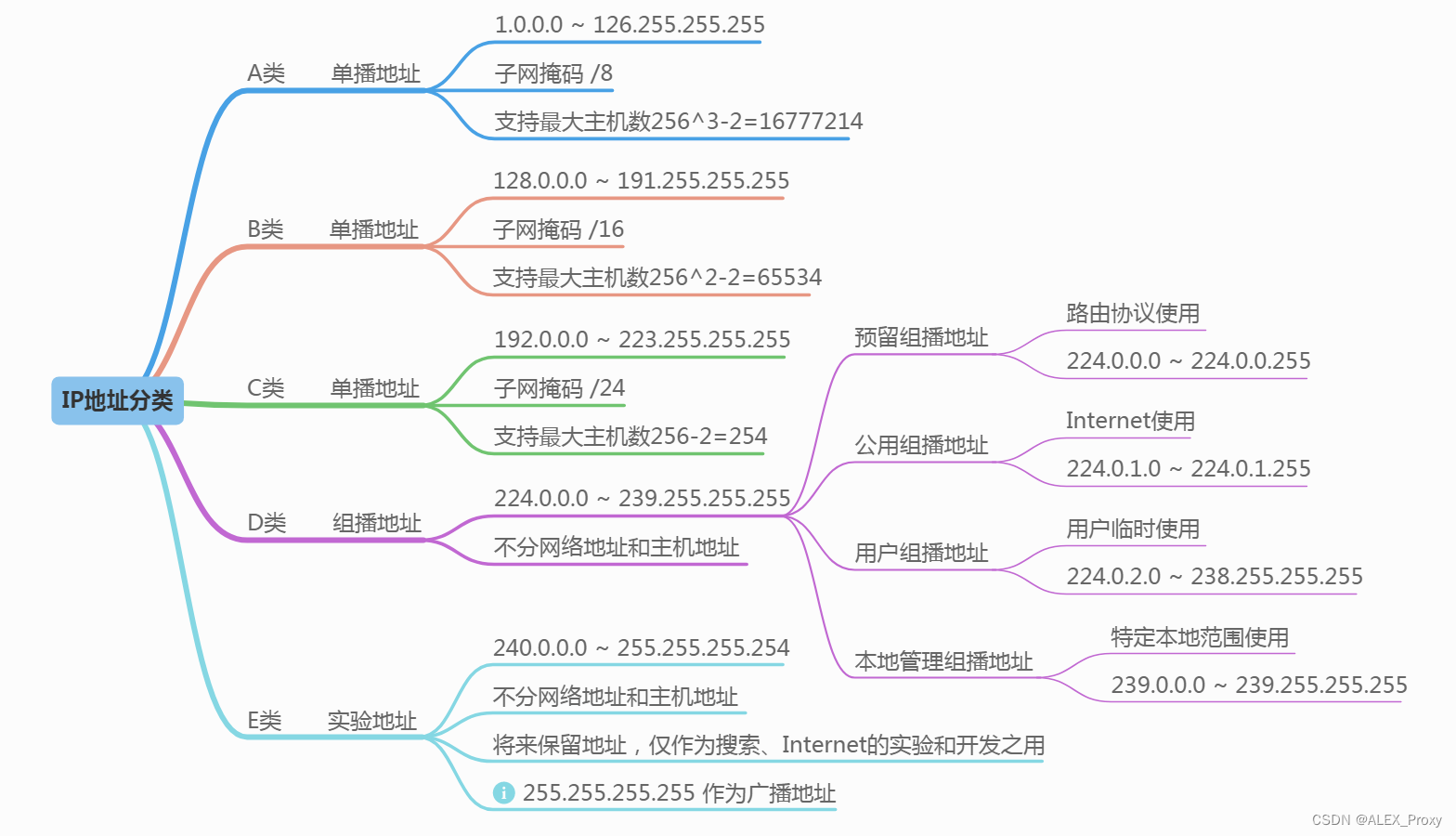
- - 1.1：Classification-分类-
  - 1.2：Type-类型-
- 2：Arrays are the bricks that make up the wall of data structures *
- ——数组是组成数据结构这堵墙的一块块砖——
- - 2.1：Common operations-常用操作-
  - 2.2：A&D-优缺点-
  - 2.3：Applicationg-应用-
- 3：A linked list is a vine that shuttles between these bricks *
- ——链表是穿梭在这些砖块间的藤蔓——
- - 3.1：Common operations-常用操作-
  - 3.2：Arrays VS Linked list-数组 VS 链表-
  - 3.3：Applicationg-应用-
- 4：小结Tips：

———————————————————————————————————————————————————————————-
————————————————————Hello算法—速通笔记—第二集—start———————–———————————————-

1：Understanding data structures ！

——了解数据结构——

1.1：Classification-分类-

常见的数据结构包括数组、链表、栈、队列、哈希表、树、堆、图，它们从 逻辑结构和物理结构 两个维度进行分类。

⚪ 逻辑结构揭示了数据元素之间的逻辑关系：

线性数据结构：数组、链表、栈、队列、哈希表，元素之间是一对一的顺序关系。
非线性数据结构：树、堆、图、哈希表。（进一步划分为树形结构和网状结构）
- 树形结构：树、堆、哈希表，元素之间是一对多的关系。
- 网状结构：图，元素之间是多对多的关系。

⚪ 物理结构反映了数据在计算机内存中的存储方式：

当算法程序运行时，正在处理的数据主要存储在内存中。
系统通过内存地址来访问目标位置的数据。
内存是所有程序的共享资源。因此在数据结构与算法的设计中，内存资源是一个重要的考虑因素。
所有数据结构都是基于数组、链表或二者的组合实现的。
例如，栈和队列既可以使用数组实现，也可以使用链表实现；而哈希表的实现可能同时包含数组和链表。
- 基于数组可实现：栈、队列、哈希表、树、堆、图、矩阵、张量（维度 >=3 的数组）等。
- 基于链表可实现：栈、队列、哈希表、树、堆、图等。

1.2：Type-类型-

基本数据类型：
是 CPU 可以直接进行运算的类型，在算法中直接被使用，主要包括以下几种。

整数类型 byte、short、int、long 。
浮点数类型 float、double ，用于表示小数。
字符类型 char ，用于表示各种语言的字母、标点符号甚至表情符号等。
布尔类型 bool ，用于表示“是”与“否”判断。

基本数据类型以二进制的形式存储在计算机中。
基本数据类型提供了数据的 内容类型，而数据结构提供了数据的 组织方式。

2：Arrays are the bricks that make up the wall of data structures *

——数组是组成数据结构这堵墙的一块块砖——

数组（array）是一种线性数据结构，其将相同类型的元素存储在连续的内存空间中。元素在数组中的位置称为该元素的索引（index）。

2.1：Common operations-常用操作-

1：初始化数组 2：访问元素 3：插入元素 4：删除元素 5：遍历数组 6：查找元素 7：扩容数组

代码示例：

/*1------ 初始化数组 */
int arr[5];
int nums[5] = { 1, 3, 2, 5, 4 };// 存储在栈上
int* arr1 = new int[5];// 存储在堆上（需要手动释放空间）
int* nums1 = new int[5] { 1, 3, 2, 5, 4 };

/*2------ 随机访问元素 */
int randomAccess(int *nums, int size) {
    int randomIndex = rand() % size;// 在区间 [0, size) 中随机抽取一个数字
    int randomNum = nums[randomIndex];// 获取并返回随机元素
    return randomNum;
}

/*3------ 在数组的索引 index 处插入元素 num */
void insert(int *nums, int size, int num, int index) {
    for (int i = size - 1; i > index; i--) {// 把索引 index 以及之后的所有元素向后移动一位
        nums[i] = nums[i - 1];
    }
    nums[index] = num;// 将 num 赋给 index 处的元素
}

/*4------ 删除索引 index 处的元素 */
void remove(int *nums, int size, int index) {
    for (int i = index; i < size - 1; i++) {// 把索引 index 之后的所有元素向前移动一位
        nums[i] = nums[i + 1];
    }
}

/*5------ 遍历数组 */
void traverse(int *nums, int size) {
    int count = 0;
    for (int i = 0; i < size; i++) {// 通过索引遍历数组
        count += nums[i];
    }
}

/*6------ 在数组中查找指定元素 */
int find(int *nums, int size, int target) {
    for (int i = 0; i < size; i++) {
        if (nums[i] == target)
            return i;
    }
    return -1;
}

/*7------ 扩展数组长度 */
int *extend(int *nums, int size, int enlarge) {
    int *res = new int[size + enlarge]; // 初始化一个扩展长度后的数组
    for (int i = 0; i < size; i++) {// 将原数组中的所有元素复制到新数组
        res[i] = nums[i];
    }
    delete[] nums;// 释放内存
    return res;// 返回扩展后的新数组
}

2.2：A&D-优缺点-

A—Advantages：

空间效率高：数组为数据分配了连续的内存块，无须额外的结构开销。
支持随机访问：数组允许在 O(1) 时间内访问任何元素。
缓存局部性：当访问数组元素时，计算机不仅会加载它，还会缓存其周围的其他数据，从而借助高速缓存来提升后续操作的执行速度。

连续空间存储是一把双刃剑。

D—Disadvantages：

插入与删除效率低：当数组中元素较多时，插入与删除操作需要移动大量的元素。
长度不可变：数组在初始化后长度就固定了，扩容数组开销很大。
空间浪费：如果数组分配的大小超过实际所需，多余的空间就被浪费。

2.3：Applicationg-应用-

随机访问：随机抽取一些样本，可以用数组存储，并生成一个随机序列，根据索引实现随机抽样。
排序和搜索：快速排序、归并排序、二分查找等都主要在数组上进行。
查找表：当需要快速查找一个元素或其对应关系时，可以使用数组作为查找表。
假如我们想实现字符到 ASCII 码的映射，则可以将字符的 ASCII 码值作为索引，对应的元素存放在数组中的对应位置。
机器学习：神经网络中大量使用了向量、矩阵、张量之间的线性代数运算，这些数据都是以数组的形式构建的。
数组是神经网络编程中最常使用的数据结构。
数据结构实现：数组可以用于实现栈、队列、哈希表、堆、图等数据结构。例如，图的邻接矩阵表示实际上是一个二维数组。

3：A linked list is a vine that shuttles between these bricks *

——链表是穿梭在这些砖块间的藤蔓——

链表（linked list）是一种线性数据结构，其中的每个元素都是一个节点对象，各个节点通过“引用”相连接。
链表的组成单位是节点（node）对象。每个节点都包含两项数据：节点的“值”和指向下一节点的“引用”。节点有头节点和尾节点。
尾节点指向的是“空”，在 Java、C++ 和 Python 中分别被记为 null、nullptr 和 None 。
链表节点 ListNode 除了包含值，还需额外保存一个引用（指针）。因此在相同数据量下，链表比数组占用更多的内存空间。

3.1：Common operations-常用操作-

1：初始化链表 2：插入节点 3：删除节点 4：访问节点 5：查找节点

代码示例：

/*1------ 初始化链表 1 -> 3 -> 2 -> 5 -> 4 */
ListNode* n0 = new ListNode(1);// 初始化各个节点
ListNode* n1 = new ListNode(3);
ListNode* n2 = new ListNode(2);
ListNode* n3 = new ListNode(5);
ListNode* n4 = new ListNode(4);
n0->next = n1;// 构建节点之间的引用
n1->next = n2;
n2->next = n3;
n3->next = n4;

/*2------ 在链表的节点 n0 之后插入节点 P ------只需改变两个节点引用（指针）即可*/
void insert(ListNode *n0, ListNode *P) {
    ListNode *n1 = n0->next;
    P->next = n1;
    n0->next = P;
}

/*3------ 删除链表的节点 n0 之后的首个节点 ------只需改变一个节点的引用（指针）即可*/
void remove(ListNode *n0) {
    if (n0->next == nullptr)
        return;
    ListNode *P = n0->next; // n0 -> P -> n1
    ListNode *n1 = P->next;
    n0->next = n1;
    delete P;// 释放内存
}

/*4------ 访问链表中索引为 index 的节点 ------在链表中访问节点的效率较低*/
ListNode *access(ListNode *head, int index) {
    for (int i = 0; i < index; i++) {
        if (head == nullptr)
            return nullptr;
        head = head->next;
    }
    return head;
}

/*5------ 在链表中查找值为 target 的首个节点 ------属于线性查找*/
int find(ListNode *head, int target) {
    int index = 0;
    while (head != nullptr) {
        if (head->val == target)
            return index;
        head = head->next;
        index++;
    }
    return -1;
}

3.2：Arrays VS Linked list-数组 VS 链表-

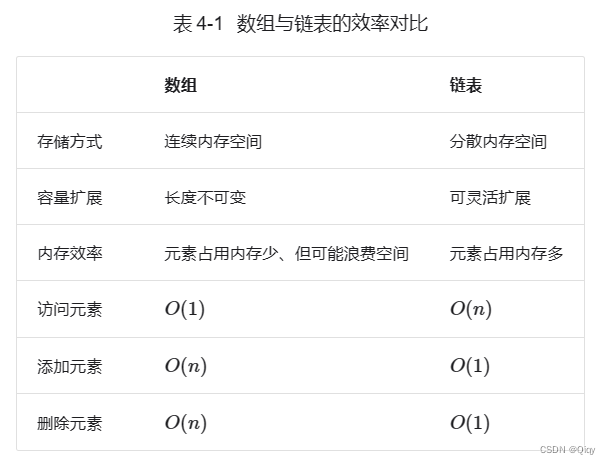
在这里插入图片描述

3.3：Applicationg-应用-

常见的链表类型包括三种：
单向链表：即普通链表。
环形链表：令单向链表的尾节点指向头节点（首尾相接），得到一个环形链表。其任意节点都可以视作头节点。
双向链表：与单向链表相比，双向链表记录了两个方向的引用。双向链表更灵活，可以朝两个方向遍历链表，但也占用更多的内存空间。

单向链表通常用于实现 栈、队列、哈希表和图等数据结构。
双向链表常用于需要快速查找前一个和后一个元素的场景。
- 高级数据结构：比如在红黑树、B 树中，我们需要访问节点的父节点，这可以通过在节点中保存一个指向父节点的引用来实现。
- 浏览器历史：在网页浏览器中，当用户点击前进或后退按钮时，浏览器需要知道用户访问过的前一个和后一个网页。
- LRU 算法：在缓存淘汰（LRU）算法中，我们需要快速找到最近最少使用的数据，以及支持快速添加和删除节点。
环形链表常用于需要周期性操作的场景，比如操作系统的资源调度。
- 时间片轮转调度算法在操作系统中，时间片轮转调度算法是一种常见的 CPU 调度算法，需要对一组进程进行循环。
- 数据缓冲区：在某些数据缓冲区的实现中，也可能会使用环形链表。