快速幂算法

参考视频(参考五角七边up大佬）

幂运算的介绍

幂运算是指将一个数自身乘以自身多次的运算，其表达式为 $a^n$，其中 $a$ 是底数，$n$ 是指数。

快速幂解释

快速幂算法是一种用于快速计算幂运算的算法，它利用了指数的二进制表示和幂运算的性质。通过将指数 $n$ 进行二进制拆分，可以将幂运算的时间复杂度降低到 $O(\log n)$。

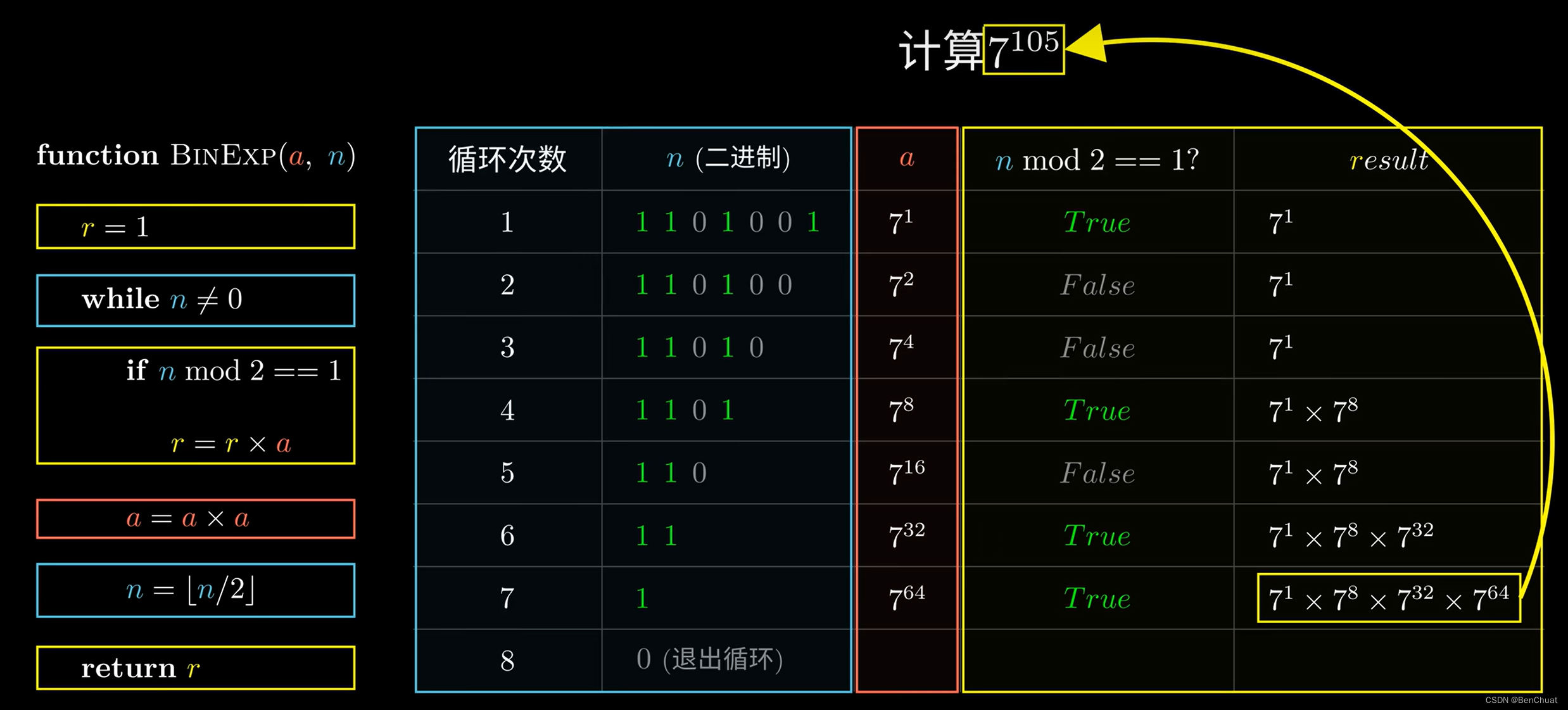
算法实现思路

快速幂算法的实现思路如下：

• 将指数 $n$ 转换为二进制形式。
• 从二进制形式的最低位开始遍历，每次将底数 $a$ 自乘，直到遍历完所有的二进制位。

Java代码实现

下面是快速幂算法的Java代码实现：

public class FastExponentiation {
    // 快速幂算法实现
    public static long fastExponentiation(long base, long exponent) {
        long result = 1;
        while (exponent > 0) {
            if (exponent % 2 == 1) {// 对2取余相当于”按位与“运算，exponent % 2 = exponent & 1
                result *= base;
            }
            base *= base;
            exponent /= 2;//除2向下取整相当于右移一位  exponent /= 2 相当于  exponent >>> 1
        }
        return result;
    }

    public static void main(String[] args) {
        // 测试
        long base = 2;
        long exponent = 10;
        System.out.println(base + " 的 " + exponent + " 次幂为：" + fastExponentiation(base, exponent));
    }
}

应用举例

问题描述

1. 幂取模运算：计算 $a^b\mathrm{mod}m$。
2. 计算斐波那契数列第 $n$ 项。
3. 将线性变换重复 $n$ 次。

运用快速幂算法解决思路分析

1. 幂取模运算：根据快速幂算法，先计算 $a^b$，然后对结果取模即可。
2. 计算斐波那契数列第 $n$ 项：利用斐波那契数列的递推关系 $F_{n+1}=F_n+F_{n-1}$，通过快速幂算法快速计算斐波那契矩阵的 $n$ 次幂。
3. 将线性变换重复 $n$ 次：通过快速幂算法，将线性变换的矩阵 $A$ 进行 $n$ 次幂运算，即 $A^n$。

代码设计思路

1. 幂取模运算：先利用快速幂算法求出幂运算结果，再对结果取模。
2. 计算斐波那契数列第 $n$ 项：利用快速幂算法求解斐波那契数列的矩阵快速幂，再取出结果矩阵的第一项即为第 $n$ 项的斐波那契数。
3. 将线性变换重复 $n$ 次：同样利用快速幂算法进行矩阵快速幂运算，得到最终的线性变换矩阵。

6. Java代码实现（应用举例）

下面是三个应用举例的Java代码实现：

public class FastExponentiationExamples {
    // 幂取模运算：计算 a^b % m
    public static long modularExponentiation(long base, long exponent, long modulus) {
        long result = 1;
        while (exponent > 0) {
            if (exponent % 2 == 1) {
                result = (result * base) % modulus;
            }
            base = (base * base) % modulus;
            exponent /= 2;
        }
        return result;
    }

    // 计算斐波那契数列第 n 项
    public static long fibonacci(int n) {
        long[][] matrix = {{1, 1}, {1, 0}};
        long[][] result = matrixPower(matrix, n - 1);
        return result[0][0];
    }

    // 矩阵快速幂
    public static long[][] matrixPower(long[][] matrix, int exponent) {
        int n = matrix.length;
        long[][] result = new long[n][n];
        for (int i = 0; i < n; i++) {
            result[i][i] = 1;
        }
        while (exponent > 0) {
            if (exponent % 2 == 1) {
                result = matrixMultiply(result, matrix);
            }
            matrix = matrixMultiply(matrix, matrix);
            exponent /= 2;
        }
        return result;
    }

    // 矩阵乘法
    public static long[][] matrixMultiply(long[][] A, long[][] B) {
        int n = A.length;
        long[][] result = new long[n][n];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                for (int k = 0; k < n; k++) {
                    result[i][j] += A[i][k] * B[k][j];
                }
            }
        }
        return result;
    }

    public static void main(String[] args) {
        // 测试
        long a = 3, b = 7, m = 1000000007;
        System.out.println("幂取模运算：" + a + "^" + b + " % " + m + " = " + modularExponentiation(a, b, m));

        int n = 10;
        System.out.println("斐波那契数列第 " + n + " 项：" + fibonacci(n));

        long[][] linearTransform = {{1, 1}, {0, 1}}; // 二维线性变换矩阵
        int repeat = 

5;
        long[][] resultMatrix = matrixPower(linearTransform, repeat);
        System.out.println("线性变换重复 " + repeat + " 次的结果矩阵：");
        for (int i = 0; i < resultMatrix.length; i++) {
            for (int j = 0; j < resultMatrix[0].length; j++) {
                System.out.print(resultMatrix[i][j] + " ");
            }
            System.out.println();
        }
    }
}