LeetCode-5. 最长回文子串【字符串 动态规划】
- 题目描述:
- 解题思路一:动态规划五部曲
- 解题思路二:动态规划[版本二]
- 解题思路三:0
题目描述:
给你一个字符串 s,找到 s 中最长的回文
子串
。
如果字符串的反序与原始字符串相同,则该字符串称为回文字符串。
示例 1:
输入:s = “babad”
输出:“bab”
解释:“aba” 同样是符合题意的答案。
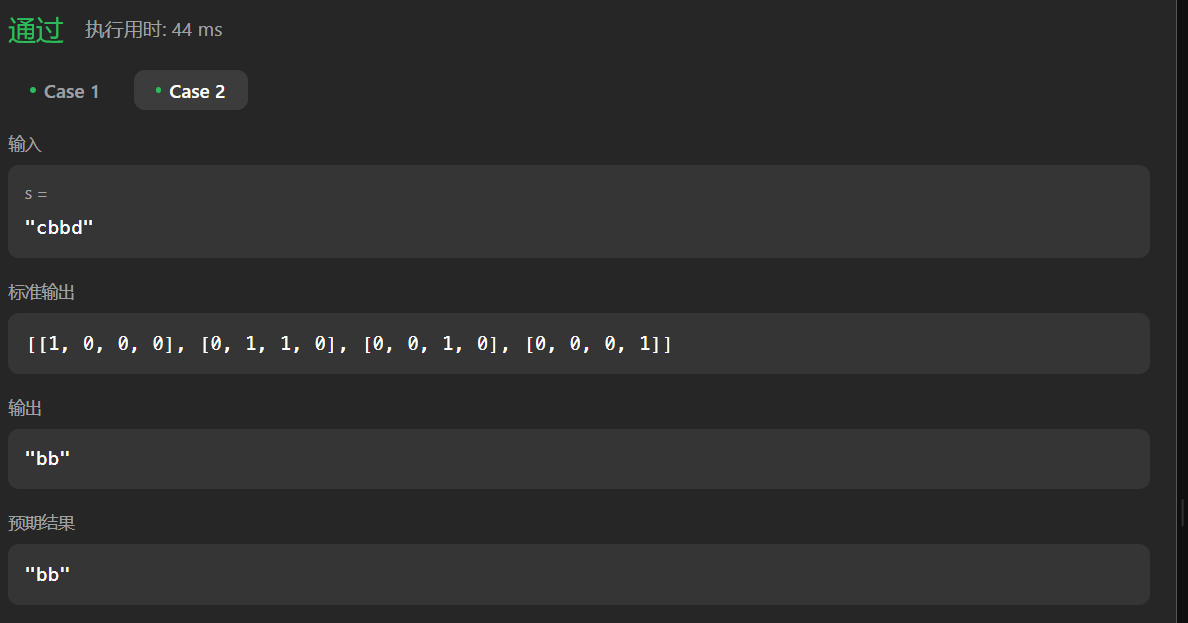
示例 2:
输入:s = “cbbd”
输出:“bb”
提示:
1 <= s.length <= 1000
s 仅由数字和英文字母组成
解题思路一:动态规划五部曲
-
定义dp[i][j]
dp[i][j] 表示 s[i…j] 是否是回文串 -
推导公式
当长度大于1,且s[i] == s[j]的时候才会更新dp数组
那么就是L的长度为2或者3(j - i < 3)并且 s[i] == s[j]可以直接确定dp[i][j] = 1
其他的就是状态转移方程:
dp[i][j] = dp[i+1][j-1]
- 初始化
dp = [[0] * n for _ in range(n)]
# dp[i][j] 表示 s[i..j] 是否是回文串
for i in range(n): # 长度为1必是回文串
dp[i][i] = 1
- 遍历顺序
先遍历字符串长度,后遍历左边界
for L in range(2, n+1):
# 枚举左边界,左边界的上限设置可以宽松一些
for i in range(n):
- 举例:
class Solution:
def longestPalindrome(self, s: str) -> str:
n = len(s)
if n < 2: return s
max_len, begin = 1,0
dp = [[0] * n for _ in range(n)]
# dp[i][j] 表示 s[i..j] 是否是回文串
for i in range(n): # 长度为1必是回文串
dp[i][i] = 1
# 先枚举子串长度
for L in range(2, n+1):
# 枚举左边界,左边界的上限设置可以宽松一些
for i in range(n):
j = L + i - 1 # # 由 L 和 i 可以确定右边界
if j >= n: break # 如果右边界越界,就可以退出当前循环
if s[i] == s[j]:
if j - i < 3:
dp[i][j] = 1
else:
dp[i][j] = dp[i+1][j-1]
if dp[i][j] and L > max_len: # 只要 dp[i][L] == true 成立,就表示子串 s[i..L] 是回文,此时记录回文长度和起始位置
max_len = L
begin = i
return s[begin: begin + max_len]
时间复杂度:O(n2)
空间复杂度:O(n2)
解题思路二:动态规划[版本二]
class Solution:
def longestPalindrome(self, s: str) -> str:
n = len(s)
dp = [[0] * n for _ in range(n)]
begin, max_len = 0, 1
for i in range(n):
dp[i][i] = 1
for L in range(2, n+1):
for i in range(n):
j = L + i - 1
if j >= n:
break
if s[i] == s[j]:
if j - i < 3:
dp[i][j] = 1
else:
dp[i][j] = dp[i+1][j-1]
if dp[i][j] and L > max_len:
begin = i
max_len = L
return s[begin: begin + max_len]
时间复杂度:O(n2)
空间复杂度:O(n2)
解题思路三:0
时间复杂度:O(n)
空间复杂度:O(n)