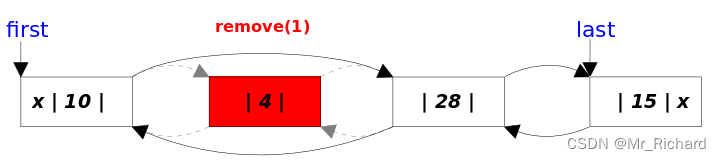
目录
4 椭圆曲线:更好的陷门函数
5 奇异的对称性
6 让我们变得奇特
⚠️ 原文地址:A (Relatively Easy To Understand) Primer on Elliptic Curve Cryptography
⚠️ 写在前面:本文属搬运博客,自己留着学习。如果你和我一样是小白,那么看完本文我们将仍然不能理解下图具体是在干什么,但能够对 RSA 和椭圆曲线加密的初衷有所了解。

密码学 | 椭圆曲线 ECC 密码学入门(一)文章浏览阅读273次,点赞4次,收藏8次。1 公共密钥密码学的兴起2 玩具版 RSA 算法2.1 RSA 基本原理2.2 RSA 举例说明1 加密2 解密3 不是完美的陷门函数https://blog.csdn.net/m0_64140451/article/details/137672818?spm=1001.2014.3001.5502
4 椭圆曲线:更好的陷门函数
在 RSA 和 Diffie-Hellman 算法被提出之后,研究人员开始探索其他基于数学的密码学解决方案,寻找超越因式分解的其他算法,这些算法可以作为良好的陷门函数。1985 年,基于一种深奥的数学分支 —— 椭圆曲线的密码学算法被提出。
但椭圆曲线究竟是什么,以及其背后的陷门函数是如何工作的呢?不幸的是,与因式分解不同 —— 我们中学生在初中第一次接触到 —— 大多数人对椭圆曲线的数学并不熟悉。数学并不简单,解释起来也不容易,但我会尝试在接下来的几部分中解释。
如果您的眼睛开始变得模糊,您可以跳到最后一部分:“这一切意味着什么?”
椭圆曲线是满足特定数学方程的点的集合。椭圆曲线的方程看起来像这样:
这个方程定义了一个椭圆曲线,而椭圆曲线具有一系列独特的数学性质,这些性质对密码学家来说非常有兴趣。这个方程的图像如下:

椭圆曲线的其他表示方法有很多,但技术上讲,椭圆曲线是满足两个变量中一个变量的二次方程和另一个变量的三次方程的点的集合。椭圆曲线不仅仅是一张漂亮的图片,它还有一些特性,使它成为密码学的一个良好环境。
5 奇异的对称性
仔细观察上面绘制的椭圆曲线。它有几个有趣的特性。
- 其中之一是 水平对称性。曲线上的任何点都可以关于 x 轴反射而仍留在同一曲线上。
- 更有趣的特性是,任何非垂直线将与曲线 最多相交三个点。
让我们将这个曲线想象成一个奇怪的台球游戏的场景。

如上图所示,取曲线上任意两点并画一条通过它们的线,它会恰好再与曲线相交一个点。在这个台球游戏中,你在点 A 处取一个球,向点 B 射击。当球碰到曲线时,球会要么直接向上(如果它在 x 轴下方)要么直接向下(如果它在 x 轴上方)弹跳到曲线的另一侧。
为什么比喻为台球?答:因为在台球运动中,台球撞击到桌子的边沿会反弹。不过现实中的台球反弹方向有无穷多种,而这里的台球只会向上或向下反弹。
我们可以称这种在两点上的台球移动为 “dot” 。曲线上的任何两点都可以 “dot” 在一起得到一个新点。比如:
- A dot B = C
个人认为,这里把 “dot” 理解成一种自定义的运算就行了(可以按个人喜好起名),类似于小学做的定义新运算题。
我们也可以将台球的移动串联起来,即不断地用 “dot” 操作一个点与自己。
- A dot A = B
- A dot B = C
- A dot C = D
- ……
这里的意思是:假设初始点是 A,然后让 A 不断和自己做 “dot” 运算。
结果证明,如果你有两个点,一个初始点与自己点运算 n 次后到达一个最终点,而你只知道最终点和第一个点,要找出 n 是困难的。
这里的意思是:假设只告诉你初始点 A 和它最终到达的点 Z,那么你很难求出该过程中做了多少次 “dot” 运算,即求解 n 的值非常困难。
为了继续我们奇怪的台球比喻,想象有一个人在一个房间里独自玩我们的游戏一段时间。他很容易按照上述规则一次又一次地击球。如果稍后有人走进房间,看到球最终停在了哪里,即使他们知道所有的游戏规则和球开始的地点,他们也无法确定球被击打了多少次才能到达那里,除非他们再次重新经历整个游戏,直到球到达同一个点。容易做到,难以撤销:这就是一个非常好的陷门函数的基础。
椭圆曲线算法也满足 “单向容易,逆向困难”,其中单向是做 “dot” 运算,逆向是求解 n 的值。套用台球的比喻就是,单向是击球,逆向是求解击了多少次球。
6 让我们变得奇特
这个翻译确实很奇特。。。
上面简化后的曲线非常适合观赏和解释椭圆曲线的概念,但它并不代表用于密码学的曲线的样子。为此,我们必须限制自己在一定范围内的数字,就像在 RSA 中那样。我们不是允许曲线上的点有任何值,而是限制自己在固定范围内的整数。
在计算椭圆曲线公式时,我们使用同样的技巧,当达到最大值时将数字循环。如果我们选择最大值为一个素数,那么椭圆曲线被称为 素数曲线,并具有优秀的密码学特性。
所谓 “数字循环” 也还是取模的意思。假设最大值是 8,当我们数到 8 后又回到 1 这个起点,形成原文所说的数字循环:1, 2, ..., 7, 8, 1, 2, ..., 7, 8, 1, 2, ... 。
下面是一个椭圆曲线对于所有数字的绘图示例:

下面是同一条曲线,但只用整数点表示,最大值为 97 的绘图:

这看起来一点也不像传统意义上的曲线,但实际上它就是。就像原始曲线在边缘被包裹起来,只有那些触及整数坐标的曲线部分被着色。你甚至仍然可以观察到水平的对称性。
竖着一列一列地看,这些点确实是关于 x 轴对称的。
事实上,你仍然可以在这条曲线上玩台球游戏,并且可以将点相互 “dot” 在一起。曲线上的直线方程仍然具有相同的性质。此外,这种 “dot” 操作可以有效地计算。
个人理解,简单来说:假设你选择了曲线上一点 A 作为初始点,并且让它不断和自己做 “dot” 运算,中途会到达 B、C、D 等点,最后你会发现 n 次运算后又会回到 A 点。由此可以认为,A 以及 B、C、D 等点的集合构成了这条椭圆曲线。因此原文说 “同一条曲线,但只用整数点(就可以)表示”。
你可以将两点之间的线想象成一条在边界处环绕直到触及一点的线。仿佛在我们的奇怪台球游戏中,当球击中桌子的边缘(最大值 max)时,它就会神奇地被传送到桌子的另一侧,并继续它的路径直到触及一个点。

在这种新的曲线表示方法中,你可以把一些消息表示为曲线上的若干个点。你可以想象取出一个消息并将其设置为 x 坐标,然后解出 y 以得到曲线上的一个点。在实际中,这个过程比这略微复杂一些,但这是大概的想法。
你会得到以下点:
(70,6), (76,48), ……, (82,6), (69,22)
这一小段讲得确实比较抽象,不知道是不是翻译的原因。
椭圆曲线密码系统可以通过选择一个素数作为最大值、一个曲线方程和曲线上的一个公共点来定义。私钥是一个数字 priv,公钥是公共点与自身相乘 priv 次的结果。在这种密码系统中,从公钥计算私钥的过程被称为 椭圆曲线离散对数函数。这最终是我们一直在寻找的 “陷门函数”。
个人理解:“公共点” 可以理解为前文中提到的起始点 A 点,“相乘” 实际上应该是指前文定义的 “dot” 运算。最后这段话应该算是本文的核心了🥳