前记
在群体基因组学研究中，我们常常需要知道一些位点的变异情况，以便于根据对应的表型信息估算这些位点的效应，同时了解这些位点在不同亚群之间的变化情况。这个时候我们就需要进行单倍型分析(Haplotype Analysis)，单倍型分析是研究基因组中特定区域的单倍型状态的方法，通过确定个体的单倍型组合及其频率，了解基因座间的关联性以及对特定性状影响。
geneHapR是2023年发布的一款可用于单倍型分析的R包，由中国农业科学院刁现民老师课题组开发，发表于BMC旗下Bioinformatics期刊，该包的使用方法较为简单，适用于新手入门分析。
本文以vcf文件为例，演示如何进行单倍型分析。
一、geneHap包简介
1、geneHap的工作流程
如下图所示，可以看到，用户需要准备的包括：基因型文件、注释文件和样本信息文件，以及后续会用的表型文件。输出的主要内容有：变异位点的可视化、单倍型网络、地理分布、表型比较和连锁不平衡热图。
2、geneHapR的安装
打开R或Rstudio，输入以下代码进行安装：
library(BiocManager)
BiocManager::install(c("Biostrings", "GenomicRanges", "muscle",
"IRanges", "rtracklayer", "trackViewer"))
install.packages("geneHapR")
library(geneHapR)二、输入文件的设置
需事先查询好目的基因的物理位置信息，使用bcftools工具提取目的基因的vcf变异信息文件，代码如下：
#bcftools将vcf生成bgzip和index格式
bcftools view my.vcf -Oz -o my.vcf.b.gz
bcftools index my.vcf.b.gz
#提取基因的vcf文件
bcftools filter my.vcf.b.gz --regions chr1:3478748-3480748 > mygene.vcf
在R中读取该文件：
vcf <- import_vcf("mygene.vcf")单纯地进行基因的单倍型分析（即获取基因的不同单倍型分类情况），只需基因的vcf文件！
三、进行单倍型分析
R或Rstudio，输入以下代码：
library(geneHapR)
setwd("D:/Working-Folder/R-work/geneHapR/")
vcf <- import_vcf("mygene.vcf")
geneID <- "mygene" # 基因ID
Chr <- "num" # 基因所处的染色体名称
start <- start # 基因的起始位置（染色体坐标）
end <- end # 基因的终止位置（染色体坐标）
hapPrefix <- "Hap" # 单倍型名称的前缀
# 从VCF开始单倍型鉴定
hapResult <- vcf2hap(vcf, hapPrefix = hapPrefix,
hetero_remove = TRUE, # 移除包含杂合位点的样本
na_drop = TRUE) # 移除包含基因型缺失的样本
# 对单倍型结果进行汇总整理
hapSummary <- hap_summary(hapResult, hapPrefix = hapPrefix)
# 将单倍型鉴定结果保存到硬盘
write.hap(hapResult, file = "mygene.hapResult")
write.hap(hapSummary, file = "mygene.hapSummary")
# 导入之前的单倍型分析结果
hapResult <- import_hap(file = "mygene.hapResult")
hapSummary <- import_hap(file = "mygene.hapSummary")
# 以表格形式展示各单倍型的基因型
plotHapTable(hapSummary, # 单倍型结果
hapPrefix = hapPrefix, # 单倍型名称前缀
angle = 45, # 物理位置的角度
displayIndelSize = 0, # 图中展示最大的Indel大小
title = geneID) # 图片标题运行结束后，会产生一个表格型图片，显示该基因的单倍型信息。
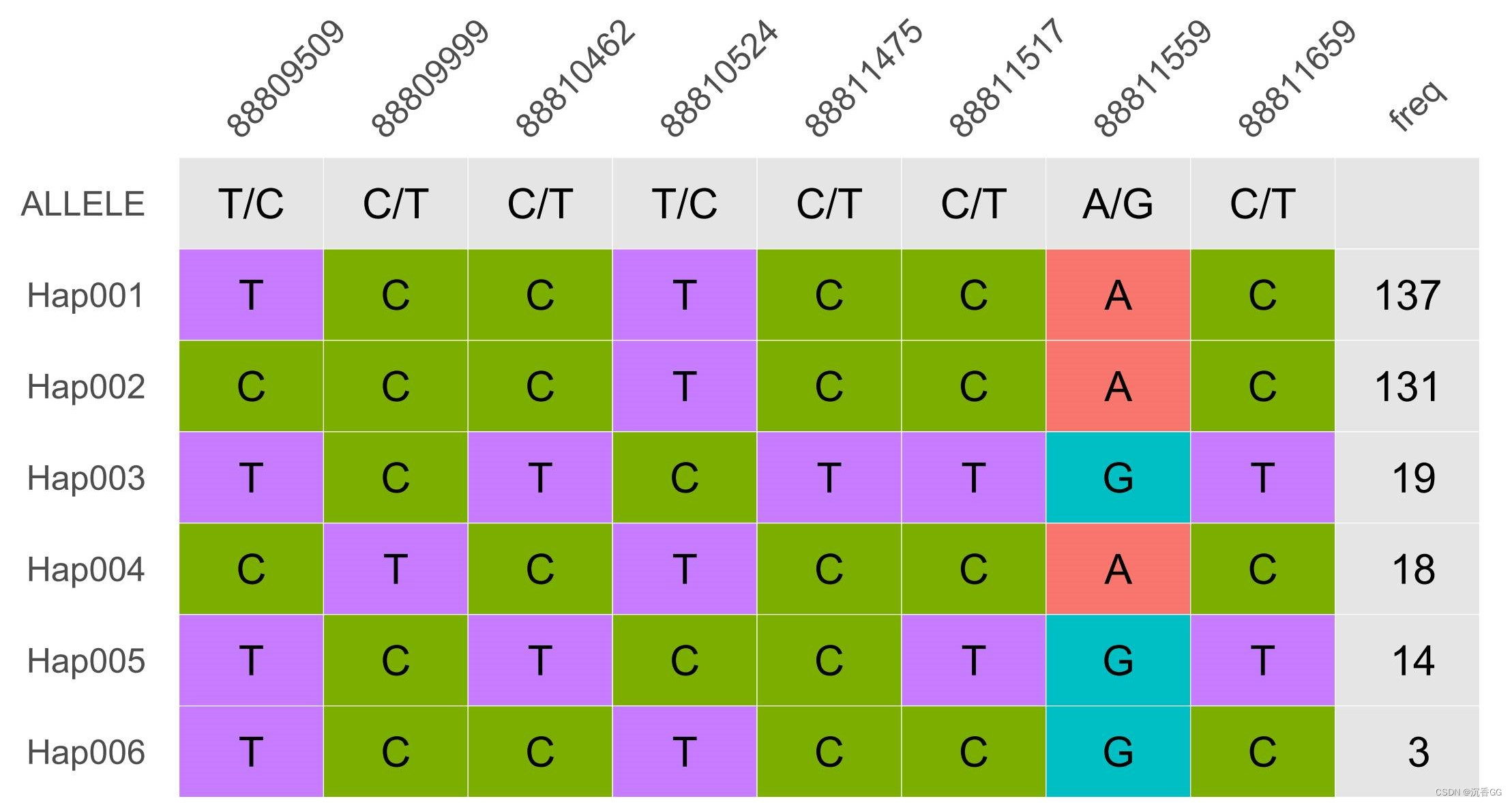
可以看到，该基因有6种单倍型，最后面一列是每种单倍型对应的样本数目。
四、优异单倍型挖掘
获取单倍型及对应的样本信息后，再结合对应的表型，进行多重比较，即可获知哪一种单倍型的表型最好。此过程可在Excel活GraphPad Prism等软件进行，过程较为简单，在此不再演示。
五、参考信息
geneHapR做基因单倍型分析-CSDN博客
https://blog.csdn.net/zhang_rl/article/details/130831155
GitHub - ZhangRenL/geneHapRContribute to ZhangRenL/geneHapR development by creating an account on GitHub.https://github.com/ZhangRenL/geneHapRgeneHapR: an R package for gene haplotypic statistics and visualization | BMC Bioinformatics | Full Text (biomedcentral.com)https://bmcbioinformatics.biomedcentral.com/articles/10.1186/s12859-023-05318-9
后记
以上是简单使用geneHapR包进行单倍型分析的操作，后续讲述该包的其它功能（基因结构、LD分析、单倍型网络和地理分布等）。
--------2024.4.12
--------CXGG
千里之行，始于足下。
