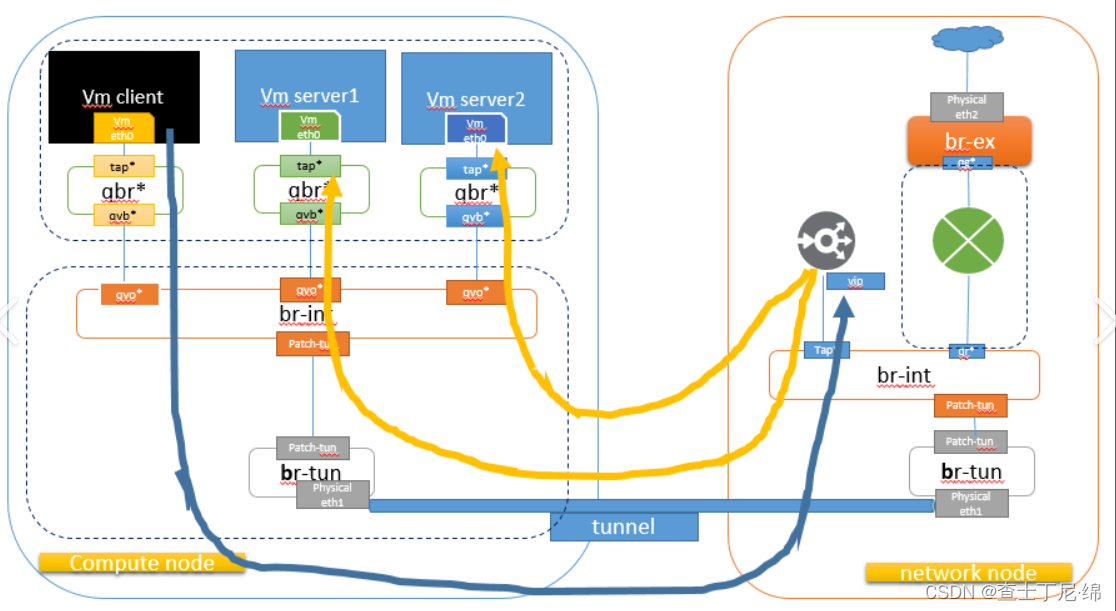
标量、向量、张量
- 标量占据的是零维空间
- 向量占据的是一维数据,例如语音信号
- 矩阵占据的是二维数组,例如灰度图像
- 张量占据的是三维乃至更高维的数组,例如RGB图像和视频
内积(点乘)概述
内积(inner product) 计算的则是两个向量之间的关系
两个相同维度向量内积的表达式为: 
。 即对应元素乘积的求和
内积能够表示两个向量之间的相对位置,即向量之间的夹角。一种特殊的情况是内积为0,即(X, Y) = 0,,在二维空间上,这意味两个向量的夹角为90度,互相垂直
而在高维空间上,这种关系被称为正交(orthogonality)。如果两个向量正交,说明他们线性无关,相互独立,互不影响
正交基
如果有一个集合,它的元素都是具有相同维数的向量(可以是有限个或无限个),并且定义了加法和数乘等结构化的运算,这样的集合就称为线性空间(liner space),定义了内积运算的线性空间则被称为内积空间(inner product space)
在内积空间中,一组两两正交的向量构成这个空间的正交基(orthogonal basis),假若正交基中基向量的L2范数都是单位长度1,这组正交基就是标准正交基(orthonormal basis)
例子:在三维空间中,我们可以使用标准单位向量作为正交基,即:
i
=
[
1
0
0
]
,
j
=
[
0
1
0
]
,
k
=
[
0
0
1
]
\mathbf{i} = \begin{bmatrix} 1 \ 0 \ 0 \end{bmatrix}, \quad \mathbf{j} = \begin{bmatrix} 0 \ 1 \ 0 \end{bmatrix}, \quad \mathbf{k} = \begin{bmatrix} 0 \ 0 \ 1 \end{bmatrix}
i=[1 0 0],j=[0 1 0],k=[0 0 1]
这些向量两两之间的内积为零,即
i
⋅
j
=
i
⋅
k
=
j
⋅
k
=
0
\mathbf{i} \cdot \mathbf{j} = \mathbf{i} \cdot \mathbf{k} = \mathbf{j} \cdot \mathbf{k} = 0
i⋅j=i⋅k=j⋅k=0,并且它们的长度都是1,因此它们是标准正交基。
在更高维的空间中,比如四维空间,一个正交基可以是:
e
1
=
[
1
0
0
0
]
,
e
2
=
[
0
1
0
0
]
,
e
3
=
[
0
0
1
0
]
,
e
4
=
[
0
0
0
1
]
\mathbf{e_1} = \begin{bmatrix} 1 \ 0 \ 0 \ 0 \end{bmatrix}, \quad \mathbf{e_2} = \begin{bmatrix} 0 \ 1 \ 0 \ 0 \end{bmatrix}, \quad \mathbf{e_3} = \begin{bmatrix} 0 \ 0 \ 1 \ 0 \end{bmatrix}, \quad \mathbf{e_4} = \begin{bmatrix} 0 \ 0 \ 0 \ 1 \end{bmatrix}
e1=[1 0 0 0],e2=[0 1 0 0],e3=[0 0 1 0],e4=[0 0 0 1]
这些向量同样是两两正交的,并且长度为1,因此它们构成了四维空间的正交基。
线性变换
在数学和物理学中,当我们描述一个点在空间中移动时,可以用向量来表示这个点的位置
如果这个点从一个位置移动到另一个位置,那么表示这个点位置的向量也会随之改变。这种改变可以通过一种数学工具–矩阵来实现,这种改变称为线性变换
线性变换具有以下特点:
- 向量经过线性变换后,其坐标按照一定的数学规则进行变换
- 线性变换保持向量之间的线性关系,例如,线性变换前后,两个向量的和的变换等于它们各自变换后的和
转置矩阵
转置矩阵是指将原矩阵的行和列进行相互得到的新矩阵
转置矩阵的作用:
- 坐标变换: 在计算机图形学中,转置矩阵常用于变换坐标系统。例如,当一个物体的坐标需要根据相机或观察者的角度进行变化时-
- 简化计算: 在解线性方程组时,转置矩阵可以用来简化计算过程,特别是在使用行列式和逆矩阵时
- 矩阵乘法: 当需要计算两个矩阵的乘积时,转置矩阵的概念很有用,因为
(AB)^{T} = B^{T}A^{T},这个性质有时可以减少计算量
原矩阵:
tensor([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11],
[12, 13, 14, 15],
[16, 17, 18, 19]])
转置矩阵:
tensor([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11],
[12, 13, 14, 15],
[16, 17, 18, 19]])
逆矩阵
逆矩阵是指对于给定的方阵(行数和列数相等的矩阵)X,存在另一个矩阵X^-1,使得两者相乘的结果等于单位矩阵I。数学上表示为
X
⋅
X
−
1
=
X
−
1
⋅
X
=
I
X \cdot X^{-1} = X^{-1} \cdot X = I
X⋅X−1=X−1⋅X=I
对称矩阵(symmetric matrix)
对称矩阵是指一个方阵,其行和列数量相等,且满足
X = X T X = X^{T} X=XT

B = torch.tensor([[1, 2, 3], [2, 0, 4], [3, 4, 5]])
B
tensor([[1, 2, 3],
[2, 0, 4],
[3, 4, 5]])
B == B.T
tensor([[True, True, True],
[True, True, True],
[True, True, True]])
特征值(eigenvalue)和特征向量(eigenvector)
描述矩阵的一对重要参数是特征值(eigenvalue) 和 特征向量(eigenvector). 对于给定的矩阵A,假设其特征值是λ,特征向量为x,它们的关系为:

矩阵代表了向量的变换,其效果通常对原始向量同时施加方向变化和尺度变化
如果一个矩阵只能伸缩一个向量,并不能改变向量的方向,那么这个向量就是矩阵的特征向量。特征是衡量事物的各个维度或者尺度,如果不停变化也就称不上特征了
矩阵特征值和特征向量的动态意义在于表示了变化的速度和方向。如果把矩阵所代表的变化看作奔跑的人,那么矩阵的特征值就代表了他奔跑的速度,特征向量代表了他奔跑的方向
奇异值分解
求解给定矩阵的特征值和特征向量的过程叫做特征值分解,但能够进行特征值分解的矩阵必须是 n 维方阵
范数
范数(norm) 是对单个向量大小的度量,描述的是向量自身的性质,其作用是将向量映射为一个非负的数值
通用的 L^p 范数定义如下:

对一个给定向量
- L^1 范数计算的是向量所有元素绝对值的和
- L^2范数计算的是通常意义上的向量长度
- L^∞ 范数计算的则是向量中最大元素的取值
范数计算的是单个向量的尺度,内积(inner product)计算的则是两个向量的关系
代码实现
内积例子
import numpy as np
A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])
inner_product = np.sum(A.T * B)
print(inner_product) # 输出结果应该是70
正交基例子
在三维空间中,可以通过经度、纬度、和海拔高度来确定一个确切的位置,因为这三个坐标轴构成一套明确的参考系。
然而,当我们进入更高维的空间时,这种直观的坐标系定义就不再适用了,因为高维空间超出了我们的直观感知
在高维空间中,使用正交基来确定位置,这是因为正交基能够为空间提供一套可以量化和计算坐标的系统
正交基是一组两两正交的向量,它们可以定义高维空间中的“经纬度”, 如果这些向量还是标准正交基(即长度为1),那么它们可以更方便地用于表示和计算点在空间中的位置
import numpy as np
# 假设我们有以下的标准正交基,这里以三维空间为例
# 注意:实际使用中,正交基的数量应与空间的维度一致
orthogonal_basis = np.array([
[1, 0, 0], # x轴方向的基向量
[0, 1, 0], # y轴方向的基向量
[0, 0, 1] # z轴方向的基向量
])
# 我们要表示的点的坐标,这里以三维空间中的一个点为例
point_coordinates = np.array([2, 3, 4]) # (x, y, z)坐标
# 使用正交基来表示这个点
# 这可以通过点乘正交基和点的坐标来实现
point_representation = np.dot(orthogonal_basis.T, point_coordinates)
print("点的表示(按照正交基展开的坐标):", point_representation)
线性变换
import numpy as np
# 定义一个点P在二维空间中的初始位置,用向量表示
point_p = np.array([2, 3]) # 向量 [2, 3]
# 定义一个线性变换矩阵A,例如旋转变换
# 这里我们定义一个旋转90度的变换矩阵
transform_matrix_a = np.array([[0, -1], # 旋转变换矩阵
[1, 0]])
# 应用线性变换,计算点P变换后的位置
transformed_point_p = np.dot(transform_matrix_a, point_p)
print("变换前的点P坐标:", point_p)
print("变换后的点P坐标:", transformed_point_p)
矩阵的作用就是对正交基进行变换
矩阵可以用来改变空间中的参考框架,特别是当这个参考框架由正交基组成
正交基是一组相互垂直(在二维空间中是90度角,在高维空间中是相互点乘为0)的向量,它们定义了一个空间结构
当我们有一个向量在一个由正交基定义的空间中,通过左乘一个矩阵,我们可以将这个向量转换到另一个由不同正交基定义的空间中。这个矩阵定义了这两个空间之间的变换
import numpy as np
# 定义原始的正交基,这里以二维空间为例
b1 = np.array([1, 0])
b2 = np.array([0, 1])
# 打印原始基
print("原始正交基:")
print("b1 =", b1)
print("b2 =", b2)
# 定义一个变换矩阵,例如一个45度的旋转矩阵
theta = np.pi / 4 # 45度
A = np.array([[np.cos(theta), -np.sin(theta)],
[np.sin(theta), np.cos(theta)]])
# 应用变换矩阵到原始基上
b1_transformed = A.dot(b1)
b2_transformed = A.dot(b2)
# 打印变换后的基
print("\n变换后的正交基:")
print("b1_transformed =", b1_transformed)
print("b2_transformed =", b2_transformed)
特征向量例子
在一个线性变换中,如果一个矩阵对一个向量仅产生伸缩效果,而不会改变该向量的方向,那么这个向量被称为该矩阵的特征向量。
对于矩阵 ( A ) 和一个非零向量 ( v ),如果存在一个标量 ( lambda ) 使得 ( Av = lambda v ),那么 ( v ) 就是矩阵 ( A ) 的特征向量,对应的 ( lambda ) 是特征值
import numpy as np
# 定义一个矩阵 A
A = np.array([[4, 1], [2, 3]])
# 使用 NumPy 的 eig() 函数计算特征值和特征向量
eigenvalues, eigenvectors = np.linalg.eig(A)
print("特征值:", eigenvalues)
print("特征向量:\n", eigenvectors)
# 特征向量与特征值的验证
for i in range(len(eigenvalues)):
v = eigenvectors[:, i]
lambda_v = eigenvalues[i] * v
Av = np.dot(A, v)
print("验证特征向量 {} 和特征值 {}: \nA*v = {} \nlambda*v = {}".format(i+1, eigenvalues[i], Av, lambda_v))
在这个代码中,我们定义了一个矩阵 A,然后使用 np.linalg.eig() 函数来计算特征值和特征向量
输出将显示特征值和对应的特征向量,同时代码中的循环还对计算结果进行了验证,确保 ( Av ) 等于 ( \lambda v )
这表明,对于这些特征向量,矩阵 A 仅进行了伸缩变换,而没有改变它们的方向
转置矩阵例子
import numpy as np
# 创建一个4x3的矩阵A
A = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9],
[10, 11, 12]])
# 转置矩阵A
A_T = np.transpose(A)
print("Original Matrix A:")
print(A)
print("\nTransposed Matrix A_T:")
print(A_T)
# 假设我们有一个向量v,我们想要计算A和v的点积
v = np.array([1, 0, 1])
# 使用A_T来计算点积,这实际上是对A的列向量进行点积操作
result = np.dot(A_T, v)
print("\nResult of A_T * v:")
print(result)
在这个例子中,我们创建了一个4x3的矩阵A,并计算了它的转置A_T。然后,我们使用转置矩阵A_T和向量v进行点积运算
逆函数例子
用2 * 2矩阵A来解释一些逆矩阵的算法。首先,交换a11和a22 位置,然后在a12 和 a21前加上负号,最后除以行列式a11a22 - a12a21
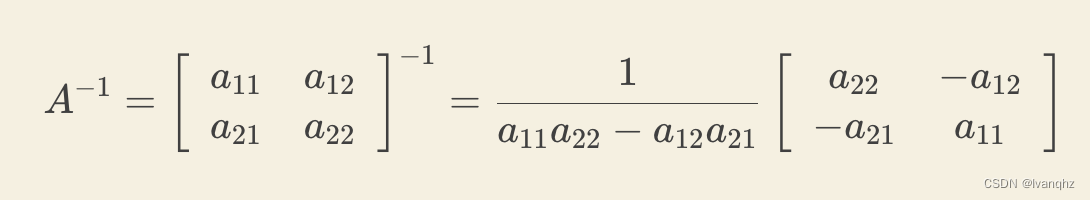
如何验证是不是正解?
方法很简单,
A
⋅
A
−
1
=
A
−
1
⋅
A
=
I
A \cdot A^{-1} = A^{-1} \cdot A = I
A⋅A−1=A−1⋅A=I
现在代入公式来验证,A和它的逆矩阵相乘



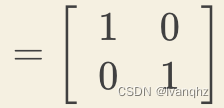
范数的例子
‘范数计算的是单个向量的尺度’,意思是,范数是用来衡量向量在某个向量空间中的长度或大小
范数给出一个数值,表示向量相对于其他向量的长度或大小
考虑一个二维空间中的向量 x = [3, 4],我们可以使用L2范数(也称为欧几里得范数或向量模)来计算这个向量的长度
∣
x
∣
2
=
3
2
+
4
2
=
9
+
16
=
25
=
5
|x|_2 = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5
∣x∣2=32+42=9+16=25=5
这意味着向量 x 在二维空间中的长度为5。 L2范数是最常见的范数之一,它对应于向量在几何上的直观长度
另一个例子,使用L1范数(也称为曼哈顿范数)来计算同样的向量 x:
∣
x
∣
1
=
∣
3
∣
+
∣
4
∣
=
3
+
4
=
7
|x|_1 = |3| + |4| = 3 + 4 = 7
∣x∣1=∣3∣+∣4∣=3+4=7
这里,L1范数给出了向量在各个维度上绝对值的和,即7。L1范数在某些情况下更有用,比如在稀疏数据处理中
参考资料
- 特征值和特征向量到底是个啥?能做什么用?
- 通俗易懂:对称矩阵