1.分类问题

从回归到多类分类：对类别进行一位有效编码——独热编码（one-hot encoding）。独热编码是一个向量，它的分量和类别一样多。类别对应的分量设置为1，其他所有分量设置为0：
$\begin{aligned} & \mathbf{y}=\left[y_1, y_2, \ldots, y_n\right]^{\top} \\ & y_i=\left\{\begin{array}{l} 1 \text { if } i=y \\ 0 \text { otherwise } \end{array}\right. \end{aligned}$

2. 网络架构

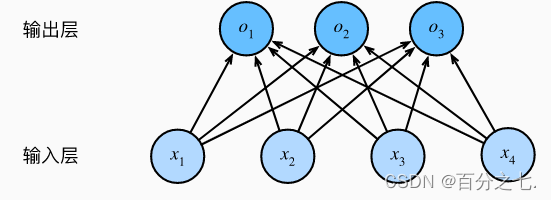
为了估计所有可能类别的条件概率，我们需要一个有多个输出的模型，每个类别对应一个输出。
与线性回归一样，softmax回归也是一个单层神经网络。由于计算每个输出取决于所有输入，所以softmax回归的输出层也是全连接层。
在这里插入图片描述

3.softmax运算

我们希望模型的输出可以视为属于类的概率，然后选择具有最大输出值的类别作为我们的预测类。
然而我们能否将未规范化的预测值直接视作我们感兴趣的输出呢？答案是否定的。因为将线性层的输出直接视为概率时存在一些问题：一方面，我们没有限制这些输出数字的总和为1。另一方面，根据输入的不同，它们可以为负值。
那么要将输出视为概率，我们必须保证在任何数据上的输出都是非负的且总和为1。softmax函数正是这样做的： softmax函数能够将未规范化的预测变换为非负数并且总和为1，同时让模型保持可导的性质。为了完成这一目标，我们首先对每个未规范化的预测求幂，这样可以确保输出非负。为了确保最终输出的概率值总和为1，我们再让每个求幂后的结果除以它们的总和。如下式：
$\hat{\mathbf{y}}=\operatorname{softmax}(\mathbf{o}) \quad \text { 其中 } \quad \hat{y}_j=\frac{\exp \left(o_j\right)}{\sum_k \exp \left(o_k\right)}$ 尽管softmax是一个非线性函数，但softmax回归的输出仍然由输入特征的仿射变换决定。因此，softmax回归是一个线性模型（linear model）。