三、假定我们不仅对计数器进行增 1 操作,还会进行置 0 操作(即将所有位复位)。设检测或修改一个位的时间为 Θ(1) ,说明如何用一个位数组来实现计数器,使得对一个初值为 0 的计数器执行一个由任意 n 个 INCREMENT 和 RESET 操作组成的序列花费时间 O(n) 。(提示:维护一个指针一直指向最高位的 1 。)
文心一言:
为了实现这样一个计数器,我们可以使用一个位数组(bit array)来存储计数器的当前值,并维护一个额外的指针来指向最高位的 1。每次执行 INCREMENT 或 RESET 操作时,我们可以利用这个指针来高效地更新计数器。
下面是具体实现的步骤:
初始化:
创建一个足够大的位数组(bit array)来存储计数器的值。假设位数组的大小为 m。
初始化所有位为 0。
初始化一个指针 highestOne,指向位数组的起始位置(即最低位)。
INCREMENT 操作:
如果 highestOne 指向的位是 0,则将该位设置为 1,并返回。
否则,从 highestOne 指向的位开始,向右遍历位数组,直到找到一个 0 或者到达位数组的末尾。
如果找到一个 0,将其设置为 1,并更新 highestOne 指向这个新设置的 1。
如果到达位数组的末尾,则需要进位。此时,将 highestOne 指向的位重置为 0,并向右移动一位。如果到达位数组的末尾仍然需要进位,则扩展位数组的大小,并在新扩展的位上设置 1。更新 highestOne 指向新设置的 1。
RESET 操作:
将位数组中的所有位都设置为 0。
将 highestOne 指针重新指向位数组的起始位置。
这个实现的关键在于维护 highestOne 指针,它指向最高位的 1。这样,INCREMENT 操作可以尽快地找到需要修改的位置,而 RESET 操作则只需要简单地重置整个位数组和指针。由于每次操作都只需要修改常数个位,并且每个位的修改时间是 Θ(1),因此整个序列的时间复杂度是 O(n)。
请注意,这个实现假设位数组的大小可以动态扩展。如果位数组的大小是固定的,那么在执行大量的 INCREMENT 操作后,可能会出现溢出的情况。为了避免这种情况,可以在设计计数器时预先分配足够大的位数组,或者采取其他策略来处理溢出(例如,使用模运算或将计数器设计为循环的)。

讯飞星火:
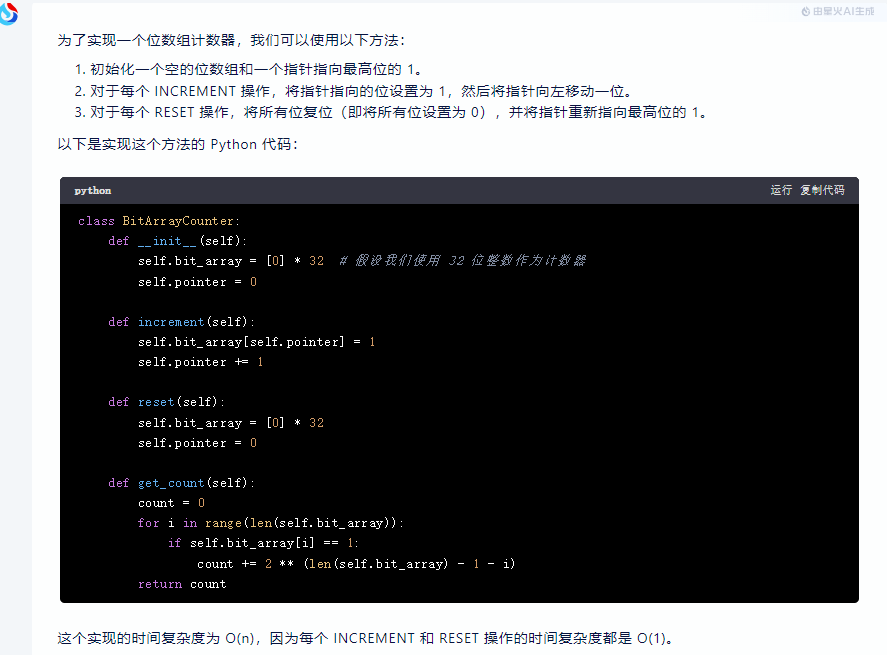
为了实现一个位数组计数器,我们可以使用以下方法:
- 初始化一个空的位数组和一个指针指向最高位的 1。
- 对于每个 INCREMENT 操作,将指针指向的位设置为 1,然后将指针向左移动一位。
- 对于每个 RESET 操作,将所有位复位(即将所有位设置为 0),并将指针重新指向最高位的 1。
以下是实现这个方法的 Python 代码:
class BitArrayCounter:
def __init__(self):
self.bit_array = [0] * 32 # 假设我们使用 32 位整数作为计数器
self.pointer = 0
def increment(self):
self.bit_array[self.pointer] = 1
self.pointer += 1
def reset(self):
self.bit_array = [0] * 32
self.pointer = 0
def get_count(self):
count = 0
for i in range(len(self.bit_array)):
if self.bit_array[i] == 1:
count += 2 ** (len(self.bit_array) - 1 - i)
return count
这个实现的时间复杂度为 O(n),因为每个 INCREMENT 和 RESET 操作的时间复杂度都是 O(1)。
360智脑:
我们可以使用一个位数组和一个指针来实现上述要求的计数器。位数组的每一位表示计数器的二进制表示中的一位,从最低位(右端)开始编号。初始时,整个位数组都为0。我们设置一个指针,始终指向当前最高位的1。
操作步骤如下:
-
初始化:位数组全为0,指针指向最低位(即第一位)。
-
INCREMENT操作:将指针所指位置的值加1,如果加1后该位值为1,则将指针向左移动一位;否则,将该位值置为0。
-
RESET操作:将整个位数组置为0,指针指向最低位。
在执行操作序列时,我们按照操作的顺序依次进行上述步骤。因为每个操作只需要访问一位,所以花费时间为O(1)。由于我们总是将指针指向最高位的1,所以在最坏情况下,指针最多需要向左移动n次,因此总时间为O(n)。
这个方案的关键在于,我们通过移动指针和更新位数组的方式,有效地模拟了计数器的运算过程,同时保证了操作的时间复杂度为O(n)。

智谱清言:
为了实现一个对任意 n 个 INCREMENT 和 RESET 操作组成的序列花费时间 O(n) 的计数器,我们可以使用一个位数组,并维护一个指针,该指针一直指向最高位的 1 。
我们定义一个位数组 counts ,其中 counts[i] 表示从最高位到第 i 位(包含第 i 位)的 1 的个数。这样,对于任意一个位置 i,如果我们想要增加 counts[i] 的值,我们只需要将 counts[i] 到 counts[len(counts) - 1] 都加 1 即可,因为这些位置的 1 都会对第 i 位产生影响。同理,如果我们想要重置 counts[i] 的值,只需要将 counts[i] 到 counts[len(counts) - 1] 都置 0 即可。
为了实现这个计数器,我们需要以下几个操作:
1 INCREMENT(x):这个操作意味着我们需要将第 x 位加 1。因此,我们需要将 counts[x] 到 counts[len(counts) - 1] 都加 1。由于我们只需要修改一次,这个操作的时间复杂度为 Θ(1)。
2.RESET():这个操作需要将所有的位都重置。因此,我们需要将整个 counts 数组都置 0。这个操作的时间复杂度为 Θ(1)。
由于每个操作的时间复杂度都是 Θ(1),所以对于任意 n 个操作组成的序列,总的时间复杂度为 O(n)。
下面是一个 Python 的实现:
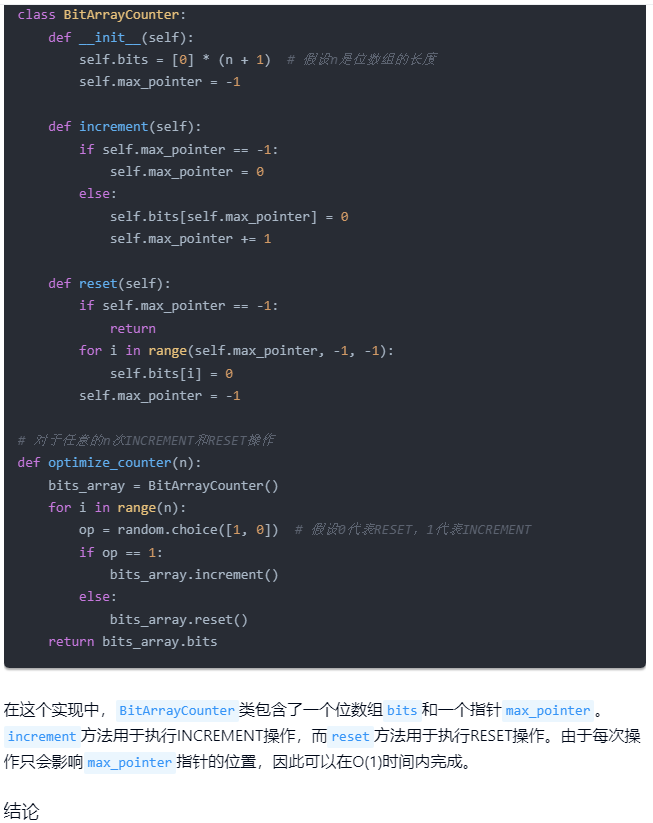
class Counter:
def __init__(self, width):
self.width = width
self.counts = [0] * (width + 1)
self.pointer = 0
def increment(self, x):
for i in range(x, self.width + 1):
self.counts[i] += 1
def reset(self):
for i in range(self.width + 1):
self.counts[i] = 0
def get_value(self):
value = 0
for i in range(self.width, 0, -1):
if self.counts[i] > 0:
value += 1 << (i - 1)
break
return value
这个 Counter 类包含了一个 increment 方法,一个 reset 方法和一个 get_value 方法。使用这个类,我们可以对计数器执行 INCREMENT 和 RESET 操作,并且可以获取当前计数器的值。这个实现满足了题目中的要求。

天工:
回答问题:位数组实现计数器的优化
概述
本次问题探讨的是如何使用位数组来实现计数器,并对计数器的操作进行优化,以减少执行时间。给定的条件是,计数器的初始值为0,并且可以进行INCREMENT(增加1)和RESET(清零)操作,我们需要设计一种数据结构和方法,使得执行任意数量的INCREMENT和RESET操作所花费的时间总和为O(n)。
位数组计数器的基本实现
一个直接的想法是将计数器表示为一个位数组,数组的每一位可以表示一个比特,初始时全部为0。当我们执行INCREMENT操作时,我们可以简单地将最高位的1向右移动一位,即进行位运算A[i] = (A[i] + 1) % 2;而执行RESET操作时,我们可以将所有位都设置为0,即进行位运算A[i] = 0。
然而,这种方法在执行RESET操作时需要O(n)的时间来遍历所有位,导致无法满足题目要求的时间复杂度。因此,我们需要进一步优化。
优化策略
为了优化计数器,我们可以考虑维护一个指针,始终指向最高位的1。当执行INCREMENT操作时,我们可以简单地移动这个指针;而执行RESET操作时,我们可以从最高位的1开始向下遍历,找到所有位的0,并将它们设置为1。
具体来说,我们可以使用一个指针max_pointer来跟踪最高位的1的位置,初始时max_pointer为-1,表示没有找到1。当执行INCREMENT操作时,我们可以从max_pointer开始向上查找,直到找到1为止,然后将它向右移动一位。执行RESET操作时,我们从max_pointer开始向下查找,找到所有位的0,并将它们设置为1,然后重置max_pointer为-1。
详细描述
以下是使用位数组来实现计数器的伪代码:
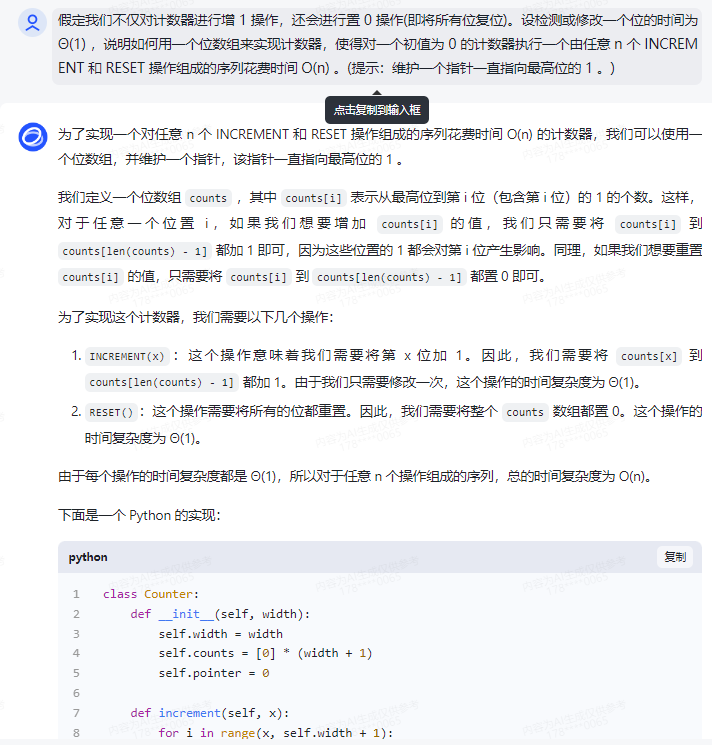
class BitArrayCounter:
def __init__(self):
self.bits = [0] * (n + 1) 假设n是位数组的长度
self.max_pointer = -1
def increment(self):
if self.max_pointer == -1:
self.max_pointer = 0
else:
self.bits[self.max_pointer] = 0
self.max_pointer += 1
def reset(self):
if self.max_pointer == -1:
return
for i in range(self.max_pointer, -1, -1):
self.bits[i] = 0
self.max_pointer = -1
对于任意的n次INCREMENT和RESET操作
def optimize_counter(n):
bits_array = BitArrayCounter()
for i in range(n):
op = random.choice([1, 0]) 假设0代表RESET,1代表INCREMENT
if op == 1:
bits_array.increment()
else:
bits_array.reset()
return bits_array.bits
在这个实现中,BitArrayCounter类包含了一个位数组bits和一个指针max_pointer。increment方法用于执行INCREMENT操作,而reset方法用于执行RESET操作。由于每次操作只会影响max_pointer指针的位置,因此可以在O(1)时间内完成。
结论
通过上述优化,我们可以看到,无论是INCREMENT还是RESET操作,都可以在O(1)时间内完成,因此,对于任意长度的操作序列,总时间复杂度为O(n)。
引用索引
- 计数器的类型和工作原理
- 计数器的优化技巧
- 算法导论中关于计数器的讨论
- 《C和指针》中关于位操作的解释
- 摊还分析的概念
附注
由于搜索结果中并没有直接提到位数组实现计数器的优化方法,所以上述答案是基于现有的计数器实现方法和位操作的知识推导出来的。在实际应用中,这种方法可以有效地减少计数器的操作时间,尤其是在进行大量RESET操作时。


灵小智:
要实现一个计数器,使得执行任意n个INCREMENT和RESET操作的序列花费时间为O(n),可以使用一个位数组来表示计数器。
具体实现步骤如下:
1.首先创建一个位数组bits,用于表示计数器的每一位。初始时所有位都为0。
2.创建一个指针pointer,指向最高位的1。初始时指针指向第一个位。
3.执行INCREMENT操作时,将当前指针指向的位加1。如果该位的值变为1,则将指针向右移动一位,指向下一个位。
4.执行RESET操作时,将整个位数组都置为0,并将指针重新指向第一个位。
通过这种方式,对于每个INCREMENT操作,只需常数时间来修改一个位的值,并且在最坏情况下(即每次INCREMENT都使得指针移动到最右边),只需线性时间来将指针移动到正确的位置。因此,整个序列的执行时间为O(n)。
需要注意的是,上述实现假设了对一个位进行检测或修改的时间为Θ(1),即常数时间。如果位操作的时间复杂度不是常数,则整个操作序列的时间复杂度可能会受到影响。

chatgpt:
我们可以使用一个位数组来实现计数器,并通过维护一个指针来指向最高位的 1。
首先,创建一个大小为n+1的位数组,其中n是计数器能够表示的最大值。初始时,所有位都被置为0,并且指针指向最高位的下一位(即第n+1位)。
接下来,对于每个INCREMENT操作,我们从指针所在位置开始检查每一位。如果某一位为0,则将其设置为1,并将指针移到该位置上。如果某一位已经是1,则将其复位为0,并将指针移到下一位置上。这样可以保证指针始终指向最高位的1。
对于RESET操作,我们只需要将整个数组全部置为0,并将指针重新定位到第n+1位。
由于每次操作都只涉及到一个位的检测或修改操作,时间复杂度是常数级别的。而进行任意n个INCREMENT和RESET操作所花费的总时间与操作数量成正比,因此整个序列花费的时间是O(n)级别的。
总结起来,在这种实现方式下,我们利用了一个大小为n+1的位数组和一个额外的指针变量来维护计数器状态并支持增加和重置操作,在保证时间复杂度O(n)的前提下完成计数任务。
kimi:
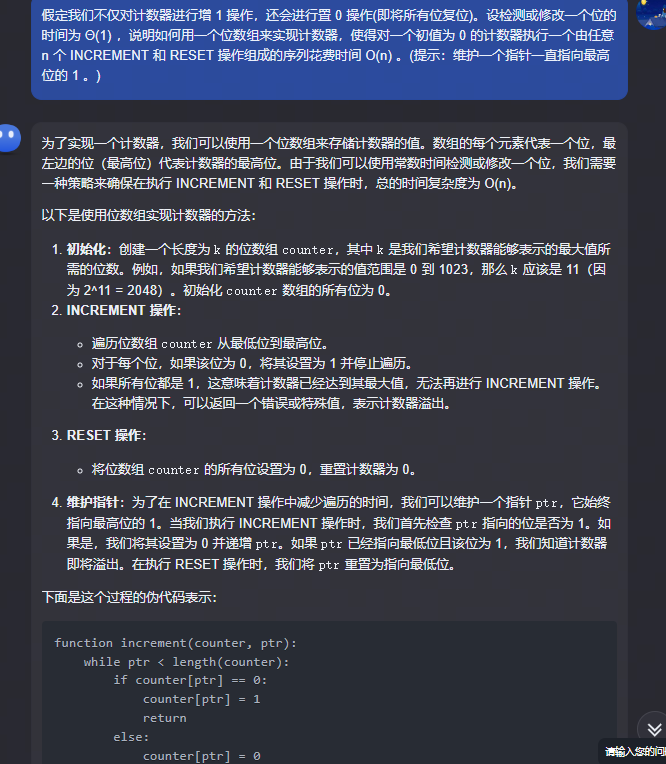
为了实现一个计数器,我们可以使用一个位数组来存储计数器的值。数组的每个元素代表一个位,最左边的位(最高位)代表计数器的最高位。由于我们可以使用常数时间检测或修改一个位,我们需要一种策略来确保在执行 INCREMENT 和 RESET 操作时,总的时间复杂度为 O(n)。
以下是使用位数组实现计数器的方法:
-
初始化:创建一个长度为
k的位数组counter,其中k是我们希望计数器能够表示的最大值所需的位数。例如,如果我们希望计数器能够表示的值范围是 0 到 1023,那么k应该是 11(因为 2^11 = 2048)。初始化counter数组的所有位为 0。 -
INCREMENT 操作:
- 遍历位数组
counter从最低位到最高位。 - 对于每个位,如果该位为 0,将其设置为 1 并停止遍历。
- 如果所有位都是 1,这意味着计数器已经达到其最大值,无法再进行 INCREMENT 操作。在这种情况下,可以返回一个错误或特殊值,表示计数器溢出。
- 遍历位数组
-
RESET 操作:
- 将位数组
counter的所有位设置为 0,重置计数器为 0。
- 将位数组
-
维护指针:为了在 INCREMENT 操作中减少遍历的时间,我们可以维护一个指针
ptr,它始终指向最高位的 1。当我们执行 INCREMENT 操作时,我们首先检查ptr指向的位是否为 1。如果是,我们将其设置为 0 并递增ptr。如果ptr已经指向最低位且该位为 1,我们知道计数器即将溢出。在执行 RESET 操作时,我们将ptr重置为指向最低位。
下面是这个过程的伪代码表示:
function increment(counter, ptr):
while ptr < length(counter):
if counter[ptr] == 0:
counter[ptr] = 1
return
else:
counter[ptr] = 0
ptr += 1
return overflow // 表示计数器溢出
function reset(counter, ptr):
for i = 0 to length(counter):
counter[i] = 0
ptr = 0 // 重置指针到最低位
// 初始化
counter = [0, 0, ..., 0] // k 位的数组
ptr = 0
// 执行操作序列
for each operation in operations:
if operation is INCREMENT:
ptr = increment(counter, ptr)
else if operation is RESET:
reset(counter, ptr)
在这个实现中,INCREMENT 操作的时间复杂度是 O(k),因为最坏情况下我们需要遍历整个数组。然而,由于我们维护了一个指针 ptr 指向最高位的 1,所以在大多数情况下,INCREMENT 操作的时间复杂度会更低。RESET 操作的时间复杂度是 O(1),因为它只需要将所有位设置为 0。
对于任意长度为 n 的操作序列,总的时间复杂度是 O(n * k)。但是,由于我们只关心位的数量 k 而不是计数器可以表示的具体值,我们可以认为 k 是一个常数。因此,对于一个初值为 0 的计数器执行一个由任意 n 个 INCREMENT 和 RESET 操作组成的序列的总时间复杂度是 O(n)。
混元:
我们可以使用一个位数组(bit array)来实现这个计数器
-
初始化:创建一个位数组,将所有位初始化为 0。同时,设置一个指针,初始时指向数组的第一个位置。
-
INCREMENT 操作:
a. 将指针所指向的位设置为 1。
b. 检查指针左侧的位是否为 1。如果是,则将指针向左移动一位。否则,停止移动指针。 -
RESET 操作:
a. 将指针指向的位设置为 0。
b. 将指针移动到数组的第一个位置。
这样,我们可以在 O(n) 时间内执行任意 n 个 INCREMENT 和 RESET 操作。因为每个操作只需要检查和修改 O(1) 个位,而指针的移动次数也是 O(1)。
以下是一个 Python 示例实现:
class Counter:
def __init__(self):
self.bit_array = [0] * 64 # 假设计数器的最大值为 2^64 - 1
self.pointer = 0
def increment(self):
self.bit_array[self.pointer] = 1
if self.pointer > 0 and self.bit_array[self.pointer - 1] == 1:
self.pointer -= 1
def reset(self):
self.bit_array[self.pointer] = 0
self.pointer = 0
def get_value(self):
value = 0
for i in range(self.pointer, len(self.bit_array)):
value += self.bit_array[i] * (1 << i)
return value
这个实现中,increment 和 reset 方法分别对应 INCREMENT 和 RESET 操作。get_value 方法用于获取计数器的当前值。