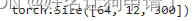在Python中，我们通常使用pandas库来处理和分析数据。数据填充是数据预处理的一个重要步骤，用于处理数据中的缺失值。以下是使用pandas库进行数据填充的示例代码：

在数据分析中，处理缺失值（空值）是一个重要的预处理步骤。缺失值的存在可能导致数据分析结果不准确或产生误导。因此，需要采取适当的策略来填补这些缺失值。以下是几种常见的空值填补办法：

1. 常数填充

将缺失值替换为某个常数，例如0、中位数、均值或者一个特殊的标识值。这种方法的优点是简单快速，但缺点是可能引入偏差，因为填充的常数可能与实际数据分布不符。

python复制代码

df['column_name'].fillna(value=0, inplace=True)

2. 均值/中位数/众数填充

根据列的数据类型（数值型或分类型），使用列的均值、中位数或众数来填充缺失值。这种方法适用于数值型数据，可以保持数据的分布特性。

python复制代码

df['column_name'].fillna(value=df['column_name'].mean(), inplace=True)

3. 插值填充

对于时间序列数据，可以使用插值方法（如线性插值、多项式插值等）来估计缺失值。这种方法能够考虑到数据随时间的变化趋势。

python复制代码

df['column_name'].interpolate(method='linear', inplace=True)

4. 基于模型预测填充

使用机器学习模型（如回归模型、决策树、随机森林等）来预测缺失值。这种方法更加复杂，但可能更准确地估计缺失值，尤其是当缺失值与其他变量存在复杂关系时。

python复制代码

	from sklearn.impute import IterativeImputer
	imputer = IterativeImputer(max_iter=10, random_state=0)
	df_filled = imputer.fit_transform(df)

5. 热卡填充（Hot Deck Imputation）

从数据集中随机选择一个非缺失值来替换缺失值。这种方法可以保持数据的分布特性，但可能引入随机性。

6. 多重插补（Multiple Imputation）

创建多个数据集，每个数据集对缺失值进行不同的填充，然后对这些数据集的分析结果进行合并，以考虑由填充缺失值引起的不确定性。

7. 基于相似性的填充

对于分类数据，可以根据其他相似样本的值来填充缺失值。例如，可以使用K近邻算法来找到与缺失值样本最相似的样本，并用这些样本的值来填充缺失值。

注意事项：

• 在选择填充方法时，应考虑数据的性质、缺失值的比例以及分析的目的。
• 在填充缺失值后，建议检查数据的分布和统计特性，以确保填充没有引入不合理的偏差。
• 有时，缺失值可能包含有用的信息（例如，某些缺失值可能表示“不适用”或“未知”），在这种情况下，应谨慎处理，避免不必要的填充。

首先，确保你已经安装了pandas库。如果没有，你可以使用pip来安装：

bash复制代码

pip install pandas

数据例样

x1	x2	x3	x4	x5	x6	x7	x8	x9	x10	x11	x12	x13	x14	y
1	22.08	11.46	2	4	4	1.585	0	0	0	1	2	100	1213	0
0	22.67	7	2	8	4	0.165	0	0	0	0	2	160	1	0
0	29.58	1.75	1	4	4	1.25	0	0	0	1	2	280	1	0
0	21.67		1	5	3	0	1	1	11	1	2	0	1	1
1	20.17	8.17	2	6	4	1.96	1	1	14	0	2	60	159	1
0		0.585	2	8	8		1	1	2	0	2		1	1
1	17.42	6.5	2	3	4	0.125	0	0	0	0	2	60	101	0
0	58.67	4.46	2	11	8	3.04	1	1	6	0	2	43	561	1
1	27.83	1	1	2	8	3	0	0	0	0	2	176	538	0
0	55.75	7.08	2	4	8	6.75	1	1	3	1	2	100	51	0
1	33.5	1.75	2	14	8		1	1	4	1	2	253	858	1
1	41.42	5	2	11	8	5	1	1	6	1	2	470	1	1
1	20.67	1.25	1	8	8	1.375	1	1	3	1	2	140		0
	34.92	5	2	14	8	7.5	1	1	6	1	2	0	1001	1
1		2.71	2	8	4	2.415	0	0		1	2	320	1	0
1	48.08	6.04	2	4	4		0	0	0	0	2	0	2691	1
1	29.58	4.5	2	9	4	7.5	1	1	2	1	2	330	1	1
0	18.92	9	2	6	4	0.75	1	1	2	0	2	88	592	1
1	20	1.25	1	4	4	0.125	0	0	0	0	2	140	5	0
0	22.42	5.665	2	11	4	2.585	1		7	0	2	129	3258	1
0	28.17	0.585	2	6	4	0.04		0	0	0	2		1005	0
0	19.17	0.585	1	6	4	0.585	1	0	0	1	2	160	1	0
1	41.17	1.335	2	2	4	0.165	0	0	0	0	2	168	1	0
1	41.58	1.75	2	4	4	0.21	1	0		0	2	160	1	0
	19.5		2	6	4	0.79	0	0	0	0	2	80	351	0
1	32.75	1.5	2	13	8	5.5	1	1	3	1	2	0	1	1
1	22.5	0.125	1	4	4	0.125	0	0	0	0	2	200	71	0
1	33.17	3.04	1	8	8	2.04	1	1	1	1	2	180	18028	1
0	30.67	12	2	8	4	2	1	1	1	0	2	220	20	1
1	23.08	2.5	2	8	4	1.085	1	1	11	1	2	60	2185	1
1	27	0.75	2	8	8		1	1	3	1	2	312	151	1
0	20.42	10.5	1	14	8	0	0	0	0	1	2	154	33	0
1	52.33	1.375	1	8	8	9.46	1	0		1	2	200	101	0
1	23.08	11.5	2	9	8	2.125	1	1	11	1	2	290	285	1
1	42.83	1.25	2	7	4	13.875	0	1	1	1	2	352	113	0
1	74.83	19	1	1	1	0.04	0	1	2	0	2	0	352	0
1	25		2	6	4	3	1	0	0	1		20	1	1
1	39.58	13.915	2	9	4	8.625	1	1	6	1	2	70	1	1
0	47.75	8	2	8	4	7.875	1	1	6	1	2	0	1261	1
0	47.42	3	2	14	4	13.875	1	1	2	1	2	519	1705	1
1	23.17	0	2	13	4	0.085	1	0		0	2	0	1	1
1	22.58	1.5	1	6	4	0.54	0	0	0	1	2	120	68	0
1	26.75	1.125	2	14	8	1.25	1	0	0	0	2	0	5299	1
1	63.33	0.54	2	8	4	0.585	1	1	3	1	2	180	1	0
1	23.75	0.415	1	8	4	0.04	0	1	2	0	2	128	7	0
0	20.75		2	11	4	0.71	1	1	2	1	2	49	1	1
0	24.5	1.75	1	8	4	0.165	0	0	0	0	2	132	1	0
1	16.17	0.04	2	8	4	0.04	0	0	0	0	2	0	1	1
0	29.5	2	1	10	8	2	0	0	0	0	2	256	18	0
0	52.83	15	2	8	4	5.5	1	1	14	0	2	0	2201	1
1	32.33	3.5	2	4	4	0.5	0	0	0	1	2	232	1	0
1	21.08	4.125	1	3	8	0.04	0	0	0		2	140	101	0
1	28.17	0.125	1	4	4	0.085	0	0	0	0	2	216	2101	0
1	19	1.75	1	8	4	2.335	0	0	0	1	2	112	7	0
1	27.58	3.25		11	8	5.085	0	1	2	1	2		2	0
1	27.83	1.5	2	9	4	2	1	1	11	1	2	434	36	1
1		6.5	2	6	5	3.5	1	1	1	0	2	0	501	1
0	37.33	2.5	2	3	8	0.21	0	0	0	0	2	260		0
1	42.5	4.915	1	9	4	3.165	1		0	1	2	52	1443	1
1	56.75	12.25	2	7	4	1.25	1	1	4	1	2	200	1	1
1	43.17	5	2	3	5	2.25	0	0	0	1	2	141	1	0
0	23.75	0.71	2	9	4	0.25	0	1	1	1	2	240	5	0
1	18.5	2	2	3	4	1.5	1	1	2	0	2	120	301	1
0	40.83	3.5	2	3	5	0.5	0	0	0	0	1	1160	1	0
0	24.5	0.5	2	11	8	1.5	1	0	0	0	2	280	825	1
1	42	9.79	2	14	8	7.96	1	1	8	0	2	0	1	1
0	19.5	0.165	2	11	4	0.04	0	0	0	1	2	380	1	0
1	21.5	11.5	2	3	4	0.5	1	0	0	1	2	100	69	0
1	31.25	2.835	2	1	1	0	0	1	5	0	2	176	147	0
	27.25	1.585	2	13	8	1.835	1	1	12	1	2	583	714	1
1	48.75	26.335	1	1	1	0	1	0	0	1	2	0	1	0
0	30.42	1.375	2	9	8	0.04	0	1	3	0	2	0	34	0
1	29.42	1.25	2	9	4	1.75	0	0		0	2		1	0
1		5.04	1		5	1.5	1	1	8	1	2	144	8	1
1	40.25	21.5	2	10	9	20	1	1	11	0	2	0	1201	1
1	36.5	4.25	2	11	4	3.5	0	0	0	0	2	454	51	0
1	25.58	0.335	2	4	8	3.5	0	0	0	1	2	340	1	0
1	29.83	3.5	2	8	4	0.165	0	0	0	0	2	216	1	0
1	23.08	0	2	4	4	1	0	1	11	0	1	0	1	0
0	32.17	1.46	2	9	4	1.085	1	1	16	0	2	120	2080	1
1	25.17	3.5	2	13	4	0.625	1	1	7	0	2	0	7060	1
0	35.17	3.75	2	1	1	0	0	1	6	0	2	0	201	0
0	18.58	10	2	2	4	0.415	0	0	0	0	2	80	43	0
1	39.92	5	2	3	5	0.21	0	0	0	0	2	550	1	0
1	23.42	1	2	8	4	0.5	0	0	0	1	1	280	1	0
1	37.58	0	2	8	4	0	0	0	0	0	3	184	1	1
0	24.75	13.665	2	11	8	1.5	0	0	0	0	2	280	2	0
0	47	13	2	3	5	5.165	1	1	9	1	2	0	1	1
1	34.17	5.25	2	9	4	0.085	0	0	0	1	2	290	7	1
1	22.17	0.585	1	1	1	0	0	0	0	0	2	100	1	0
1	27.75	1.29	2	4	8	0.25	0	0	0	1	1	140	1	0
1	42.75	4.085	2	6	4	0.04	0	0	0	0	2	108	101	0
1	28.67	14.5	2	2	4	0.125	0	0	0	0	2	0	287	0
1	36.25	5	2	8	5	2.5	1	1	6	0	2	0	368	1
0	18.17	10	1	11	8	0.165	0	0	0	0	2	340	1	0
1	21.25	1.5	2	9	4	1.5	0	0	0	0	2	150	9	1
0	38.92	1.665	2	6	4	0.25	0	0	0	0	2	0	391	0
1	31.83	0.04	1	7	4	0.04	0	0	0	0	2	0	1	0
0	17.33	9.5	2	6	4	1.75	0	1	10	1	2	0	11	0
0	20.42	0.835	2	11	4	1.585	1	1	1	0	2	0	1	1
0	39.08	4	2	8	4	3	0	0	0	0	2	480	1	0
1	38.67	0.21	2	4	4	0.085	1	0	0	1	2	280	1	1
1	27.67	13.75	2	9	4	5.75	1	0	0	1	2	487	501	1
1	27.75	0.585	1	13	4	0.25	1	1	2	0	2	260	501	1
1	19	0	1	1	1	0	0	1	4	0	2	45	2	0
0	25	0.875	2	14	8	1.04	1	0	0	1	2	160	5861	1
1	27.67	2	2	14	8	1	1	1	4	0	2	140	7545	1
1	22.25	9	2	6	4	0.085	0	0	0	0	2	0	1	0
0	49.83	13.585	2	4	8	8.5	1	0	0	1	2	0	1	1
1	32.33	2.5	2	8	4	1.25	0	0	0	1	2	280	1	0
1	38.25	10.125	1	4	4	0.125	0	0	0	0	2	160	1	0
1	47.33	6.5	2	8	4	1	0	0	0	1	2	0	229	0
1	27.83	4	1	3	8	5.75	1	1	2	1	2	75	1	0
0	35.75	0.915	2	6	4	0.75	1	1	4	0	2	0	1584	1
1	33.58	0.25	2	3	5	4	0	0	0	1	1	420	1	0
1	34.08	0.08	1	7	5	0.04	1	1	1	1	2	280	2001	1
0	20.75	10.335	2	13	8	0.335	1	1	1	1	2	80	51	1
1	33.17	1	2	14	4	0.75	1	1	7	1	2	340	4072	1
1	22.75	11	2	11	4	2.5	1	1	7	1	2	100	810	1
1	48.75	8.5	2	8	8	12.5	1	1	9	0	2	181	1656	1
1	40.58	5	2	8	4	5	1	1	7	0	2	0	3066	1
1	20.67	0.835	1	8	4	2	0	0	0	1	1	240	1	0
0	38.75	1.5	2	1	1	0	0	0	0	0	2	76	1	0
0	57.08	19.5	2	8	4	5.5	1	1	7	0	2	0	3001	1
0	31.25	3.75	2	13	8	0.625	1	1	9	1	2	181	1	1
1	22	0.79	2	9	4	0.29	0	1	1	0	2	420	284	0
0	58.33	10	2	11	4	4	1	1	14	0	2	0	1603	1
1	28.92	0.375	2	8	4	0.29	0	0	0	0	2	220	141	0
0	46	4	2	5	3	0	1	0	0	0	2	100	961	1
1	21	3	1	2	4	1.085	1	1	8	1	2	160	2	1
0	24.75	12.5	2	6	4	1.5	1	1	12	1	2	120	568	1
0	20.83	0.5	1	10	2	1	0	0	0	0	2	260	1	0
1	24.58	13.5	1	1	1	0	0	0	0	0	2	184	1	0
0	26.5	2.71	1	8	4	0.085	0	0	0	0	1	80	1	0
1	40.92	0.835	2	1	1	0	1	0	0	0	2	130	2	0
0	38.33	4.415	2	8	4	0.125	0	0	0	0	2	160	1	0
1	19.58	0.585	2	1	1	0	0	1	3	0	2	350	770	0
1	39.25	9.5	2	7	4	6.5	1	1	14	0	2	240	4608	1
1	25.75	0.5	2	8	4	1.46	1	1	5	1	2	312	1	1
0	46.08	3	2	8	4	2.375	1	1	8	1	2	396	4160	1
1	19.67	10	1	4	8	0.835	1	0	0	1	2	140	1	0
0	22.25	1.25	1	1	1	3.25	0	0	0	0	2	280	1	0
1	18.83	3.54	1	1	1	0	0	0	0	1	2	180	2	0
1	64.08	20	2	14	8	17.5	1	1	9	1	2	0	1001	1
0	16.5	1.25	2	11	4	0.25	0	1	1	0	2	108	99	0
0	68.67	15	2	10	9	0	1	1	14	0	2	0	3377	1
1	76.75	22.29	2	10	9	12.75	1	1	1	1	2	0	110	1
0	15.92	2.875	2	11	4	0.085	0	0	0	0	2	120	1	0
1	34.83	4	2	2	5	12.5	1	0	0	1	2	184	1	0
0	47.42	8	2	10	5	6.5	1	1	6	0	2	375	51101	1
1	23.17	0	2	8	4	0	0	0	0	0	3	184	1	1
1	45.17	1.5	2	8	4	2.5	1	0	0	1	2	140	1	0
1	15.17	7	2	10	4	1	0	0	0	0	2	600	1	0
1	18.83	0.415	1	8	4	0.165	0	1	1	0	2	200	2	0
1	52.5	6.5	2	4	4	6.29	1	1	15	0	2	0	11203	1
1	19.17	0	1	7	5	0	0	0	0	1	1	500	2	1
1	18	0.165	2	11	7	0.21	0	0	0	0	2	200	41	1
1	37.5	0.835	2	10	4	0.04	0	0	0	0	2	120	6	0
1	22.67	1.585	1	9	4	3.085	1	1	6	0	2	80	1	1
1	47.83	4.165	2	14	5	0.085	0	0	0	1	2	520	1	0
1	34.08	2.5	2	8	4	1	0	0	0	0	2	460	17	0
0	33.08	1.625	2	2	4	0.54	0	0	0	1	2	0	1	0
1	43.08	0.375	1	8	4	0.375	1	1	8	1	2	300	163	1
1	34.5	4.04	1	3	5	8.5	1	1	7	1	2	195	1	1
1	42.75	3	2	3	5	1	1	0	0	0	2	0	201	0
1	18.25	0.165	2	2	4	0.25	0	0	0	1	1	280	1	0
1	23.08	2.5	2	1	1	0.085	0	0	0	1	2	100	4209	0
0	22.5	8.46	1	14	4	2.46	0	0	0	0	2	164	1	1
1	17.92	0.205	2	6	4	0.04	0	0	0	0	2	280	751	0
1	18.42	10.415	1	6	4	0.125	1	0	0	0	2	120	376	0
0	27.67	1.5	2	7	4	2	1	0	0	0	1	368	1	0
0	18.92	9.25	1	8	4	1	1	1	4	1	2	80	501	1
1	22.67	0.75	2	3	4	1.585	0	1	1	1	2	400	10	0
1	62.5	12.75	1	8	8	5	1	0	0	0	2	112	1	0
0	23.5	9	2	11	4	8.5	1	1	5	1	2	120	1	1
1	35.25	3.165	2	14	8	3.75	1	0	0	1	2	680	1	0
0	56.83	4.25	1	1	1	5	0	0	0	1	2	0	5	0
0	53.33	0.165	2	1	1	0	0	0	0	1	1	62	28	0
1	41.17	4.04	2	13	8	7	1	1	8	0	2	320	1	1
1	42.17	5.04	2	11	8	12.75	1	0	0	1	2	92	1	1
1	41.17	1.25	1	9	4	0.25	0	0	0	0	2	0	196	0
0	33.75	0.75	2	4	5	1	1	1	3	1	2	212	1	0
1	25.67	12.5	2	13	4	1.21	1	1	67	1	2	140	259	1
1	24.33	6.625	1	2	4	5.5	1	0	0	1	1	100	1	1
1	23.33	11.625	1	9	4	0.835	1	0	0	1	2	160	301	1
1	30.67	2.5	2	13	8	2.25	0	0	0	1	1	340	1	0
1	37.17	4	2	8	5	5	1	0	0	1	1	280	1	0
1	26.25	1.54	2	9	4	0.125	0	0	0	0	2	100	1	0
0	29.75	0.665	2	9	4	0.25	0	0	0	1	2	300	1	0
0	23	1.835	2	5	3	0	0	1	1	0	2	200	54	0
1	17.25	3	2	4	4	0.04	0	0	0	1	2	160	41	0
1	29.25	14.79	2	6	4	5.04	1	1	5	1	2	168	1	1
0	28.58	3.54	2	3	5	0.5	1	0	0	1	2	171	1	0
1	34.58	0	2	8	4	0	0	0	0	0	3	184	1	0
1	23.42	0.585	2	8	8	0.085	1	0	0	0	2	180	1	0
1	25	11.25	2	8	4	2.5	1	1	17	0	2	200	1209	1
0	18.75	7.5	2	11	4	2.71	1	1	5	0	2	184	26727	1
1	17.08		2	11	4	0.335	0	1	4	0	2	160	9	0
0	16.08	0.335	2	1	1	0	0	1	1	0	2	160	127	0
1	32.92	2.5	2	6	4	1.75	0	1	2	1	2	720	1	0
0	20.33	10	2	8	8	1	1	1	4	0	2	50	1466	1
0		1.75	1	5	3	0	0	0	0	0	2	160	1	0
1	33.17	1.04	2	12	8	6.5	1	0	0	1	2	164	31286	1
0	25.33	2.085	2	8	8	2.75	1	0	0	1	2	360	2	0
0	24.75	3	2	11	8	1.835	1	1	19	0	2	0	501	1
1	30.83	0	2	9	4	1.25		1	1	0		202	1	1
1	20.75	5.085	1	5	4	0.29	0	0	0	0	2	140	185	0
0	40.33	8.125	1	4	4	0.165	0	1	2	0	2	184	19	0
1	29.42	1.25	2	8	8	0.25	0	1	2	1	2	400	109	0
1	40.92	0.5	1	7	4	0.5	0	0	0	1	2	130	1	0
0	29.5	0.46	2	4	4	0.54	1	1	4	0	2		501	1
1	54.42	0.5	1	4	8	3.96	1	0	0	0	2	180	315	1
1	34	5.5	1	8	4	1.5	0	0	0	1	2	60	1	0
1	25	12	2	4	4	2.25	1	1	2	1	2	120	6	0
0	26.58	2.54	1	1	1	0	0	0	0	1	2	180	61	0
0	33.08	4.625	2	11	8		1	1	2	0	2	0	1	1
1	33.67	2.165	2	8	4	1.5	0	0	0	0	3	120	1	0
1	36.17		2	3	5	5	0	0	0	0	2	210	688	0
1	19.5	0.29	2	4	4	0.29	0	0	0	0	2	280	365	0
1	24.17	0.875	2	11	4	4.625	1	1	2	1	2	520	2001	1
0	30.5	6.5	2	8	5	4	1	1	7	1	2	0	3066	1
1	20	7	2	8	4	0.5	0	0	0	0	2	0	1	0
1	25.33	0.58	2	8	4	0.29	1	1	7	1	2	96	5125	1
1	29.58	4.75	2	7	4	2	0	1	1	1	2	460	69	0
1	43.17	2.25	2	3	5	0.75	1	0	0	0	2	560	1	0
1	28.75	1.165	2	4	4	0.5	1	0	0	0	1	280	1	0
1	31.57	3	1	3	5	7	0	0	0	0	2	0	2	0
1	20.25	9.96	2	10	2	0	1	0	0	0	2	0	1	1
1	45	8.5	2	13	8	14	1	1	1	1	2	88	2001	1
0	22.83	2.29	2	11	8	2.29	1	1	7	1	2	140	2385	1
0	20.67	3	2	11	4	0.165	1	1	3	0	2	100	7	1
1	27.83	1.5	2	9	4	2.25	0	1	1	1	2	100	4	0
1	40.92	2.25	1	14	8	10	1	0	0	1	2	176	1	0
1	56.42	28	1	8	4	28.5	1	1	40	0	2	0	16	1
0	64.08	0.165	2	1	1	0	1	1	1	0	2	232	101	1
0	22.42	11.25	1	14	8	0.75	1	1	4	0	2	0	322	1
0	24.33	2.5	1	3	5	4.5	0	0	0	0	2	200	457	0
0	69.5	6	2	1	1	0	0	0	0	0	1	0	1	0
1	35.58	0.75	2	4	4	1.5	0	0	0	1	2	231	1	0
1	48.33	12	2	7	4	16	1	0	0	0	1	110	1	1
0	28.08	15	1	10	9	0	1	0	0	0	2	0	13213	1
1	35.17	2.5	2	4	4	4.5	1	1	7	0	2	150	1271	1
1	49.5	7.585	2	3	5	7.585	1	1	15	1	2	0	5001	1
1	80.25	5.5	2	8	4	0.54	1	0	0	0	2	0	341	0
1	29.25	13	2	2	8	0.5	0	0	0	0	2	228	1	0
0	16.92	0.5	2	3	4	0.165	0	1	6	1	2	240	36	0
0	16	0.165	2	6	4	1	0	1	2	1	2	320	2	0
1	60.08	14.5	2	1	1	18	1	1	15	1	2	0	1001	1
1		2	2	4	8		1	1	2	1	2	181	1	1
1	41.5	1.54	2	3	5	3.5	0	0	0	0	2		1	1
1	24.08	9	2	6	4	0.25	0	0	0	1	2	0	1	0
1	24.5	13.335	1	6	4		0	0	0	1	2	120	476	0
1	34.75	15	2	12	7	5.375	1	1	9	1	2	0	135	1
1	33.67	1.25	2	9	4	1.165	0	0	0	0	2	120	1	0
0	40.83	10		11	8	1.75	1	0	0	0	2	29	838	1
1	20.42	1.835	2	8	4	2.25	1	1	1	0	2	100	151	1
1	37.5	1.125	1	2	4	1.5	0	0	0	1	2	431	1	1
1	48.5	4.25	2	7	4	0.125	1	0	0	1	2	225	1	1
1	23	0.75	2	7	4	0.5	0	0	0	1	1	320	1	0
1		3.375	2	8	8	8.29	0	0	0	1	2	0	1	0
1	16.33	2.75	2	6	4	0.665	0	1	1	0	2	80	22	0
	22.67		2	11	8	1.335	1	0	0	0		100	1	1
0	21.75	11.75	2	8	4	0.25	0	0	0	1	2	180	1	0
0	25.08	2.54	1	6	4	0.25	1	0	0	1	2	370	1	1
1	36.33	2.125	1	9	4	0.085	1	1	1	0	2	50	1188	1
0	28.58	3.75	2	8	4	0.25	0	1	1	1	2	40	155	0
1	22.17	12.125	2	8	4	3.335	0	1	2	1	2	180	174	0
1	34.17	1.54	2	13	4	1.54	1	1	1	1	2	520	50001	1
1	35	2.5	2	3	4	1	0	0	0	1	2	210	1	0
1	28.58	3.625	2	6	4	0.25	0	0	0	1	2	100	1	0
0	19.17	5.415	2	3	8	0.29	0	0	0	0	2	80	485	0
1	23.25	1	2	8	4	0.835	1	0	0	0	1	300	1	1
1	16.5	0.125	2	8	4	0.165	0	0	0	0	2	132	1	0
0	20.08	0.125	2	11	4	1	0	1	1	0	2	240	769	1
1	22.33	11	2	9	4	2	1	1	1	0	2	80	279	1
1	34	5.085	1	3	5	1.085		0	0	1	2	480	1	0
0	57.08	0.335	2	3	5	1	1	0	0	1	2	252	2198	0
1	16.25	0.835	2	7	4	0.085	1	0	0	0	1	200	1	0
1	32.83		2	13	8	2.75	1	1	6	0	2	160	2073	1
1	48.25	25.085	2	9	4	1.75	1	1	3	0	2		15	1
1	34.17	2.75	2	3	5	2.5	0	0	0	1	2	232	201	0
1	18.33	1.21	1	10	2	0	0	0	0	0	2	100	1	0
1	44.25	0.5	2	7	4	10.75	1	0	0	0	1	400	1	0
1	38.92	1.75	2	4	4	0.5	0	0	0	1	2	300	3	0
1	31.58	0.75	1	6	4	3.5	0	0	0	1	2	320	1	0
1	25.08	1.71	2	14	4	1.665	1	1	1	1	2	395	21	1
1	65.42	11	2	10	9	20	1	1	7	1	2	22	1	1
1	41.33	0	2	8	5	15	1	0	0	0	2	0	1	1
1	31.25	1.125	2	1	1	0	0	1	1	0	2	96	20	0
0	36.75	4.71	2	1	1	0	0	0	0	0	2	160	1	0
1	32.33	7.5	2	10	5	1.585	1	0	0	1	1	420	1	0
0	31.92	3.125	2	1	1	3.04	0	1	2	1	2	200	5	0
1	24.83	2.75	2	8	4	2.25	1	1	6	0	2	184	601	1
1	21.92	0.54	1	14	4	0.04	1	1	1	1	2	840	60	1
1	34.25	3	2	13	8	7.415	1	0	0	1	2	0	1	1
1	51.83	3	1	1	1	1.5	0	0	0	0	2	180	5	0
0	31.57	1.5	2	1	1	0	0	1	2	1	2	200	106	0
1	38.42	0.705	2	8	4	0.375	0	1	2	0	2	225	501	0
1	39.17	1.71	2	14	4	0.125	1	1	5	1	2	480	1	1
1	18.17	2.46	2	8	7	0.96	0	1	2	1	2	160	588	0
1	39	5	2	13	4	3.5	1	1	10	1	2	0	1	1
1	20	11.045	2	8	4	2	0	0	0	1	2	136	1	0
1	32.75	2.335	2	2	8	5.75	0	0	0	1	2	292	1	0
1	18.58	5.71	2	2	4	0.54	0	0	0	0	2	120	1	0
0	15.83	7.625	2	11	4	0.125	0	1	1	1	2	0	161	0
1	39.33	5.875	2	13	8	10	1	1	14	1	2	399	1	1
0	19.58	0.665	2	9	4	1.665	0	0	0	0	2	220	6	0
1	21.33	10.5	2	8	4	3	1	0	0	1	2	0	1	1
0	22.67	0.75	2	8	4	2	0	1	2	1	2	200	395	0
1	25.67	3.25	2	8	8	2.29	0	1	1	1	2	416	22	0
1	21.08	10.085	1	10	8	1.25	0	0	0	0	2	260	1	0
0	49	1.5	2	5	3	0	1	0	0	1	2	100	28	0
1	20.67	5.29	2	11	4	0.375	1	1	1	0	2	160	1	0
0	19.67	0.21	2	11	8	0.29	1	1	11	0	2	80	100	1
1	21.83	0.25	2	2	8	0.665	1	0	0	1	2	0	1	1
1	26.83	0.54	2	4	1	0	0	0	0	0	2	100	1	0
0	38.58	5	2	13	4	13.5	1	0	0	1	2	980	1	0
0	50.08	12.54	2	6	4	2.29	1	1	3	1	2	156	1	1
0	15.75	0.375	2	8	4	1	0	0	0	0	2	120	19	0
0	24.5	12.75	2	8	5	4.75	1	1	2	0	2	73	445	1
1	21	4.79	1	9	4	2.25	1	1	1	1	2	80	301	1
1	22.08	11	2	13	4	0.665	1	0	0	0	2	100	1	1
1	54.58	9.415	2	1	1	14.415	1	1	11	1	2	30	301	1
1	18.08	5.5	2	4	4	0.5	1	0	0	0	2	80	1	1
1	36.67	4.415	1	4	4	0.25	1	1	10	1	2	320	1	1
1	38.17	10.125	2	14	4	2.5	1	1	6	0	2	520	197	1
1	21.83	1.54	2	4	4	0.085	0	0	0	1	2	356	1	0
0	51.92	6.5	2	3	5	3.085	0	0	0	1	2	73	1	0
1	22.17	2.25	2	3	4	0.125	0	0	0	0	2	160	11	0
1	52.42	1.5	2	2	4	3.75	0	0	0	1	2	0	351	0
0	60.92	5	2	6	4	4	1	1	4	0	2	0	100	1
1	20.17	5.625	2	9	4	1.71	1	0	0	0	1	120	1	1
1	23.25	4	2	8	5	0.25	1	0	0	1	2	160	1	1
1	36.17	0.42	1	9	4	0.29	0	0	0	1	2	309	3	0

 

以下是对应上述缺失值处理方法的Python代码示例：

1. 常数填充

 在这个修改后的代码中，constant_for_continuous是填充连续变量缺失值的常数（这里用0作为示例），而constant_for_discrete是填充离散变量缺失值的常数（这里用字符串'未知'作为示例）。您可以根据需要更改这些常数的值。

import pandas as pd

# 读取Excel文件
df = pd.read_excel("银行贷款审批数据.xlsx")

# 定义连续变量和离散变量列表
continuous_vars = ['x2', 'x3', 'x5', 'x6', 'x7', 'x10', 'x13', 'x14']
discrete_vars = ['x1', 'x4', 'x8', 'x9', 'x11', 'x12']

# 使用常数填充连续变量的缺失值（例如，使用常数0）
constant_for_continuous = 0
for var in continuous_vars:
    df[var].fillna(constant_for_continuous, inplace=True)

# 使用常数填充离散变量的缺失值（例如，使用字符串'未知'）
constant_for_discrete = '未知'
for var in discrete_vars:
    df[var].fillna(constant_for_discrete, inplace=True)

# 检查是否还有缺失值
missing_values = df.isnull().sum().sum()
if missing_values == 0:
    print("所有缺失值已填充。")
else:
    print("仍有缺失值未填充。")

# 输出填充后的数据框的前几行
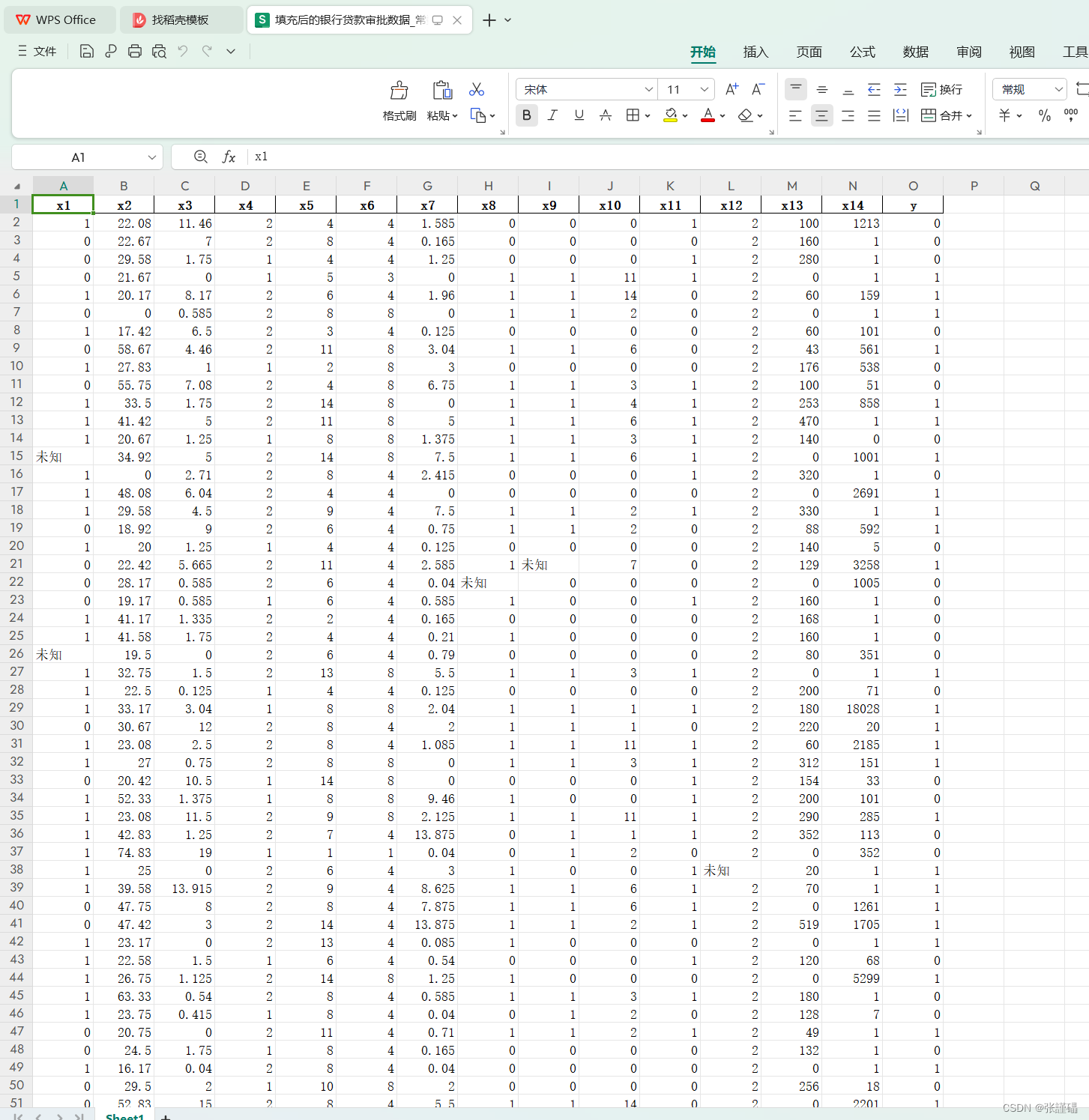
print(df.head())

# 保存填充后的数据框到Excel文件
df.to_excel("填充后的银行贷款审批数据_常数填充.xlsx", index=False)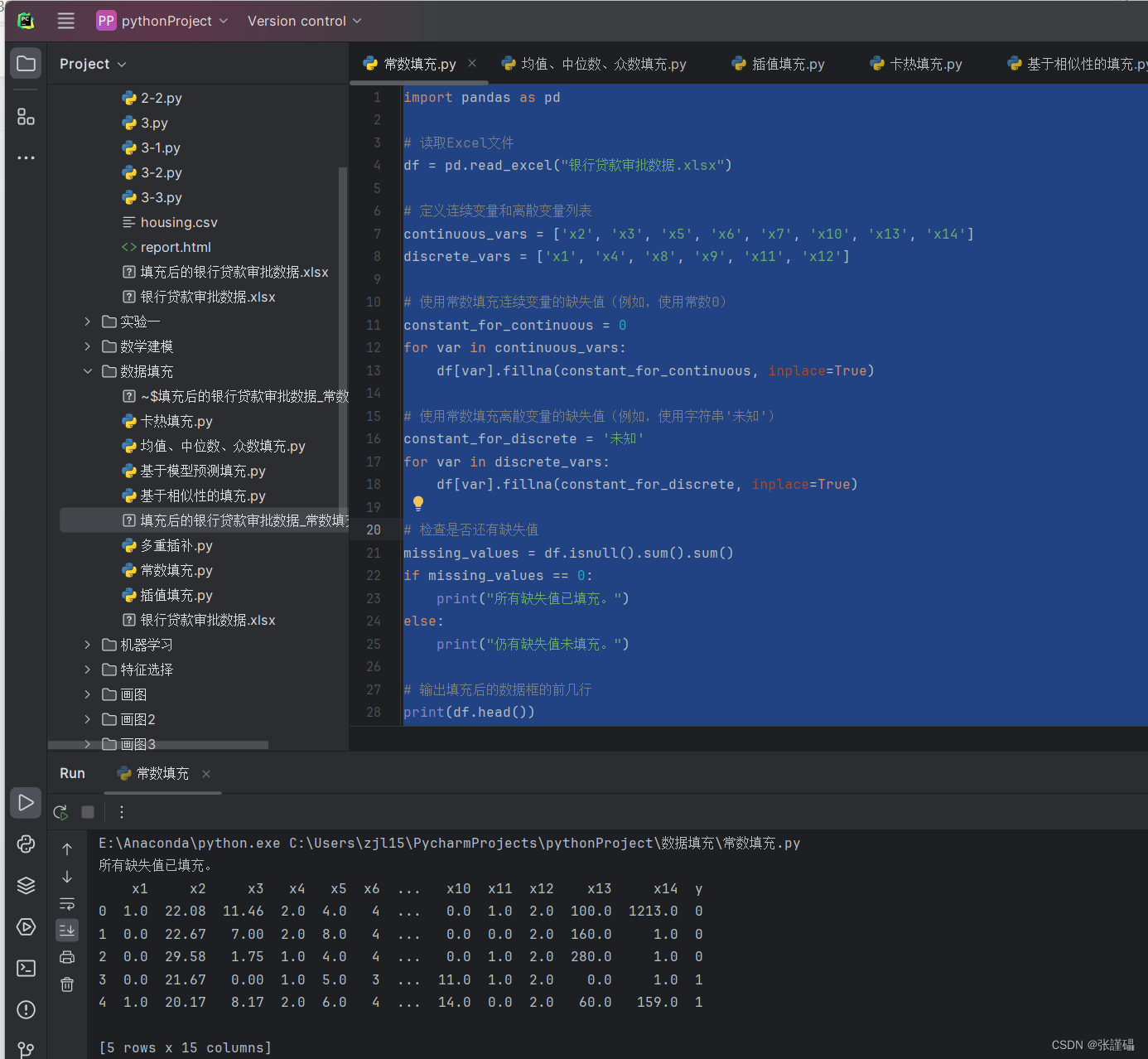

 

 

 

 

2. 均值/中位数/众数填充

import pandas as pd
from scipy import stats

# 读取Excel文件
df = pd.read_excel("银行贷款审批数据.xlsx")

# 定义连续变量和离散变量列表
continuous_vars = ['x2', 'x3', 'x5', 'x6', 'x7', 'x10', 'x13', 'x14']
discrete_vars = ['x1', 'x4', 'x8', 'x9', 'x11', 'x12']

# 使用均值填充连续变量的缺失值
for var in continuous_vars:
    df[var].fillna(df[var].mean(), inplace=True)

# 或者使用中位数填充连续变量的缺失值
# for var in continuous_vars:
#    df[var].fillna(df[var].median(), inplace=True)

# 使用众数填充离散变量的缺失值
for var in discrete_vars:
    mode_value = stats.mode(df[var].dropna())[0][0]
    df[var].fillna(mode_value, inplace=True)

# 检查是否还有缺失值
missing_values = df.isnull().sum().sum()
if missing_values == 0:
    print("所有缺失值已填充。")
else:
    print("仍有缺失值未填充。")

# 输出填充后的数据框的前几行
print(df.head())

# 保存填充后的数据框到Excel文件
df.to_excel("填充后的银行贷款审批数据_均值众数填充.xlsx", index=False)

3. 插值填充

import pandas as pd

# 读取Excel文件
df = pd.read_excel("银行贷款审批数据.xlsx")

# 定义连续变量和离散变量列表
continuous_vars = ['x2', 'x3', 'x5', 'x6', 'x7', 'x10', 'x13', 'x14']
discrete_vars = ['x1', 'x4', 'x8', 'x9', 'x11', 'x12']

# 使用线性插值填充连续变量的缺失值
for var in continuous_vars:
    df[var].interpolate(method='linear', inplace=True)

# 对于离散变量，插值通常不是合适的方法，因为它们通常是分类数据。
# 因此，我们仍然使用众数来填充离散变量的缺失值。
for var in discrete_vars:
    most_frequent_value = df[var].mode()[0]
    df[var].fillna(most_frequent_value, inplace=True)

# 检查是否还有缺失值
missing_values = df.isnull().sum().sum()
if missing_values == 0:
    print("所有缺失值已填充。")
else:
    print("仍有缺失值未填充。")

# 输出填充后的数据框的前几行
print(df.head())

# 保存填充后的数据框到Excel文件
df.to_excel("填充后的银行贷款审批数据_插值填充.xlsx", index=False)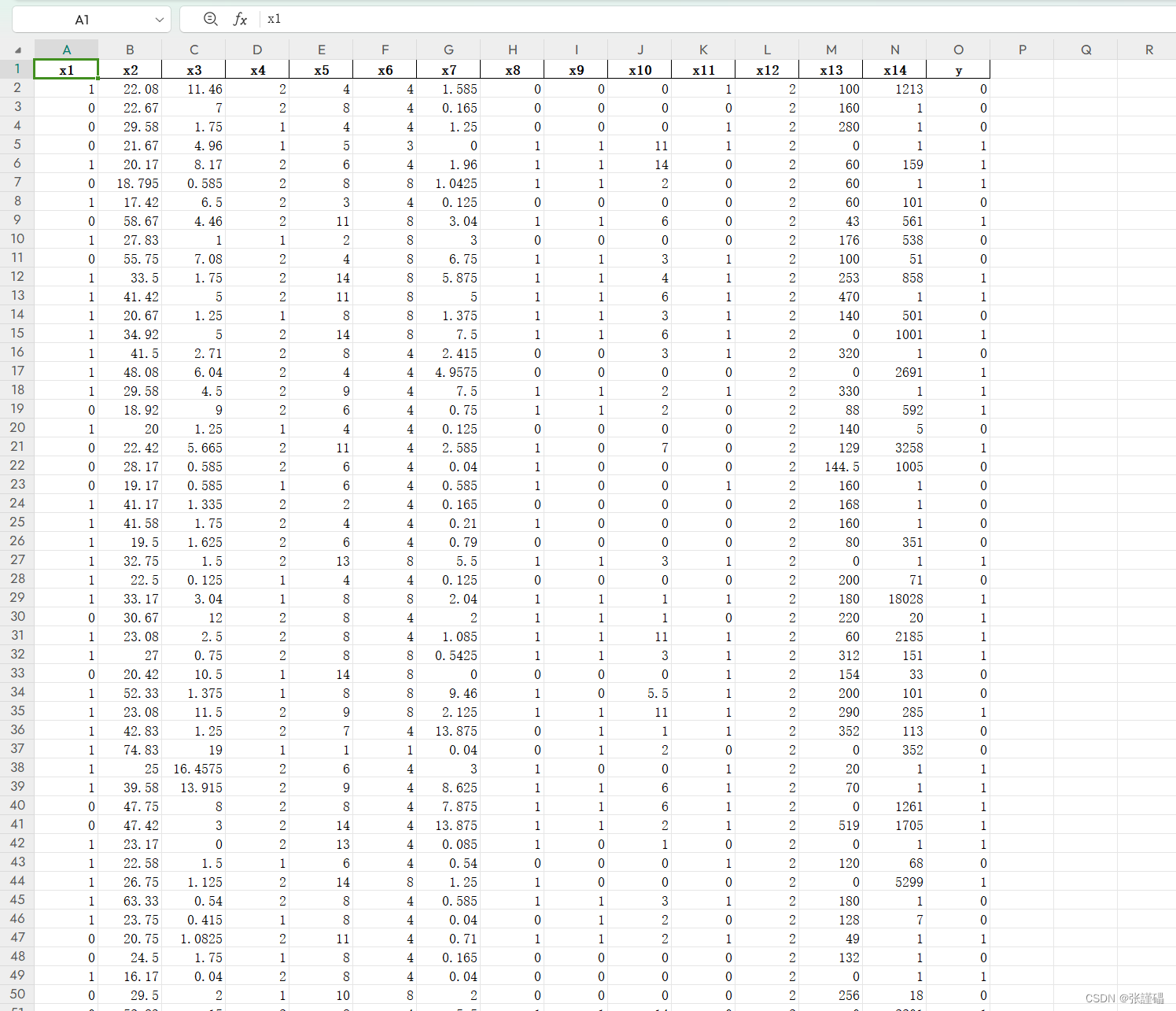

4. 基于模型预测填充

python复制代码

	from sklearn.experimental import enable_iterative_imputer
	from sklearn.impute import IterativeImputer
	# 迭代式填充
	imputer = IterativeImputer(max_iter=10, random_state=0)
	df_filled = imputer.fit_transform(df)
	df = pd.DataFrame(df_filled, columns=df.columns)

5. 热卡填充（示例代码，需要自定义逻辑）

import pandas as pd
from sklearn.impute import KNNImputer

# 读取Excel文件
df = pd.read_excel("银行贷款审批数据.xlsx")

# 假设 continuous_vars 是包含连续变量的列名的列表
continuous_vars = ['x2', 'x3', 'x5', 'x6', 'x7', 'x10', 'x13', 'x14']

# 提取连续变量
df_continuous = df[continuous_vars]

# 使用KNNImputer填充缺失值
# 设定K值，这里以2为例，你可以根据数据集的特性调整这个值
knn_imputer = KNNImputer(n_neighbors=2)
df_continuous_filled = knn_imputer.fit_transform(df_continuous)

# 将填充后的数据转换回DataFrame格式
df_continuous_filled = pd.DataFrame(df_continuous_filled, columns=continuous_vars)

# 将填充后的连续变量重新合并到原始DataFrame中
df[continuous_vars] = df_continuous_filled

# 检查是否还有缺失值
missing_values = df[continuous_vars].isnull().sum().sum()
if missing_values == 0:
    print("所有连续变量的缺失值已基于KNN填充。")
else:
    print(f"仍有 {missing_values} 个连续变量的缺失值未填充。")

# 保存填充后的数据框到Excel文件
df.to_excel("填充后的银行贷款审批数据_KNN填充.xlsx", index=False)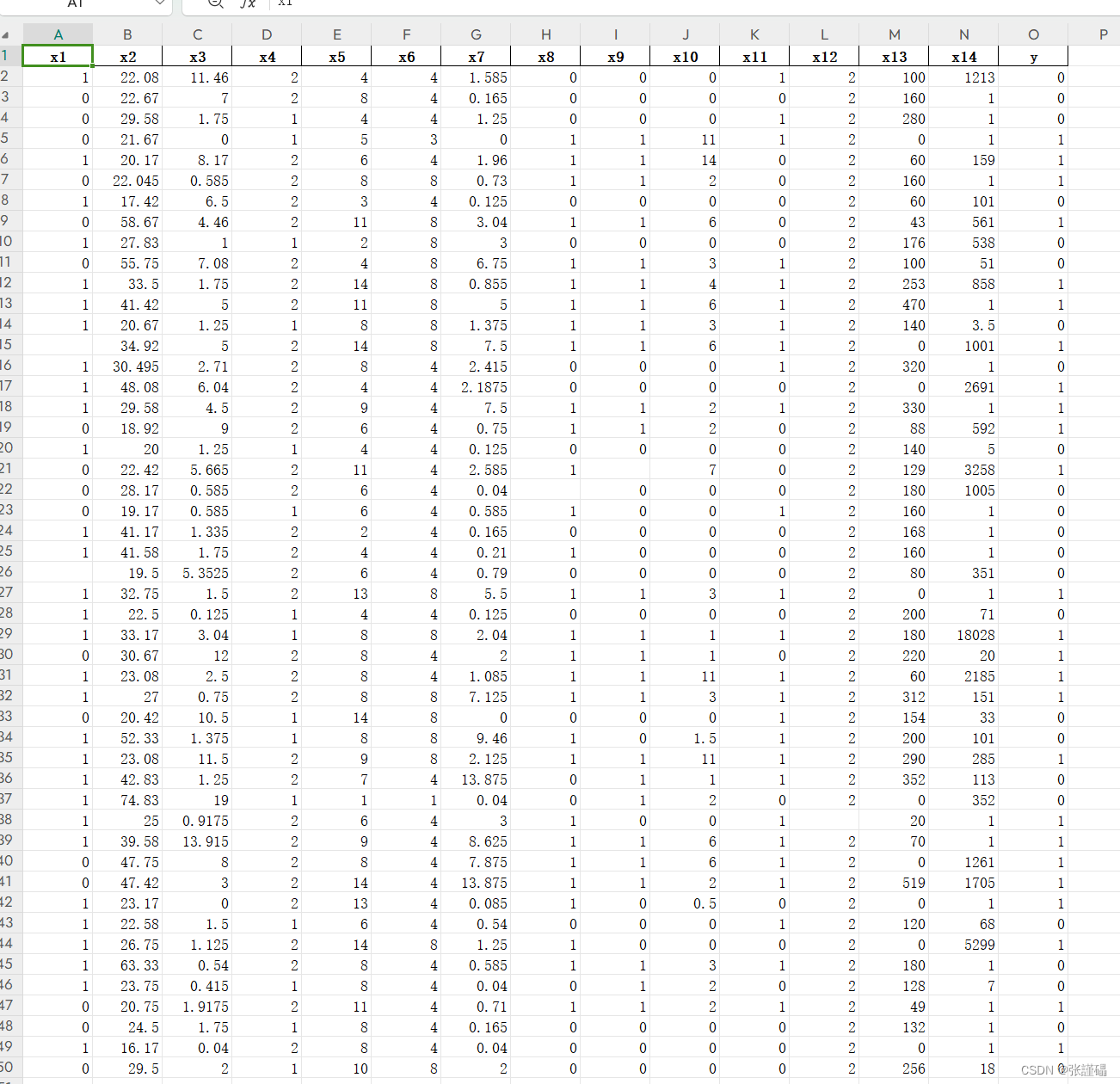

6. 多重插补（使用fancyimpute库）

import pandas as pd
from fancyimpute import IterativeImputer

# 读取Excel文件
df = pd.read_excel("银行贷款审批数据.xlsx")

# 初始化IterativeImputer
# max_iter设置迭代次数，可以设置较高的值以确保收敛
# min_value和max_value用于限制填充值的范围，可根据实际数据调整
imputer = IterativeImputer(max_iter=10, random_state=0, min_value=0, max_value=1)  # 假设数据在0和1之间

# 填充缺失值
df_filled = imputer.fit_transform(df)

# 将填充后的数组转换回DataFrame
df_filled = pd.DataFrame(df_filled, columns=df.columns)

# 检查是否还有缺失值
missing_values = df_filled.isnull().sum().sum()
if missing_values == 0:
    print("所有缺失值已基于多重插补填充。")
else:
    print(f"仍有 {missing_values} 个缺失值未填充。")

# 保存填充后的数据框到Excel文件
df_filled.to_excel("填充后的银行贷款审批数据_多重插补.xlsx", index=False)

7. 基于相似性的填充（使用K近邻）

python复制代码

	from sklearn.impute import KNNImputer
	# K近邻填充
	imputer = KNNImputer(n_neighbors=2)
	df_filled = imputer.fit_transform(df)
	df = pd.DataFrame(df_filled, columns=df.columns)

请注意，以上代码示例中的df['column_name']应替换为实际的列名，而df应替换为你的实际DataFrame。此外，某些方法可能需要额外的库，如scipy或fancyimpute，你可能需要先使用pip来安装它们。

每种填充方法都有其适用场景和局限性，选择哪种方法取决于数据的特性、缺失值的比例以及分析的目的。在实际应用中，可能需要尝试多种方法，并比较它们对分析结果的影响，以选择最合适的方法。